Je m'inspire souvent de vidéos de conférences d'universités américaines et allemandes, comme celles de l'Université Purdue, de l'Université de Californie, Berkeley, de l'Université de Stanford, du Massachusetts Institute of Technology (MIT), de Ohio University, de Indian Institute of Technology Delhi et de l'Université libre de Berlin (FU Berlin) parmi d'autres. Ils se caractérisent par leur clarté, leur qualité et leur approche pratique et orientée vers la recherche. Je vous recommande de regarder les vidéos proposées ici plutôt que de les chercher vous-même sur internet. C'est aussi une bonne occasion d'améliorer votre anglais


Aperçu de l'université virtuelle d'apprentissage
L'université virtuelle d'apprentissage (VLU) est une université en ligne à but non lucratif créée pendant la pandémie de COVID19 dans le but d'accroître l'accès à un enseignement supérieur et à une formation de qualité. Nous sommes un éventail de compétences de scientifiques de haut niveau hautement qualifiés avec un intérêt de longue date pour la recherche et l'enseignement dans les universités au Maroc, en Europe, et en Afrique du Nord . Nous explorons ce qui est décisif pour renforcer l'enseignement en prenant en considération la recherche et le développement (R&D) comme base pour l'apprentissage. Notre objective est d´apporter des améliorations et des innovations significatives à notre système éducatif. Nous ciblons les étudiants marocains et nous étendons notre expérience à l'Afrique et au Moyen-Orient. Nous nous concentrons sur l'accès à l'enseignement supérieur et à la formation continue dans les domaines suivants : énergies renouvelables et stockage de l'énergie, contrôle de la pollution de l'air et de l'eau, traitement et gestion des déchets, la biodiversité, le changement climatique les sciences de l'environnement, l´ingénierie géologique et le développement durable.
Nous sommes prêts à développer un partenariat mutuellement bénéfique entre VLU et d'autres établissements d'enseignement. Nous avons la chance de pouvoir établir des partenariats et des réseaux efficaces avec plusieurs organisations marocaines et étrangères. Notre feuille de route vise à développer des programmes pour l'excellence académique et l'innovation dans les sciences et techniques (S&T), offrant des possibilités d'obtenir des certificats reconnus. Nous sommes prêts à négocier avec des universités marocaines et internationales pour que nos diplômes d'enseignement soient reconnus et acceptés Maroc et à l'étranger.
Notre objectifs et méthodes d'enseignement consists à travailler avec les jeunes et mettre en pratique les connaissances scientifiques dans le cadre du développement durable autour de la qualité de l'air, de l'eau et une faible empreinte carbone dans l'industrie. En fait, les apprenants et les instructeurs interagissent en utilisant des systèmes informatiques, les présentations d'études de cas, des exercices pratiques.
Les outils de formation sont des manuels - Guide d'étude, feuilles de travail, polycopiés de cours en ligne, enregistrements videos de conférences ; logiciels et outils de simulation pertinents ; apprentissage interactif, films/vidéos


AHMED ENNAOUI
Président du conseil scientifique de l'IRESEN. Ancien chef de groupe de recherche au Helmholtz-Zentrum Berlin für, Materialien und Energie et fondateur de l'Université Virtuelle d'Apprentissage
dr.ahmed.ennaoui@ieee.org
Bio - Ahmed Ennaoui a obtenu son diplôme des études approfondies (DEA) et sa thèse de doctorat en électronique de l'état solide à l'université de Bourgogne, en France. Il a commencé sa carrière comme professeur associé en 1979 à l'Université Mohamed V. Il intégre l'Institut Hahn-Meitner de Berlin (HMI) en 1983 en tant que scientifique effectuant des recherches pour son habilitation. En avril 1987, il a défendu et obtenu son habilitation (summa cum laude) sur de nouveaux matériaux abondants pour la conversion de l'énergie solaire. Il est ensuite noté pour diriger un groupe de recherche à l'Institut des systèmes de matériaux hétérogènes au Helmholtz-Zentrum Berlin (HZB) pour les matériaux et l'énergie, et a aussi participé à l'évaluation du programme de séminaire sur les énergies renouvelables pour les étudiants de troisième cycle à l'université libre de Berlin. Il a été invité par Prof. Matsumura au Centre de recherche sur la chimie de l'énergie solaire de l'université d'Osaka, au Japon. Il a servi comme directeur de recherche à l'Institut de recherche sur l'environnement et l'énergie du Qatar (QEERI) et comme professeur à l'Université Hamad Bin Khalifa. Les publications de M. Ennaoui portent principalement sur les chalcogénures de métaux de transition, les composés binaires et ternaires en couches minces et les cellules solaires basées sur ces matériaux. Il a mené des recherches sur les cellules solaires à couches minces imprimées par jet d'encre et sur les solutions d'encrassement des panneaux photovoltaïques. Il a publié plus de 300 contributions scientifiques, y compris des articles de recherche évalués par des pairs et de nombreuses conférences invitées. Récemment, il a été classé par l'université de Stanford parmi les 2 % de chercheurs les plus performants au monde sur les 224 856 chercheurs en physique appliquée recensés par la prestigieuse université américaine, selon l'AD Scientific Index. Il est membre permanent du comité de rédaction du journal Solar Energy Materials and Solar Cells, membre de "International Energy Society (ISES)" et "senior member" de l'Institute of Electrical and Electronic Engineers (IEEE). Au cours de sa carrière, il a supervisé plusieurs thèses et habilitations, et plusieurs postdoctorants ont travaillé dans son groupe. Professeur Ennaoui est actuellement président du conseil scientifique de l'Institut de l'énergie solaire et des énergies nouvelles (IRESEN), il a contribue au développement des énergies renouvelables en suivant l'achèvement des projets de recherche et de développement de IRESEN tout en organisant et en participant à plusieurs conférences internationales au Maroc et dans le monde sur les énergies vertes. Il est le fondateur de cette université virtuelle d'apprentissage
I'm very grateful to my colleagues for the kindness, and for the generosity they show in giving their time and support to the Virtual Learning University












Dip- Ing. Badr Ikken
Président exécutif de Gi3 / Associé gérant de Gi2 / Président du Conseil d'affaires Maroc-Allemagne - CGEM Membre du Conseil d'administration de la Chambre de commerce allemande AHK Maroc
Prof. Abdelilah Benyoussef
Académie Hassan II des Sciences et Technologies, Rabat, Maroc LaMCScI, Faculté des Sciences, Université Mohammed V, Rabat, Maroc
Ostad Salem Rajab Zayed Omar
Directeur exécutif de Sabaek pour l'éducation et la formation, les programmes sociaux, le développement humain, (Royaume de Bahreïn)
Dr. Ismail Akalay
Directeur général de Sonasid et ancien directeur général du cobalt et des métaux de base Directeur général du cobalt et des métaux de base
Prof. Ismael Saadoune
Professeur titulaire à l'Université polytechnique Mohammed VI, Maroc. Expert en stockage électrochimique de l'énergie et en recyclage des batteries.
Assoc. Prof. Saleh Khamlich
Centre de recherche d'excellence, UM6P - Université polytechnique Mohammed VI


Prof. Ahmed Ihlal
Université Ibn Zohr, Faculté des Sciences,
served as expert évaluateur dans le domaine des énergies renouvelables pour le CNRST
De la physique de newton à la physique statistique quantique et la physique des cellules solaires
Introduction - Les lois de la physique étudient l'interaction de deux particules et peuvent être schématisées de la façon suivante:
Les lois de la mécanique classique qui déterminent la trajectoire d'une particule soumise à l'action d'une autre particule à partir du principe de Newton:
Le paramètre temps (t), joue un rôle particulier. L'évolution de la particule est décrite par la donnée de sa trajectoire dans l'espace de phase: un espace à six dimensions {q ⃗(t) ; p ⃗(t)} qui sont les coordonnées et les impulsions généralisées de la particule. L'interaction entre deux particules chargées en mouvement n'est pas régie par (1) mais par la donnée des les équations de Maxwell en unité MKSA rationalisées
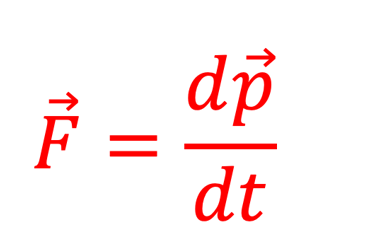
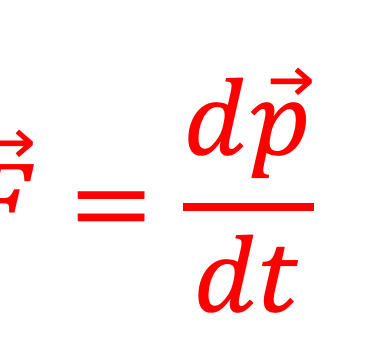



La force que subit la charge élémentaire dans le champ (E ⃗ ; B ⃗ ) est celle de Lorenz:
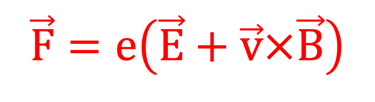
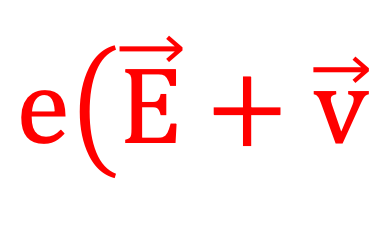
où v ⃗ est la vitesse de la particule de charge e
L'invariance des équations de Maxwell par les transformations de Lorenz montre que le temps ne joue plus le rôle d'un paramètre indépendant mais devient la quatrième coordonnées: c'est l'espace quadridimensionnel de Minkowski, la relativité restreinte et la mécanique relativiste
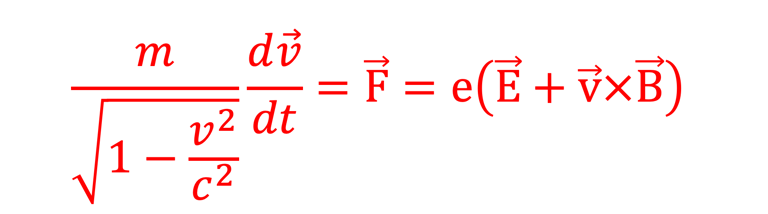
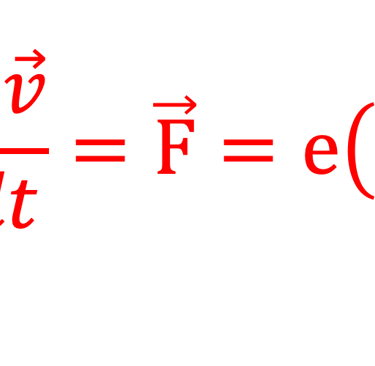
(4) admet la mécanique Newtonienne comme limite toutes les fois où les vitesse des particules interagissant sont faibles devant la vitesse de la lumière (v << c)
Par ailleurs, la particule microscopique n'obéit pas à l'équation de Newton (1) mais à celle de Schrödinger
(1)
(2)
(3)
(4)
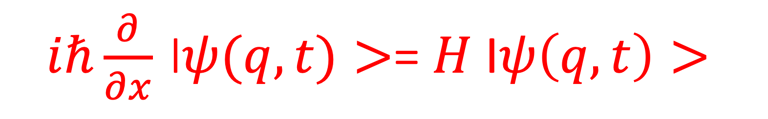
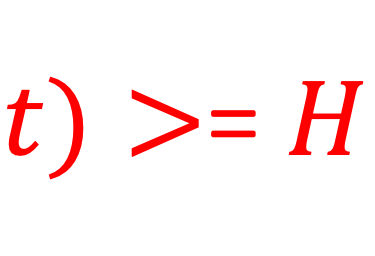
(5)
où H est l'opérateur Hamiltonien et Iψ(q,t)> un vecteur appartenant à l'espace de Hilbert: c'est la mécanique quantique, la science de l'infiniment petit qui permet d'expliquer et interprèter le comportement de la matière, et ses interactions avec l'énergie de la lumière, à l'échelle des atomes et des particules subatomiques.
L'absence de trajectoire, ou l'impossibilité de mesurer simultanément la position q(t) et la quantité de mouvement p(t) de la particule, nous amène à faire correspondre à chaque grandeur physique {q(t) ; p(t)}un opérateur correspondant {"Q ; P" } agissant sur les vecteurs de l'espace de Hilbert et à définir par conséquent les relations de commutation entre opérateurs
Notons que le fait que la position et la quantité de mouvement ne commutent pas directement conduit au principe d'incertitude et au fait qu'elles sont des transformées de Fourier l'une de l'autre.
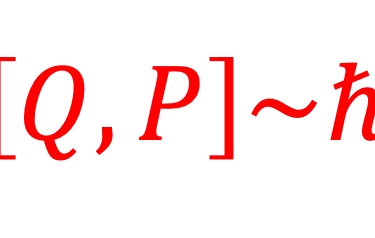
(6)
ou ℏ = h/2π et h est la constante de Planck, 0,00000000000000000000000000000000006626 joule . seconde
Il ne pouvait y avoir de degré inférieur à h dans l'augmentation ou la diminution de l'énergie, mais la valeur infinitésimale de h rend les effets quantiques invisibles dans l'univers quotidien quand il s'agit de pendules, de balançoires et de poids vibrants [cette phrase extraite du livre Le grand roman de la physique quantique par Manjit Kumar traduit de l'anglais par Bernard Sigaud ]
Q et P sont des observables correspondant respectivement aux grandeurs mesurables p et q
L'équation de Schrödinger en tant qu'équation d'onde obéissant à des conditions aux limites, et la solution de l'équation aux valeurs propres
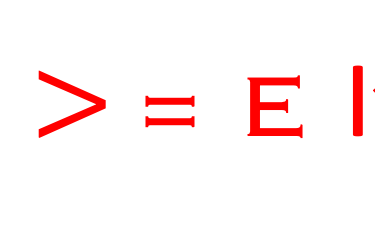
(7)
L'opérateur H est indépendant du temps, et les grandeurs physiques, telle que les énergies E par exemple - ont des valeurs discrètes, et c'est ce passage du continu au discret qui caractérise la mécanique quantique.
Nous retrouvons la mécanique classique - les trajectoires - toutes les fois où (6) est nulle c'est à dire toutes les fois où l'on peut négliger les actions de l'ordre de ℏ. Ainsi les grandeurs physiques perdent leur qualité d'opérateur
Les particules microscopiques très rapide doivent être décrites par la mécanique quantique et la relativité restreinte: c'est la théorie quantique des champs.
Pour les photons par exemple, l'équation d'onde déduite des équations de Maxwell avec (E ⃗ ; B ⃗ ) ou le quadrivecteur potentiel (v ⃗ ; A ⃗ ) devenant opérateur,
Toutes ces lois, répétons-le, ne concernent que l’évolution d'une particule dans le champ d'une autre particule: problème à deux corps. La solution des équations se complique considérablement dès que l'on passe à l'interaction entre trois corps, et N corps. C'est l'objective de la mécanique statistique, qui permet d´étudier les propriés macroscopiques d'un système en équilibre à partir de la connaissance des propriétés microscopiques en utilisant la loi de la mécanique
L'idée fondamentale c´est que la probabilité ou le poids statistique d'un état macroscopique particulier dépend du nombre de façons possibles dont cet état peut être construit à partir de ses constituants microscopiques
Grâce à la statistique de Bose-Einstein (B-E), il est possible de décrire le champ de rayonnement à l'intérieur d'un corps noir et les phénomènes collectifs associés à la condensation d'un système macroscopique dans son état quantique le plus bas,
Les statistiques de Fermi-Dirac (F-D) permettent de mieux comprendre comment les propriétés électroniques des métaux et des semi-conducteurs sont liées aux propriétés dynamiques de leurs porteurs de charge.
La mécanique quantique avec sa constante fondamentale qui est l'action (h) et la physique statistique avec sa constante (kB), la constante de Boltzmann, qui permet de relier température absolue (T) et énergie par degré de liberté E ∼ kB . T sont deux domaines essentiels de la physique moderne qui ont permet le développements des science des matériaux où l´approche classique est inadaptée pour décrire expérimentalement les phénomènes physiques. Nous avons l'occasion d'utiliser concepts fondamentaux de la mécanique quantique et physique statistique pour décrire les électrons dans les matériaux semi-conducteurs et composants électroniques tels que les cellules solaires
Nous souhaitons que les visiteurs de ce site puisse atteindre les objectify suivant
(1) Faire preuve d'un haut niveau d'érudition et d'intégrité académique
(2) Acquérir et démontrer la capacité d'examiner et d'évaluer de manière critique la littérature scientifique
(3) Démontrer des compétences efficaces en matière de communication scientifique et universitaire dans le cadre de présentations écrites et orales et d'autres formes de publications
(4) Démontrer la capacité à générer des idées nouvelles et à mener des recherches scientifiques indépendantes pour faire progresser l'ensemble des connaissances et/ou des technologies au profit de la société, de la nation et de l'humanité
(5) Atteindre un niveau exceptionnel de connaissances sur les questions fondamentales de durabilité en matière d'environnement, de technologie, d'énergie, de politique et d’économie
(6) Acquérir une compréhension fondamentale des outils d'évaluation et d'analyse de la durabilité et les améliorer en permanence ;
(7) Développer une compréhension approfondie de la dynamique des questions multiformes et interdépendantes de l'économie, de l'environnement, de l'énergie, de l'agriculture, de l'eau, de l'alimentation, de l'urbanisation et de l'élaboration des politiques afin d'aborder efficacement les questions émergentes en matière de développement durable autour des ressources naturelles (environnement, utilisation et qualité de l'air, de l'eau et du sol ; émissions industrielles et urbaines) et de l'utilisation de ces ressources en mettant l'accent sur l'efficacité, la valeur du cycle de vie, l'impact sur la société future, l'énergie et l'économie
(8) Acquérir et démontrer un haut niveau de compréhension des processus naturels de transport, d'accumulation, de croissance et de biodégradation dans l'environnement et de l'impact des activités humaines sur ces processus ;
(9) Acquérir et démontrer une compréhension progressive des technologies et méthodes de pointe en matière de surveillance, de protection et d'assainissement de l'environnement, ainsi que des besoins énergétiques, des considérations économiques et des risques qui y sont associés ;
(10) Acquérir les connaissances et les compétences nécessaires pour prendre des décisions sur les technologies de traitement de l'eau pour le dessalement, le traitement traditionnel de l'eau, le traitement des eaux usées et les systèmes de réutilisation de l'eau.
(11) Acquérir et démontrer un haut niveau de compréhension et de connaissance des différents écosystèmes et des relations entre la santé humaine et la qualité de l'environnement.
(12) Acquérir une compréhension fondamentale de la dynamique actuelle et future des ressources en eau, y compris leur sécurité, leur qualité, leur localisation, les exigences en matière de purification et les droits d'accès.
(13) Acquérir une compréhension fondamentale des moteurs sociaux et économiques et des réponses à la conservation et à l'efficacité des ressources.
(14) Démontrer la capacité d'observer et de comprendre les besoins à court et à long terme de leur société immédiate et plus large et de générer des solutions, des produits, des processus et/ou des modèles technologiques et/ou sociaux innovants au profit de la société pour son développement économique, social et environnemental ; Acquérir des compétences tout au long de la vie en matière d'analyse de données ; d'environnements, de compétences et d'outils de méthodes informatiques avancées ; et de méthodes de recherche, de propriété intellectuelle et d'éthique.
Cours #I : Introduction à l'électronique des matériaux
Ce cours est très utile pour comprendre le fonctionnement des dispositifs d'absorption et/ou d'émission de lumière à base de semi-conducteurs, tels que les cellules solaires, les détecteurs, les lasers à semi-conducteurs, etc.. Il s'adresse principalement aux étudiants de bachelor et de master, mais aussi à ceux qui sont plus avancés dans leur travail de doctorat en génie des matériaux électriques/électroniques. Dans la mesure du possible, nous utiliserons un traitement mathématique très simple avec l'intuition d'un physicien et d'un physico-chimiste. Nous utiliserons la physique de la matière condensée, la mécanique statistique, la thermodynamique et la science des matériaux dans une perspective d'ingénierie pour le développement de cellules solaires, le stockage de l'énergie, la production d'hydrogène vert et d'autres domaines de recherche et développement
Cours #I: Thèmes abordés :
Spectres d'émission atomique, atomes, molécules, liaisons interatomiques, niveaux d'énergie des atomes, niveaux d'énergie des bandes, dualité onde-particule, cellule unitaire, solides cristallins, directions cristallographiques, équation de Bragg, indices de Miller <h, k, l>, détermination des paramètres du réseau, énergie et quantité de mouvement des électrons, densité d'états (DOS), classification des matériaux : Métal, isolant, semi-conducteur, Remplissage des états électroniques, Semi-conducteurs et bande interdite, Electrons et trous, Niveau de Fermi, bande interdite directe et indirecte, Courants de dérive et de diffusion, mobilité (μn) des électrons libres et (μp) des trous libres, DOS dans la bande de conduction (CB), DOS dans la bande de valence (VB), Introduction à la technologie du silicium et Evolution de l'industrie photovoltaïque au silicium du point de vue de l'innovation technologique.


I.1 - Spectres d'émission atomique et niveaux d'énergie
Le spectre d’émission de l’atome d’hydrogène, a été exploré par Niels Bohr en 1913 proposant un modèle d'un atome et un électron qui tourne autour du noyau de cet atome avec des moments cinétiques (vitesses) multiples d'une constante (la constante de Plank). Ainsi l´électron passe d’un niveau d´énergie En+1 vers un niveau En de plus basse énergie tout en émettant un photon. Inversement Bohr propose qu’un électron passe vers un niveau excité par absorption d’un photon lorsque son énergie est suffisante.
Trois postulats en découle de cette hypothèse:
(1) À l’échelle atomique un système ne peut exister que dans des états stationnaires spécifiques. on appelle cela "Quantification" du moment cinétique
Comme le moments cinétiques est relié à l´énergie c'est la "Quantification" de l´énergie qui ne peut prendre que des valeurs discrètes, qui définissent les niveaux d’énergie
(2) Lorsque le système change d´ état stationnaire de haute énergie vers un état stationnaire et passe d'un état d´énergie En+1 vers un état d´énergie En plus basse il émet (spectre d´émission) un photon de fréquence bien déterminée donnée par la relation:
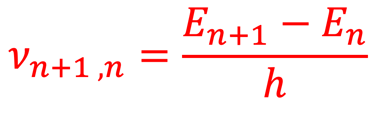
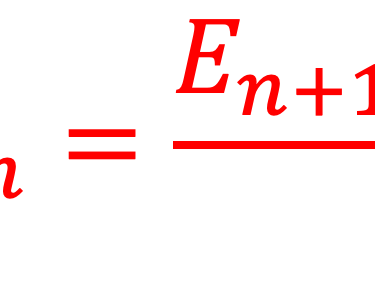
(3) Le phénomène inverse peut se produire, et un système peut passer d'un niveau d´énergie En vers un niveau d´énergie En+1 par absorption d’un photon (spectre d'absorption). La valeur de cette energie est égale à l’écart d’énergie entre les deux niveaux
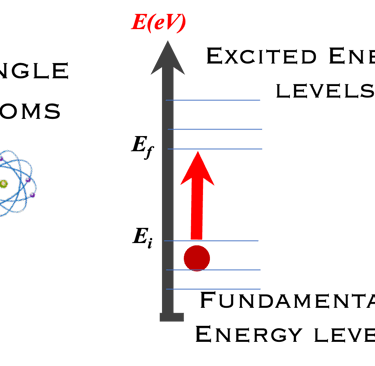
Le schèma ci-dessous illustre les niveau d'énergie d'un atome ainsi que le phénomène d´absorption et d´émission
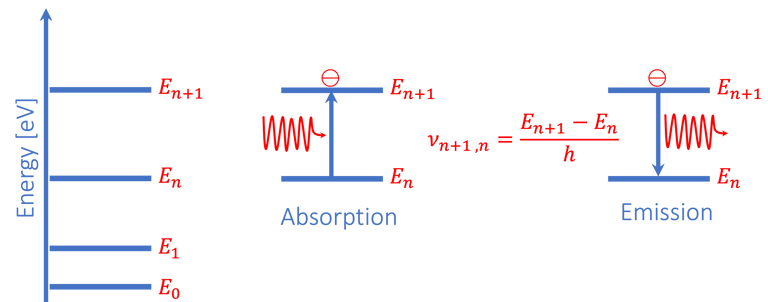
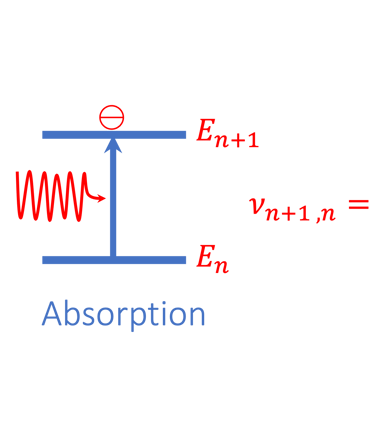
Schema à gauche, montrant les niveaux d´énergie d'un atome. Au milieu l'absorption d'un photon d'un état En à un état excité instable. à droite l’électron redescend à son niveau d’énergie initiale en restituant son énergie sous la forme d’un photon. On peut mesurer à l'aide d'un spectromètre le spectre d'émission de la lumière qui caractérise le système
L'exemple ci-dessous montre le schéma d´une lampe à vapeur de mercure (Hg) et le phénomène d'absorption et d´émission. La tension appliquée permet un flux d'électrons de se produire, il en résulte des collisions avec les électrons de l'atome de Hg, les électrons passent à un niveau d'énergie supérieur et se désexcitent en générant des photons dans la gamme des ultraviolets (UV). L´intérieur du tube étant revêtu d'un matériau fluorescent reçoivent ces photons UV, ils sont à leur tour excités et désexcités en émettant de la lumière visible.
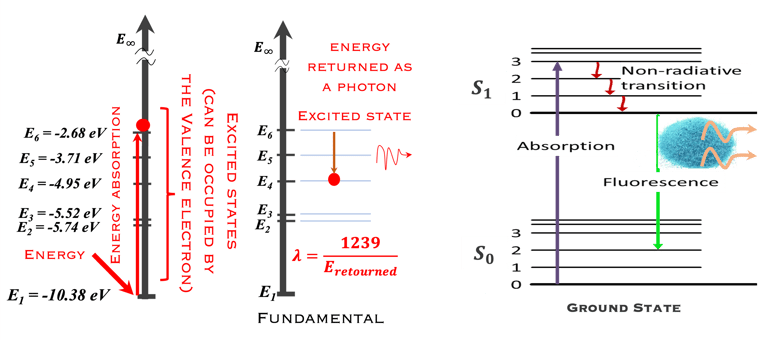
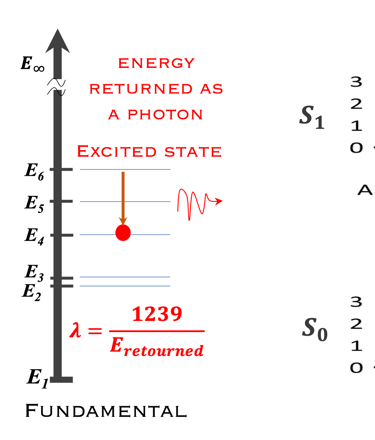
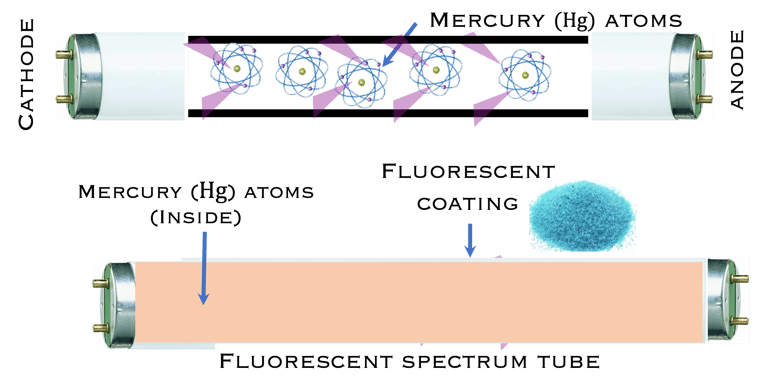
Les atomes de l'état solide S0 absorbent les UV, les électrons se déplacent vers les états excités S1. En retournant à l'état fondamental stable des photons (fluorescence) sont émis dans le visible
Table à vapeur de Hg, vêtu d'un matériau fluorescent
Lorsqu'un atome est exposé à une source d'énergie, ses électrons absorbent une énergie spécifique caractéristique de l'atome.
L'énergie absorbée permet aux électrons de passer de l'état initial Ei à un niveau d'énergie plus élevé (appelé état excité, Ef).
Les électrons sont instables dans l'état excité Ef et se détendent naturellement vers l'état fondamental E0.
Une particule appelée « photon » d'énergie ℎ𝜈 = ℎ𝑐/𝜆 est émise.
C'est ce qui se passe dans les tubes à décharge de mercure (Hg)
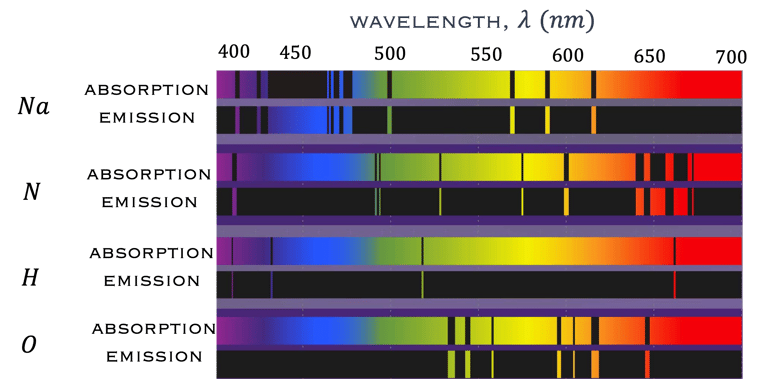
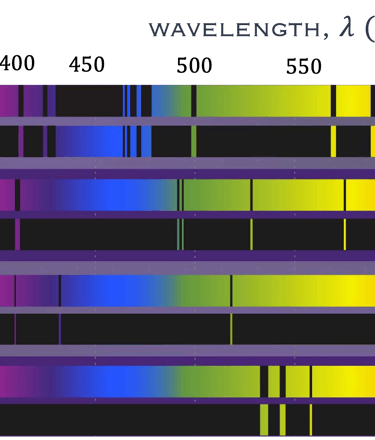
Les raies spectrales atomiques sont la signature de l'élément en fonction de sa configuration électronique.
Introduction à la Cristallographie
Regarder les videos



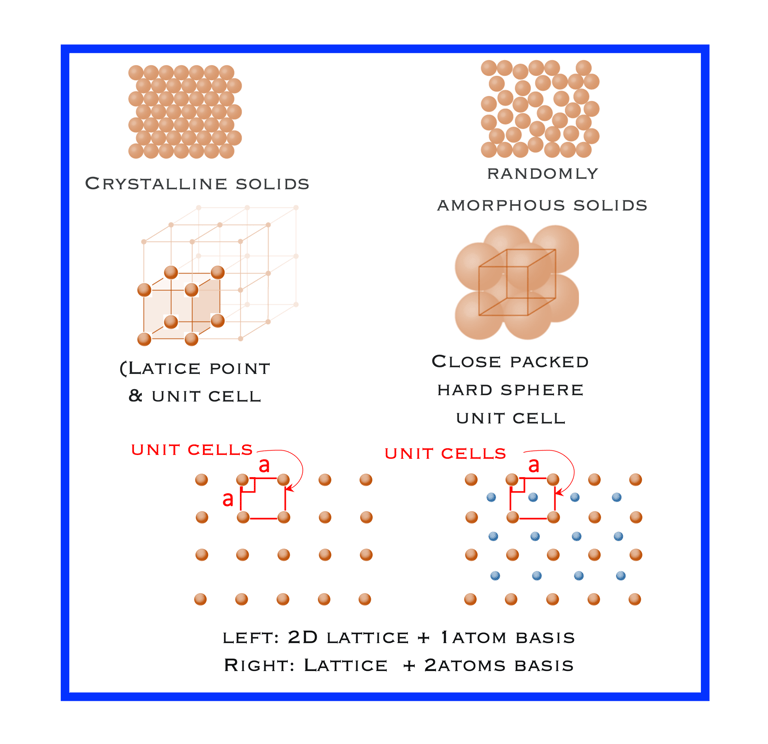
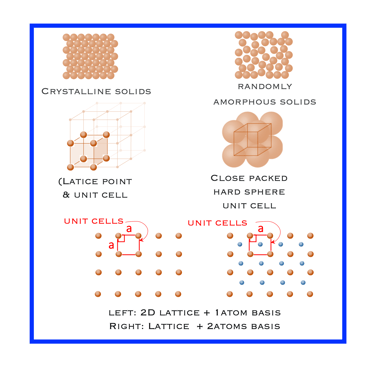
Solides cristallins - les particules (atomes) sont liées les unes aux autres de façon régulière pour former un réseau périodique de particules, contrairement aux structures amorphes où les atomes ou les molécules ne sont pas disposés dans un ordre régulier et répétitif,
Structure cristalline - elle est subdivisée en petites répétitions, appelées "cellules unitaires"
Cellules unitaires - sont les éléments de base de la structure cristalline et représentent la symétrie de la structure cristalline
Construction en 2D d'une cellule de Wigner-Seitz
Choisissez n'importe quel point du réseau
Tracez des lignes de connexion vers les voisins les plus proches.
Construit les bissectrices perpendiculaires des lignes de connexion.
La zone délimitée est la cellule de Wigner-Seitz, elle constitue une cellule unitaire pour la construction du réseau entier
Nous allons examiner 3 structures cristallines courantes
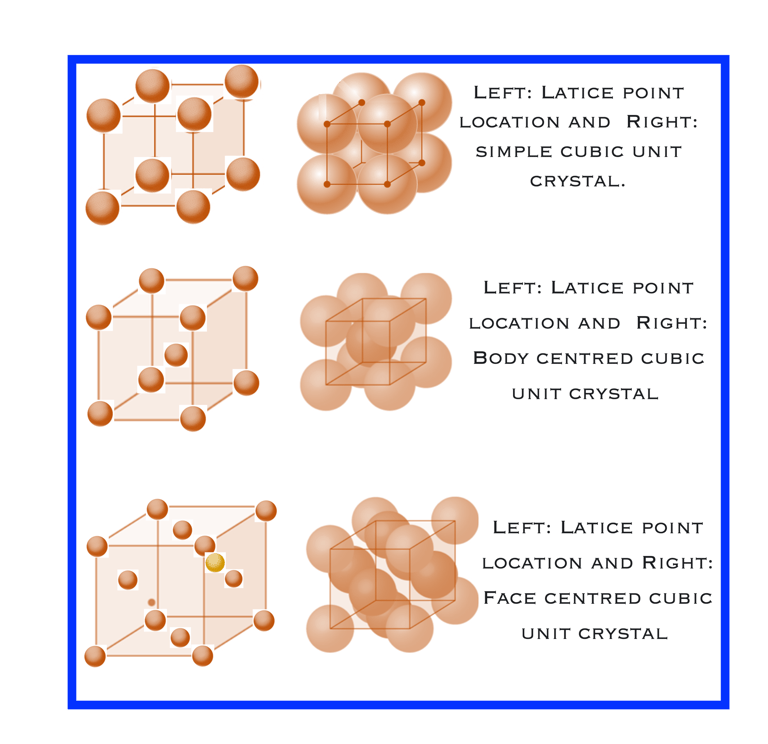
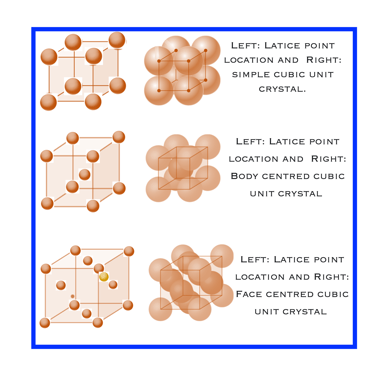
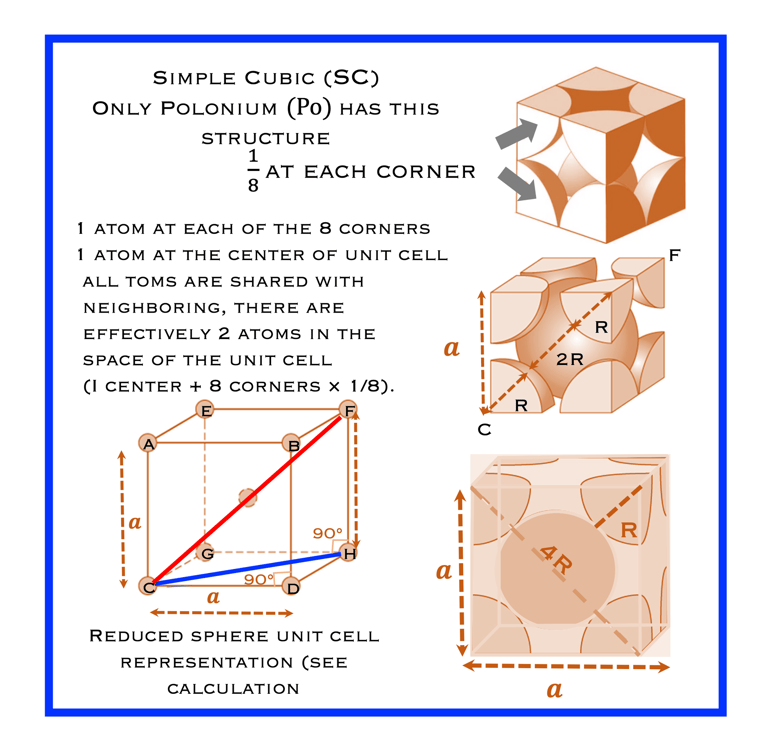
Structure cubique simple: La cellule unitaire a 1 atome à chacun de ses huit « coins », soit 8×1/8=1 atome dans une cellule unitaire cubique simple
Cubique centré (Body-Centered Cubic, BCC) : La cellule unitaire est constituée de 1/8 d'atome à chacun des 8 coins. (i.e. 8×1/8=1) plus 1 atome au centre
Cubique à faces centrées (Face Centered Cubic, FCC) : Chaque atome touche 12 voisins proches: 3 couches répétées disposées de manière hexagonale. Chaque atome entre en contact avec 6 atomes dans sa propre couche, 3 dans la couche supérieure et 3 dans la couche inférieure
QUIZ:
Trouvez le nombre de coordination : # Nombre de voisins les plus proches d'un atome dans la cellule unitaire d'une structure cristalline.
Coordination cubique simple (SC) # = 6
Coordination cubique centrée (corps) (BCC) # = 8
Coordination cubique centrée (face) (FCC) # = 1
La structure cristalline métallique typique (par exemple la phase α de Fe, Cr, W, Ta, Mo,...) avec les 8 coins et le centre de la cellule unitaire occupés, connue sous le nom de structure cristalline cubique centrée (BCC), est représentée par un modèle de sphère dure et réduite, les atomes du centre et des coins se touchant l'un l'autre le long de la diagonale du cube. Montrez que le paramètre a de la cellule unitaire et le rayon sont liés par la relation suivante
QUIZ:
Explorer les coordonnées de points pour une cellules unitaire BCC (résultats dans le tableau)
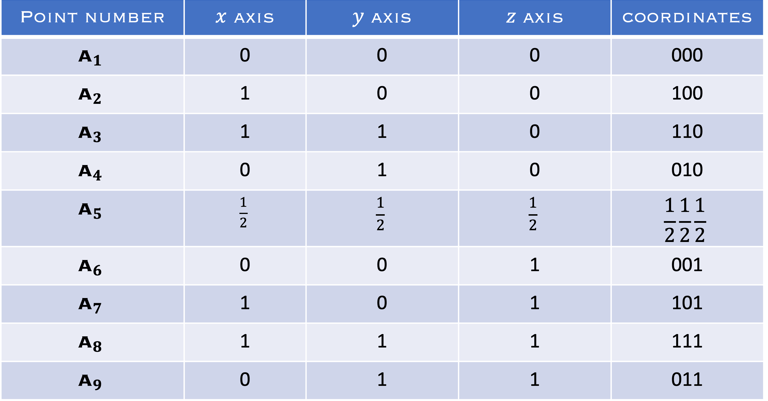
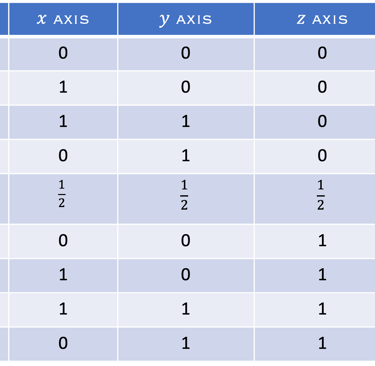
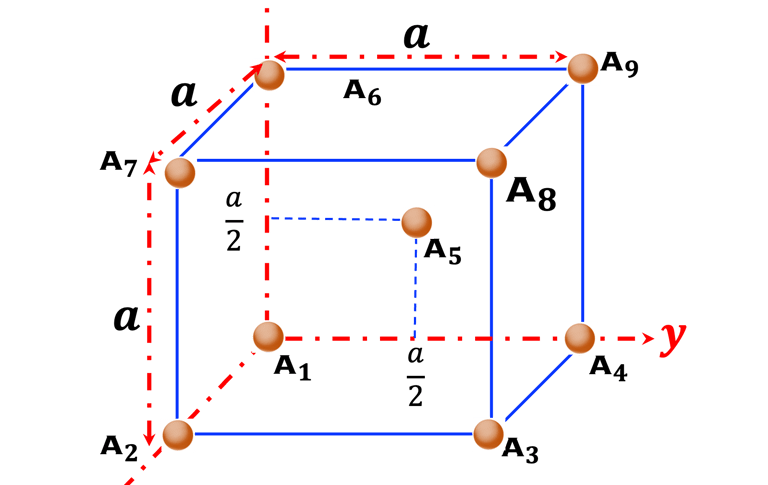
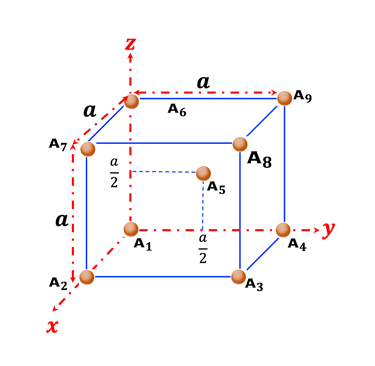
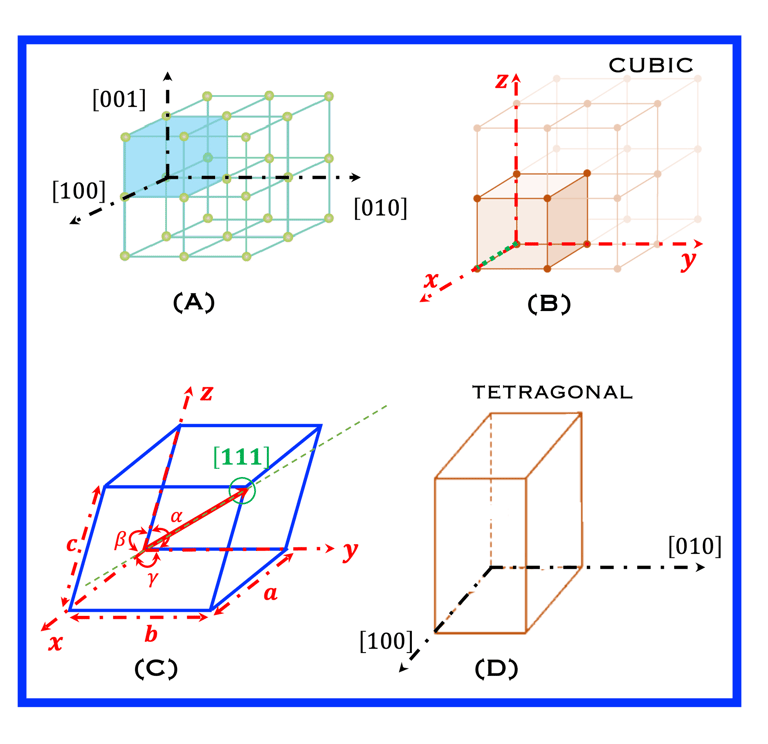
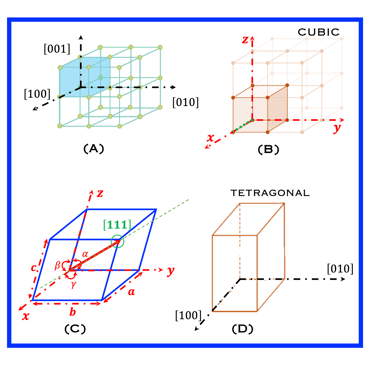
Explorer dans les illustration suivantes
La cellule unitaire ou la plus petite unité de construction de la structure cristalline
L'ensemble du réseau est généré par la répétition de la cellule unitaire dans différentes directions.
Les paramètres d'une cellule unitaire sont au nombre de six : 3 arêtes a, b, c et les angles entre les arêtes qui sont α, β, γ
Les bords d'une cellule unitaire ne sont pas nécessairement perpendiculaires les uns aux autres.
Détermination de la direction cristallographique :
1. Choisir un point comme origine
2. Déterminer les valeurs de l'autre point en terme de a, b, c
3. Écrire les 3 valeurs entre crochets (exemple(illustration C) [111])
Explorer les indices de Miller pour les directions et les plans
On note indices les indices de Miller [u v w] pour les directions et (h k l) pour les plans
u, v et w sont les cordonnées d’un vecteur reliant l’origine O (0,0,0) du repère oxyz avec un autre point qui se trouve sur la surface de la maille
h, k et l sont les inverses des longueurs découpées sur les axes ox, oy et oz respectivement par un plan noté (hkl)
Pour les plans parallèles qui ne diffèrent que par un décalage de translation, les mêmes indices de Miller peuvent être attribués à ces plans
Dans l'illustration (à droite), le plan vert (010) coupe l'axe des y en b
Si nous déplaçons le plan le long de y de deux paramètres du réseau (2b), il coupera l'axe y à 2b et les indices de Miller deviendront (010).
Les plans séparés par un multiple entier du paramètre du réseau ont les mêmes indices de Miller.
Pour un nombre entier négatif dû à une ordonnée à l'origine négative, une barre est placée en travers du sommet du nombre entier, comme par exemple :
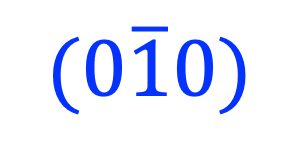
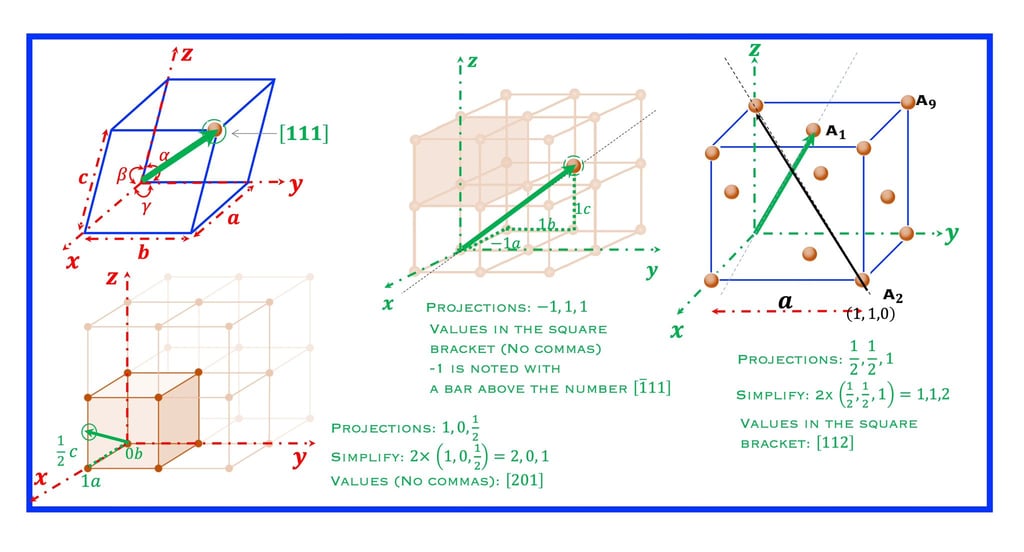
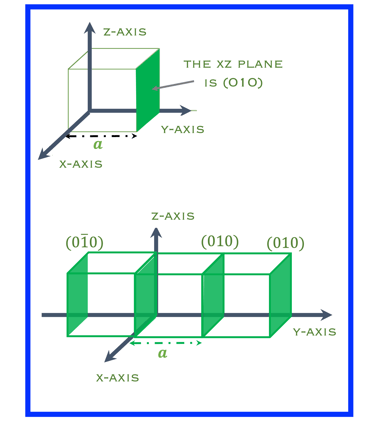
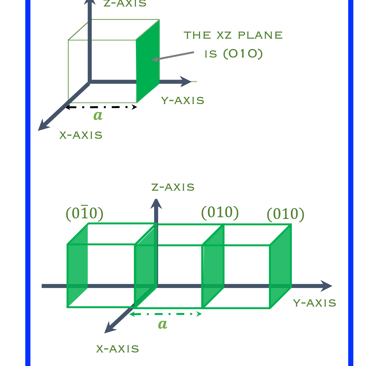
EQUIZ: Trouver les indices de Miller des plans colorés
Un plan cristallographique est spécifié en termes de longueur de ses intercepts sur trois axes
(1) le plan coupe l'axe des y à 1b
L'axe des x et l'axe des z étant parallèles au plan, la coupe des deux axes se fait à l'infini ∞
L'ordonnée à l'origine des axes est (∞,1,∞) , et L'ordonnée à l'origine réciproque : (1/∞,1/1,1/∞) = hkl= <010>.
(2) le plan coupe l'axe y à 1a
Les axes y et z étant parallèles au plan, la coupure des deux axes se fait à l'infini ∞
L'ordonnée à l'origine est (1,∞, ∞) , et L'ordonnée à l'origine réciproque : (1/1, 1/∞,1/∞) = hkl= <100>
(3) le plan coupe l'axe des y à 1c
Comme les axes x et y sont parallèles au plan, la coupure des deux axes se fait à l'infini ∞.
L'ordonnée à l'origine des axes est (∞, ∞,1) , et L'entier réciproque :(1/1, 1/∞,1/∞) = hkl= <001>
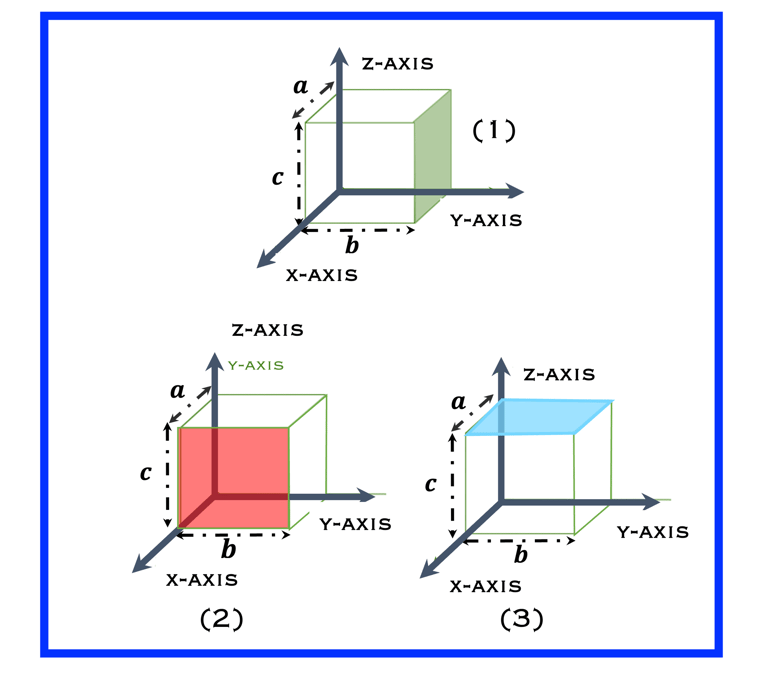
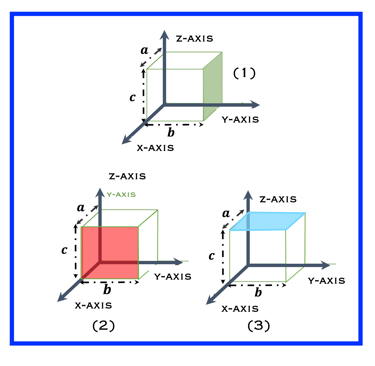
Testez vos connaissances: La cellule cubique a 12 arêtes, 8 coins, 6 faces et 1 centre, où un atome occupe une fraction du volume de la cellule. Il existe trois principaux types de cellules cubiques :
cubique primitive
cubique centrée sur le corps (BCC)
cubique centrée sur la face (FCC)
Chacune a une disposition différente des atomes et la masse d'une unité peut être calculée à partir du nombre total d'atomes à l'intérieur de la cellule
Exemple: Cas de l'atome de Cu: chaque coin est partagé avec huit autres cellules unitaires adjacentes
Chaque atome de Cu au centre de la face est partagé avec la cellule voisine
Le nombre d'atomes dans la cellule = 8 coins (1/8 atome) + 6 faces (1/2 atome) = 4 atomes
QUIZ: Considérons le cristal de cuivre avec la cellule unitaire FCC illustrée dans la figure
Combien y a-t-il d'atomes par cellule unitaire ?
R est le rayon de l'atome de Cu, montrez que le paramètre de réseau a est donné par 𝑎 = 𝑅 2√2
Calculer l'APF (Atomic Packing Factor)
Calculer la concentration atomique (nombre d'atomes par unité de volume) et la densité du cristal sachant que la masse atomique du cuivre est de 63,55 g/mol et que le rayon de l'atome de Cu est de 0,128 𝑛𝑚
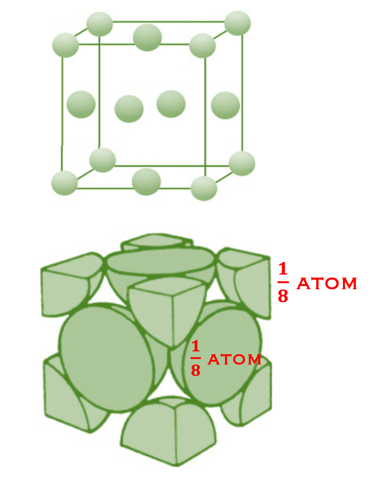
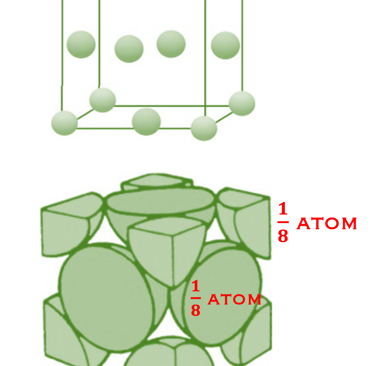
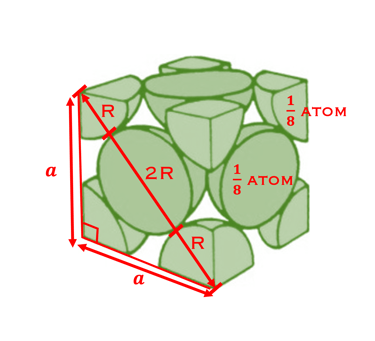
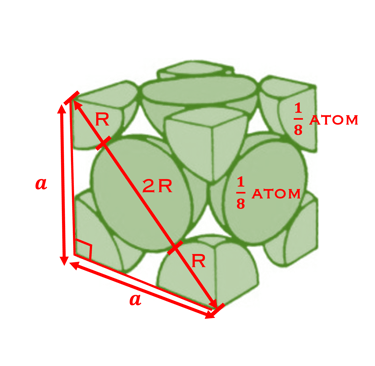
HINT: Nous considérons l'une des faces cubiques illustrée ci-dessous
La diagonale, D est fonction de a par la relation:
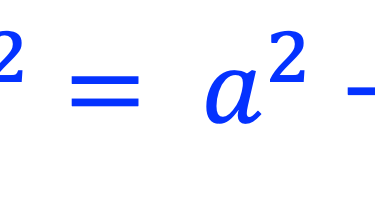
La diagonale relie les deux coins (contenant deux atome chacun) et contient un atome au centre du diamètre 2R

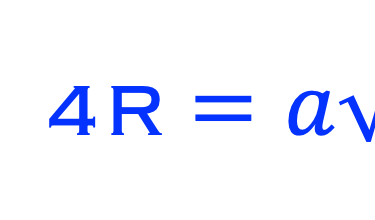
APF est une mesure du volume total de la sphère atomique dans une cellule unitaire

Concentration atomique


Comme une mole de matière pèse 𝑀𝐴𝑇𝑂𝑀 grammes et contient 𝑁a (Avogadro) atomes, la densité 𝜌
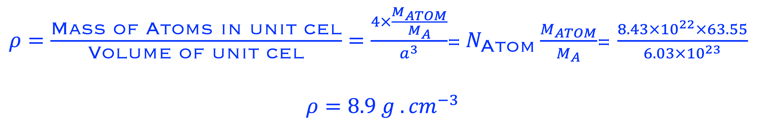
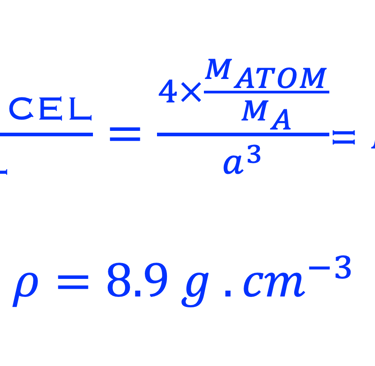
HINT: (exercice à droite): Le plan est parallèle à l'axe z, donc l'ordonnée à l'origine est ∞. Les ordonnées de le plan sont 𝐚/2, 𝐛, et ∞ le long des axes x, y,
z respectivement, donc les ordonnées en termes de 𝐚, 𝐛, 𝐜 sont ½, 1, ∞, et les réciproques des intercepts de sont:
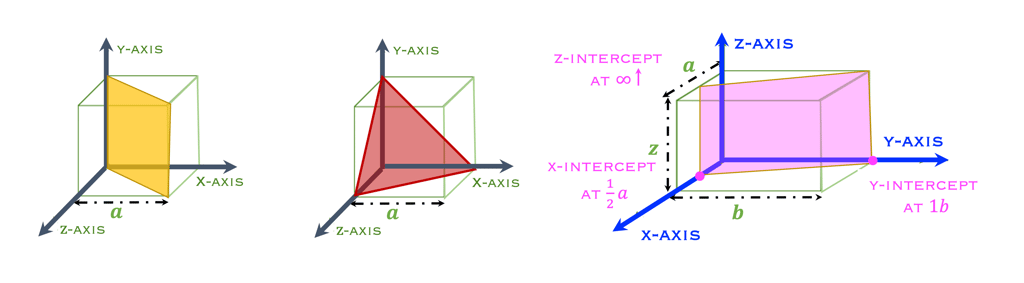
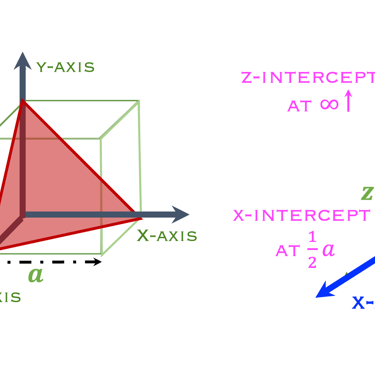
QUIZ: Trouver les indices de Miller des plans colorés
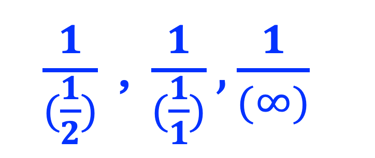
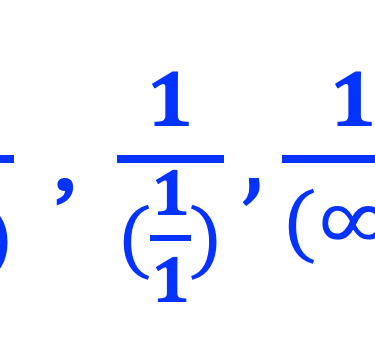
Les indices de Miller: <hkl> = 2,1,0
Faire les deux autres exercices
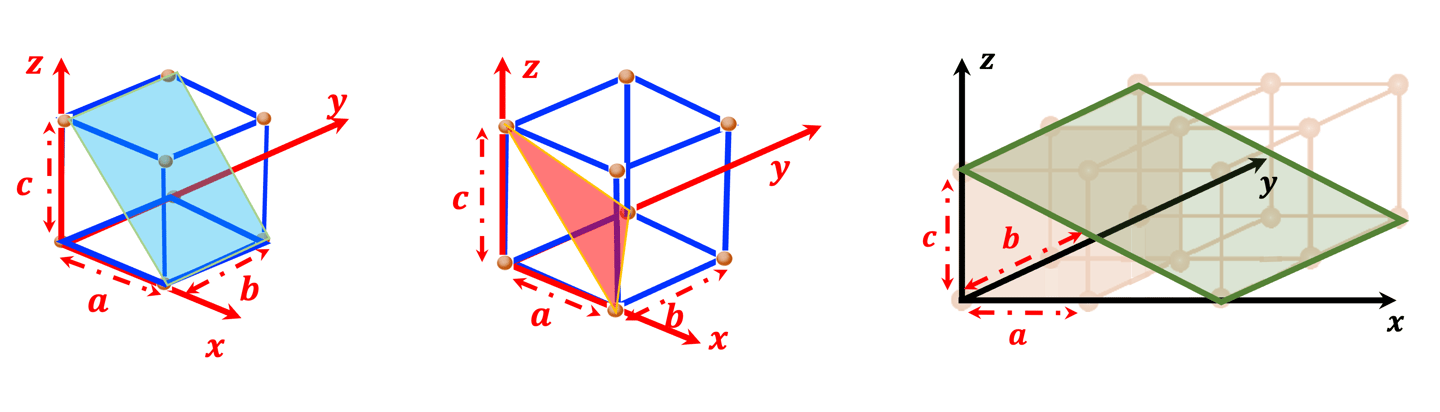
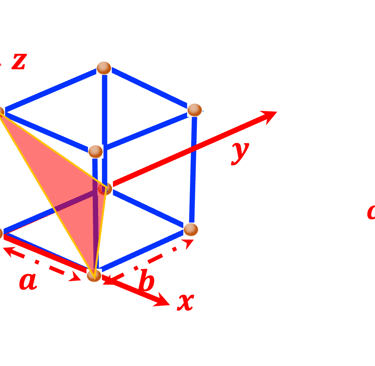
QUIZ: Identifier les trois plan (111) , (102), (101) et trouvez les indices de Miller dans le réseau cristallin de chacun d´eux
La diffractométrie des rayons X
La diffractométrie des rayons X est l'une des techniques non destructives les plus utilisée pour caractériser les matériaux cristallins.
Un diagramme de diffraction des rayons X, permet d'identifier la structure cristalline, les phases, la taille moyenne des grains, trouver les indices de Miller et les paramètres du réseau.
Le diagramme de diffraction des rayons X en 2θ délivre tous les pics et les valeurs « hkl » correspondants
Les rayons X sont produits en bombardant une cible métallique (comme le Cu ou le Mo) avec un faisceau d'électrons émis par un filament chaud (e.g. le tungstène, W)
Les électrons de la coquille K (1s) de l'atome cible sont ionisés et des rayons X sont émis lorsque les lacunes qui en résultent sont comblées par des électrons descendant des niveaux L (2P) ou M (3p). Cela donne lieu à des lignes α « K » (Cu “Kα = 1,5418 Å ; Mo Kα = 0,7107 Å )
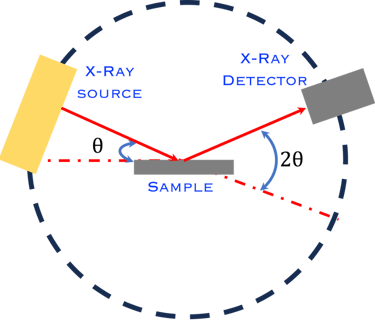
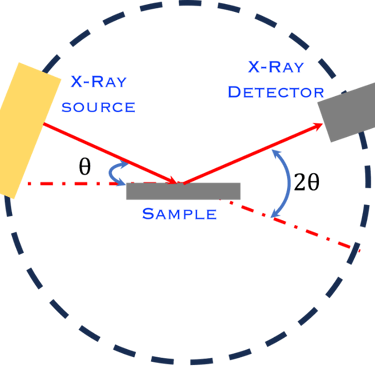
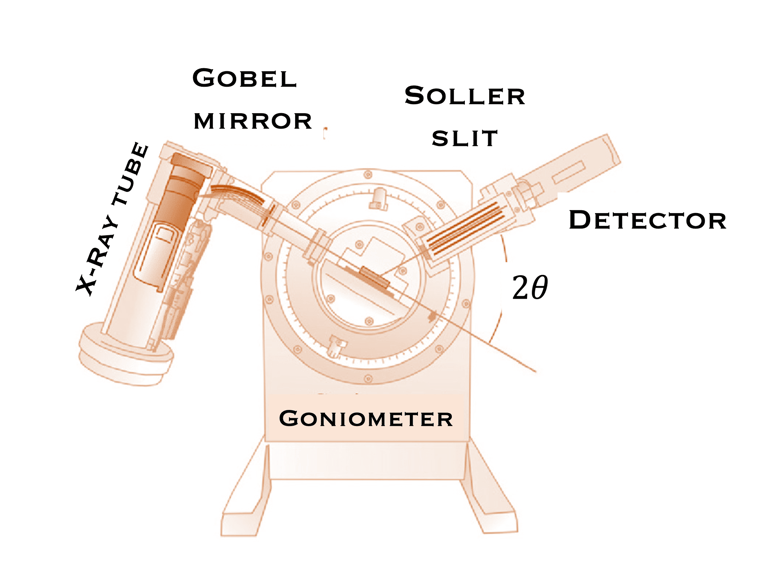
La quantité de mouvement d'une particule est liée à une onde par la relation de Broglie: λ=h/p où p est la quantité de mouvement, λ est la longueur d'onde de Broglie et h la constante de Planck
Nous avons besoin d'une longueur d'onde « de Broglie » de l'ordre de l'espacement inter-atomique (de l'ordre de l'Angström)
Un grand nombre de plans parallèles séparés par la même distance, 𝑑hk𝑙 , produit des pics de diffraction importants lorsque l'angle entre le faisceau incident et la surface de l'échantillon satisfait à la condition de Bragg.
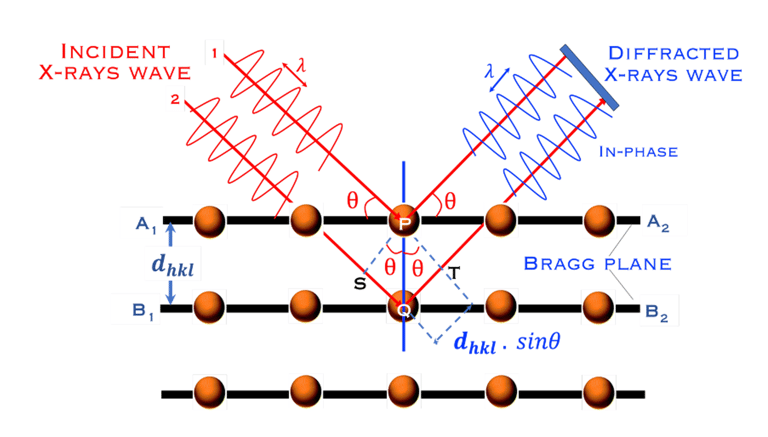
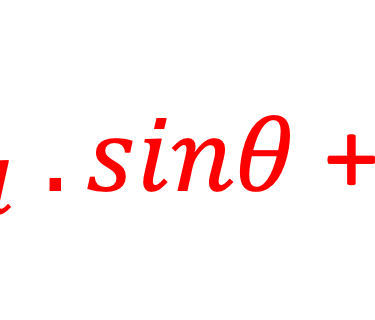
La différence de parcours entre deux ondes X incidentes (1) et (2) de longueur d'onde λ qui se réfléchissent sur deux plans successifs (diffusées par les atomes aux ponts P et Q) est donnée par la relation de Bragg
Les interférences constructives des ondes X diffractées sont analysées selon la loi de Bragg ou condition n . λ = 2dhkl . sinθ
L'ordre de réflexion 𝑛 est un nombre entier (1, 2, 3...) et 𝑠𝑖𝑛𝜃 n'excédant pas 1
On obtient des interférences constructives ou destructives
La distance entre les plans adjacents de l'ensemble (hkl) d'un matériau à structure cubique, et le paramètre de réseau (a) peuvent être obtenus à partir de l'équation
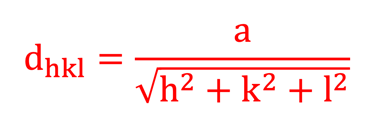
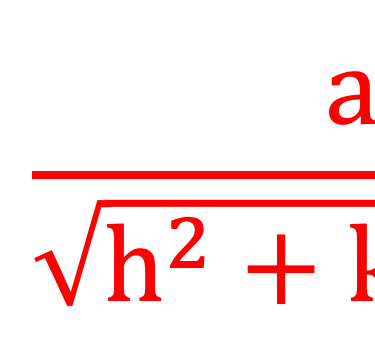
En utilisant la loi de Bragg, l'équation ci-dessus devient
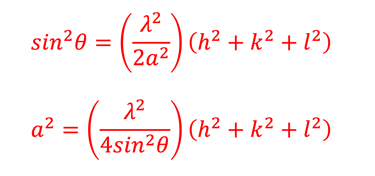
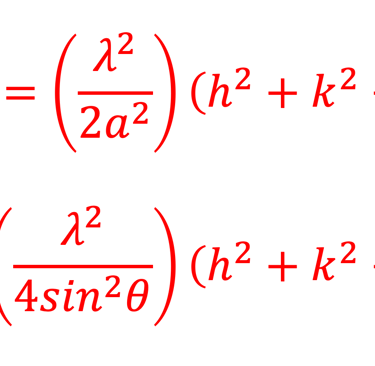
On peut indexer la figure de diffraction et trouver le réseau de Bravais et les paramètres de réseau de n'importe quelle structure cristalline cubique.
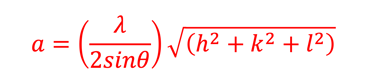
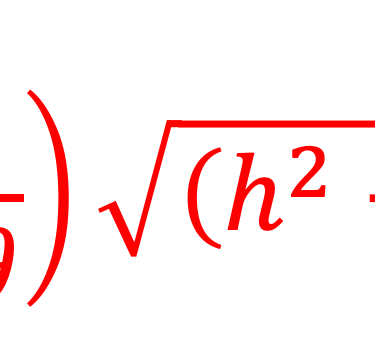
Je renvoie le lecteur de voir nos travaux sur l'utilisation de XRD pour explorer les matériaux binaires, ternaires et quaternaires pour la conversion photovoltaïque de l'énergie solaire (PhD thesis by Xianzhong Lin
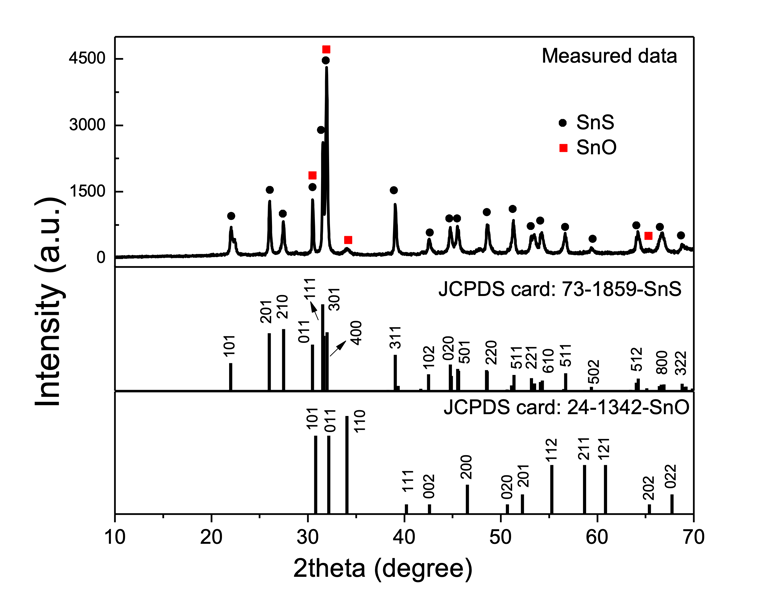
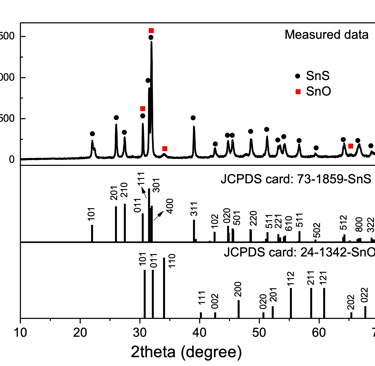
Le diagramme XRD des nanoparticules (échanitillon SnS-250) montre clairement que presque tous les pics de diffraction peuvent être attribués à la structure orthorhombique SnS à l'exception du pic situé à environ 2θ = 34°.
Ce pic à 2θ = 34° correspond à la réflexion (101) de la structure orthorhombique SnO (JCPDS 24-1342).
Le calcule des paramètres de réseau à partir du diagramme XRD en choisissant trois des plans de réseau à l'aide de l'équation
Les valeurs obtenues de a = 11,192 Å, b = 3,985 Å et c = 4,323 Å sont en bon accord avec la carte standard JPCDS 73-1859 pour la structure orthorhombique SnS où a = 11,18 Å, b = 3,982 Å et c = 4,329 Å.
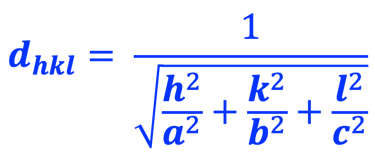
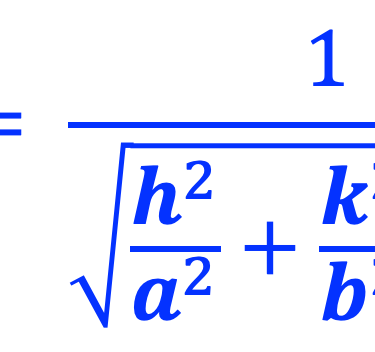
Plus information: se référer au PhD de Xianzhong Lin TU-Berlin (à télécharger ici)
Microscopie électronique à transmission
On peut former des images de haute résolution à l'aide d'un microscope électronique à transmission en utilisant un faisceau d'électrons et des champs magnétiques pour focaliser les électrons (lentilles électroniques à bobine magnétique)
Les lentilles électromagnétiques focalisent et grossissent le faisceau d'électrons après qu'il a été transmis à travers un échantillon ultra mince assurant une bonne résolution
L´ image finale avec un grossissement allant jusqu'à plusieurs 100 000x est projetée sur écran d'imagerie
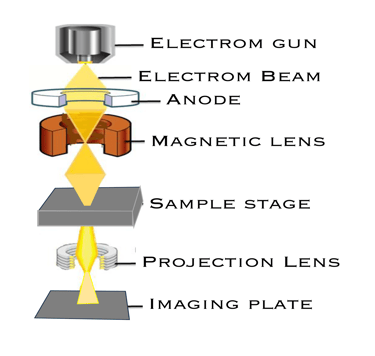
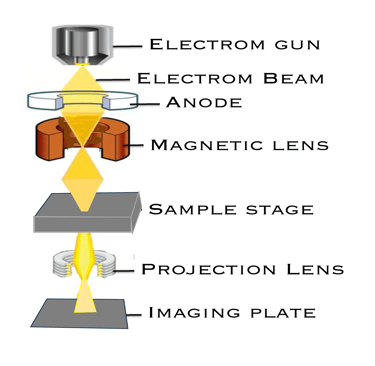
The illustration shows a source sending a beam of electrons condensed by the lenses into a beam to the sample, the electrons passing through the sample are focused by a series of projected lens to from a real, enlarged image of the sample
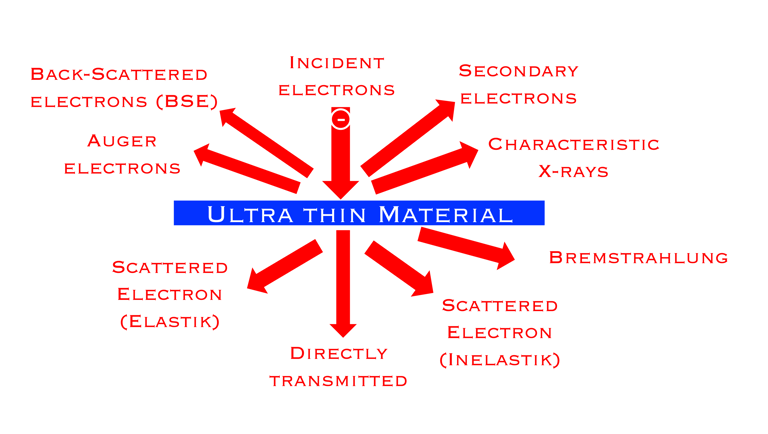
Comme c'est illustré sur la figure ici, la microscopie électronique à transmission est un outil pluridisciplinaire qui inclue la diffraction dans l'espace réciproque, l'imagerie dans l'espace réel et la spectroscopie, permettant une caractérisation complète et une haute résolution dans le temps, l'espace, voire la quantité de mouvement et, même de l'énergie.
Je renvoie le lecteur de voir nos travaux sur l'utilisation de TEM pour explorer les matériaux binaires, ternaires et quaternaires pour la conversion photovoltaïque de l'énergie solaire (PhD thesis by Xianzhong Lin
11.3% efficiency Cu (In, Ga)(S, Se) 2 thin film solar cells via drop-on-demand inkjet printing, X. Lin, R. Klenk, L. Wang, T. Köhler, J. Albert, S. Fiechter, A. Ennaoui, Energy & Environmental Science 9 (6) (2016) 2037
The crystallisation of Cu2ZnSnS4 thin film solar cell absorbers from co-electroplated Cu–Zn–Sn precursors, Roland Schurr, A Hölzing, Stefan Jost, Rainer Hock, Torsten Voβ, Jörg Schulze, A Kirbs, Ahmed Ennaoui, M Lux-Steiner, Alfons Weber, I Kötschau, H-W Schock. Thin Solid Films 517, 7, (2009) pp. 2465
Structural and optical properties of Cu2ZnSnS4 thin film absorbers from ZnS and Cu3SnS4 nanoparticle precursors, Xianzhong Lin, Jaison Kavalakkatt, Kai Kornhuber, Sergiu Levcenko, Martha Ch Lux-Steiner, Ahmed Ennaoui. Thin Solid Films 535 (2013) 10
Inkjet‐Printed Cu2ZnSn(S, Se)4 Solar Cells, Xianzhong Lin, Jaison Kavalakkatt, Martha Ch Lux‐Steiner, Ahmed Ennaoui. Adv. Sci. 2015, 2, 1500028 (1-6)
One-step solution-based synthesis and characterization of kuramite Cu3SnS4 nanocrystals, Xianzhong Lin, Alexander Steigert, Martha Ch. Lux-Steiner and Ahmed Ennaoui. RSC Advances, 2012, 2, 9798
Highly Textured Films of Layered Metal Disulfide 2H‐WS2: Preparation and Optoelectronic Properties Autoren A Matthäus, A Ennaoui, S Fiechter, S Tiefenbacher, T Kiesewetter, K Diesner, I Sieber, W Jaegermann, T Tsirlina, Reshef Tenne. J. Electrochem. Soc. 144 (1997) 1013
Synthesis of Cu2ZnxSnySe1+x+2y nanocrystals with wurtzite-derived structure, Xianzhong Lin, Jaison Kavalakkatt, Kai Kornhuber, Daniel Abou-Ras, Susan Schorr, Martha Ch. Lux-Steiner and Ahmed Ennaoui. RSC Advances, 2012, 2, 9894
Cu2ZnSn(S, Se)4 thin film absorbers based on ZnS, SnS and Cu3SnS4 nanoparticle inks: Enhanced solar cells performance by using a two-step annealing process, Xianzhong Lin, Jaison Kavalakkatt, Ahmed Ennaoui, Martha Ch. Lux-Steiner. Solar Energy Materials and Solar Cells 132, (2015), 221
Illustration (left) from PhD thesis by Xianzhong Lin on TEM and HRTEM images of samples from the contrast experiments: (a) and (b): SnS-200; (c) and (d) SnS-300; (e) and (f) SnS-300-2. // https://api-depositonce.tu-berlin.de/server/api/core/bitstreams/3b7d5844-9ffe-43b8-8a2c-7c33253bc2b4/content


Avant de continuer regarder cette video de Mark Lundstrom at Purdue University.


I.2 - Dualité ondes-particule
Il y a des expériences où une particule (e.g. l'électron), se comporte comme une particule caractérisée par son énergie et d'autres expériences où la particule se comporte comme une onde caractérisée par sa longue d'onde.
On peut faire des diffractions avec les rayon X par exemple
On peut également obtenir des interférences des électrons
On peut arracher un électron de la matière par irradiation (e.g. effet photoélectrique)
L'hypothèse de Albert Einstein (en 1905), suppose que les atomes absorbent et émettent de l’énergie lumineuse par quanta, d´énergie i.e. les ondes lumineuses transportent leur énergie sous forme de corpuscules de lumière E = hν
En réalité, Albert Einstein avait rejoint la théorie de Max Planck, sur les quanta (1900), qui désigna par h (constante de Planck) qui décrit la taille des quanta

On définit également la grandeur associée appelée "quantum d'action", ou "constante de Planck réduite"
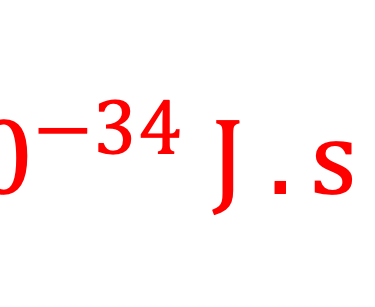
L'énergie, E d'une particule est reliée à sa fréquence par : E = hν
Louis de Broglie (en 1924), avait proposé le caractère corpusculaire et ondulatoire de toute particule matérielle. Louis de Broglie avait donné la relation devenue célèbre entre la longueur d'onde (λ) d'une particule et sa quantité de mouvement (p = mv): soit l'équation p = h/λ, qui s'annonce comme suit: une particule de masse m de vitesse v, possède une longueur d'onde λ donnée par: λ = h/p = h/(mv).
Les propriétés ondulatoires peuvent l’emportent sur les propriétés corpusculaires, ceci fait apparaitre le concept de délocalisation et d´indiscernabilité, qui jouent un rôle important en physique atomique et en physique des solides, la particule perd sa localisation, une propriété plutôt corpusculaire.
Une autre propriété des particules joue un rôle fondamental, le spin. dont les valeurs sont des multiples entiers ou demi-entiers de la constante réduite de Planck. (e.g. les valeurs du spin de l’électron sont (+h/2 , - h/2). La valeur du spin du photon un spin est 1.
Les quanta de spin demi-entier ne peuvent jamais coexister dans des états physiques individuels identiques, on les nomme fermions.
Les quanta de spin entier, eux, peuvent s’accumuler dans des états identiques, on les nomme bosons. Les photons sont des bosons, par contre les électrons sont des Fermions. Regarder la video

Dimensions atomique et incertitude
Nous avons bien souligné dans l'introduction intitulée "De la physique de newton à la physique statistique quantique et la physique des cellules solaires" qu'en physique classique, l'évolution d'une particule est décrite par la donnée de sa trajectoire dans l'espace de phase: un espace à six dimensions {q ⃗(t) ; p ⃗(t)} qui sont les coordonnées et les impulsions généralisées de la particule. En physique quantique la notion de trajectoire n'existe plus et on parlera de la probabilité de présence d'une particule. Le principe d'incertitude de Werner Heisenberg (1927) limite la précision de mesure quand on cherche à déterminer par exemple position et vitesse d'une particule atomique ou subatomique. Nous formulons ce principe comme suit: Le produit Δx l'incertitude sur la position d'une particule par Δp l'incertitude sur sa quantité de mouvement est supérieur ou égal à la moitié de la constante de Planck réduite, mathématiquement parlant:
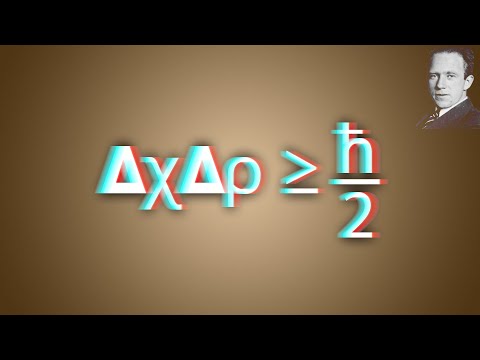
Alain Aspect Prix Nobel de physique 2022 explique l’intrication quantique, je cite [Ref. 1] "c'est un phénomène quantique dans lequel deux particules au moins partagent les mêmes propriétés. Quand on mesure l'état de l'une d'entre elles, les autres particules intriquées prennent instantanément la même valeur, indépendamment de la distance entre elles" fin de citation. Wikipedia [Ref.2] décrit intrication quantique comme étant, je cite wikipedia "'intrication quantique, ou enchevêtrement quantique, est un phénomène dans lequel deux particules (ou groupes de particules) forment un système lié et présentent des états quantiques dépendant l'un de l'autre quelle que soit la distance qui les sépare" fin de citation. La technologie utilisera l'intrication quantique dans les domaines de de l'ordinateur quantique, la cryptographie quantique, et la téléporttion quantique. Regarder la vidéo

Je vous invite à regarder les videos, avant de continuer
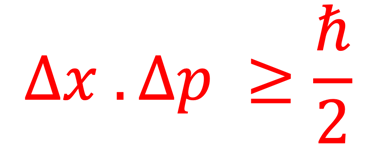
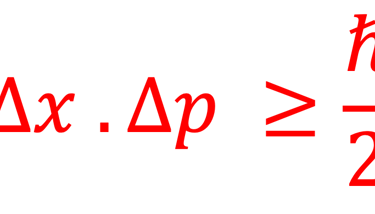

Quiz 1: A beam of light strikes a metal surface having a work function Φ = 4.3 eV, thus electrons with a kinetic energy of 7.9 eV are ejected. What is the energy of incident light?
Can we extract electron with photon energy as follow:
E > Φ
E < Φ
3 photons with energy E = Φ/2 For each photon
Watch the video from MIT Fall 2014 and Explain the photoelectric effect
Quiz 2: Light of 100 μW is incident on a photodetector. (a) If the light is green (500 nm), how many photons are striking the surface per second?


Quantum mechnics and quantum numbers
Nous avons discuté plu haut la différence essentielle et radicale entre la mécanique classique et la mécanique quantique. La première celle de Newton décrit une particule par un point de l'espacé des phases {q ⃗(t) ; p ⃗(t)}, alors que en mécanique quantique, une particule atomique et subatomique est plutôt un objet étendu, décrit par une fonction d'onde ψ(n,l,m) qui gouvernent l'évolution de la particule selon une équation: celle de Schrödinger que nous écrivons ici à une dimension ou pour des problèmes à un degré de liberté (i.e. l'espace des phases est (x,p) de dimension 2.
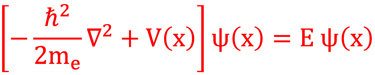
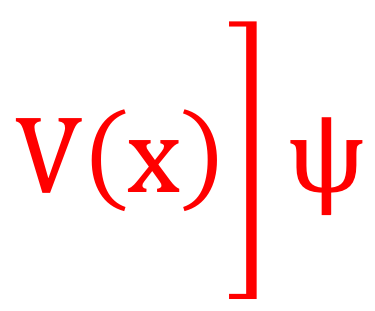
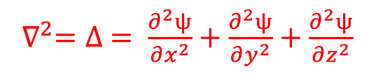
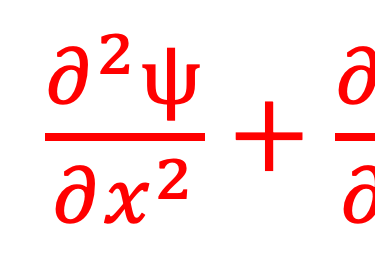
L'équation de Schrödinger permet de déterminer la probabilité qu'un électron se trouvant dans l'espace pour ψ(r ) ou le long d'un seul axe (l'axe des x) pour ψ(x)
La notion de trajectoire perd son sens et est remplacée par une probabilité de présence de l'électron dans un volume d'espace autour du noyau
La résolution de l'équation d'onde pour un système (e.g. atome d'H2) permet d'obtenir les fonctions d'onde, ou orbitales, et leurs énergies correspondantes
Chaque orbitale décrit une distribution spatiale de la densité électronique
Quiz: Nous allons voir qu'une orbitale est décrite par un ensemble de 3 nombres quantiques introduits naturellement (n,l,m). La fonction d'onde est ψ = ψ(n,l,m)
à trois dimension ψ = ψ(r = x,y,z) est la fonction d'onde et le Laplacien Δ est:
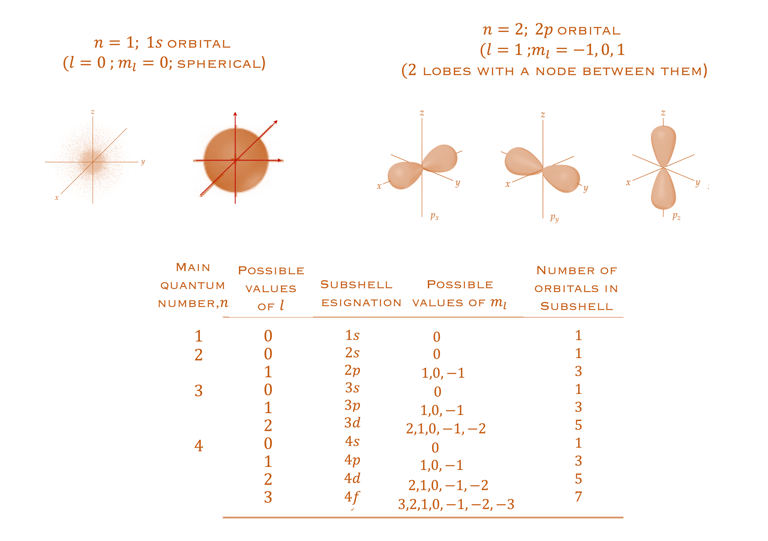
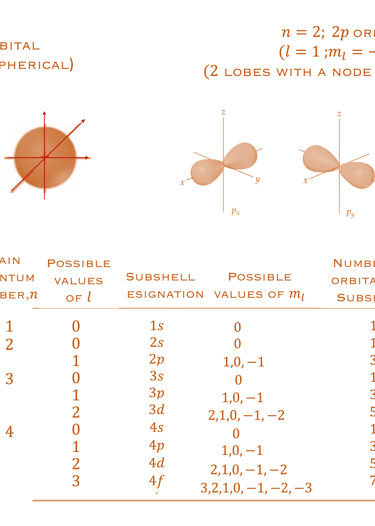
répartition spatiale constitue le nuage électronique autour du noyau, ou ensemble des points de l’espace (r, θ, φ) ayant une probabilité non nulle d’être occupés par l’électron ( un problème sera consacré à cette parti du cours
Regarder la video et envoyer vos questions à travers:
Ahmed Ennaoui
dr.ahmed.ennaoui@ieee.org
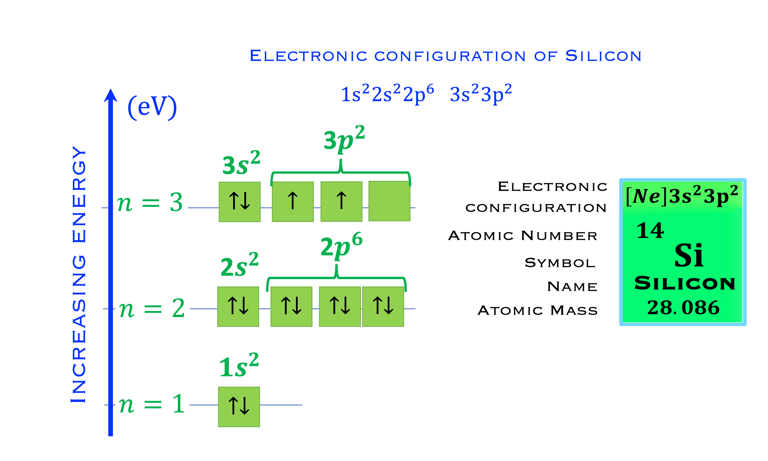
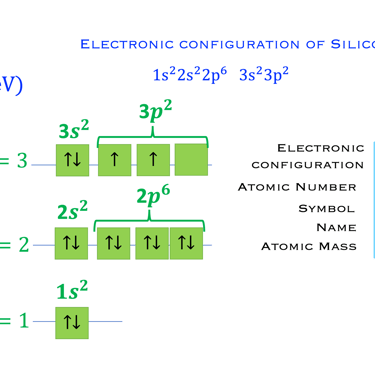
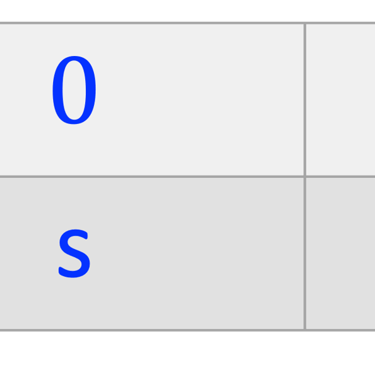
Le diagramme des orbitales est représenté sur la figure ci-dessous pour le Silicium
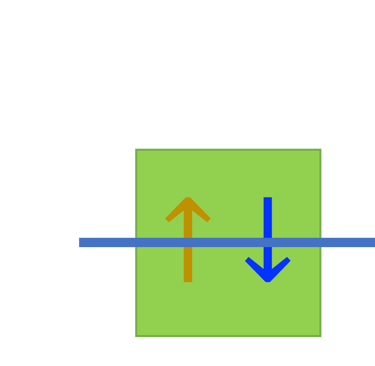
Chaque case correspond à une orbitale
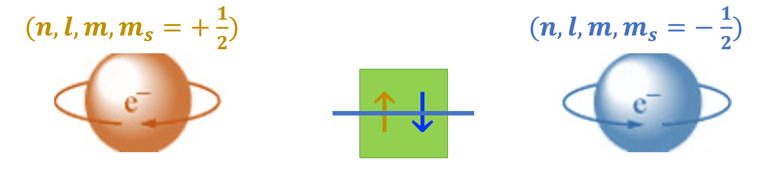
Les flèches représentent l'électron
La direction de la flèche représente le spin de l'électron
Selon le principe de Pauli, deux électrons d'un même atome ne peuvent être décrits par le même ensemble de nombres quantiques (n, l, m, ms) qui sont:
𝑛: nombre quantique principal décrivant le niveau d'énergie de l'orbitale 𝑛 ≥ 0
𝑙, est le nombre quantique azimutal décrivant la forme de l'orbital, allant de 0 à (𝑛-1)
Les orientations tridimensionnelles de l'orbitale sont décrites par des nombres quantiques magnétiques, -𝑙 ≤ 𝑚𝑙 ≤ +𝑙

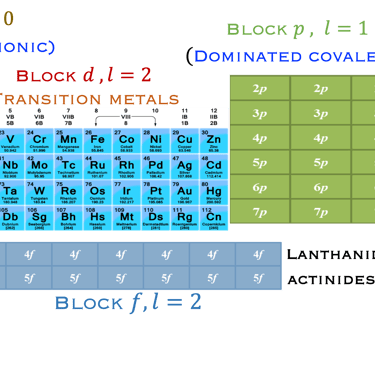
Le lien avec le tableau périodique
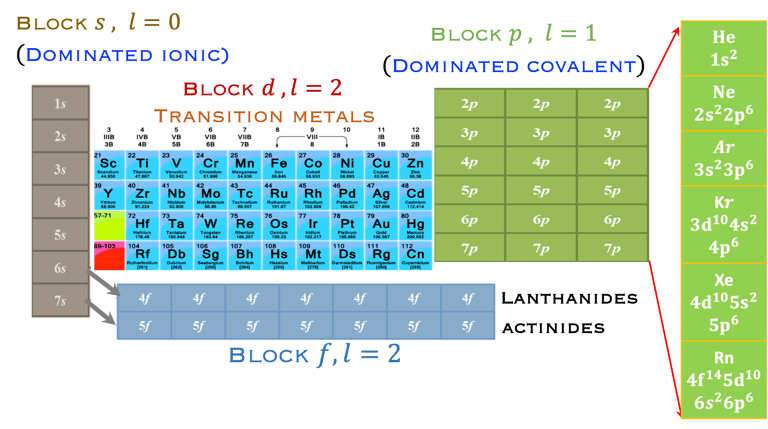
Il est important de connaitre l'arrangement des électrons dans l'atome afin prédire les liaisons orbitales et chimiques. Le tableau ci-dessous permet d´idenfier
7 rows (horizontal) → periods
18 vertical columns → groups
Alkali metals → Group 1
alkaline earth metals → Group 2
halogens → Group 17
noble gases → Group 18
Transition metals
Regarder la video et essayer de retrouver chaque élément du tableau périodique
Envoyer vos questions à travers: Prof. Ahmed Ennaoui dr.ahmed.ennaoui@ieee.org

Liaisons chimiques et niveaux d'énergie
Les atomes se combinent et sont maintenus ensemble par de fortes forces d'attraction appelées « liaisons chimiques »
Les liaisons chimiques résultent de l'interaction entre les électrons de valence des atomes qui se combinent
D'une manière générale on peut distinguer plusieurs sorte de liaisons chimiques:
Liaisons ioniques, où les éléments des groupes I et II (électro-négativité la plus faible) cèdent leurs électrons
Les éléments du groupe VII (électronégativité la plus élevée) gagnent les électrons et obtiennent la configuration de gaz noble
Liaisons covalentes où deux atomes ou plus partagent une ou plusieurs paires d'électrons formant un réseau
Chaque paire est considérée comme une liaison unique liée avec les atomes adjacents
Liaison covalente polaire avec des électronégativités différentes
Liaison covalente non polaire avec les mêmes électronégativités
Les liaisons de Van der Waals nettement plus faibles comparées aux liaisons covalentes ou ioniques
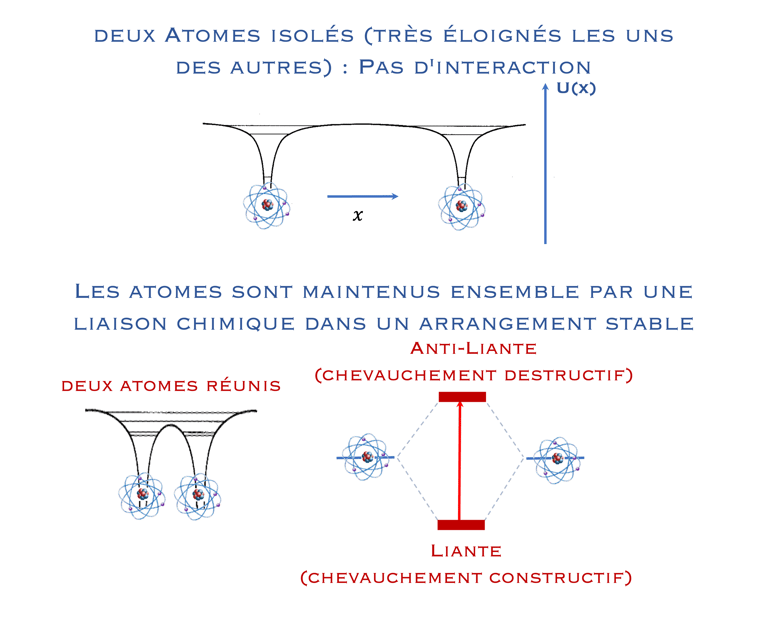
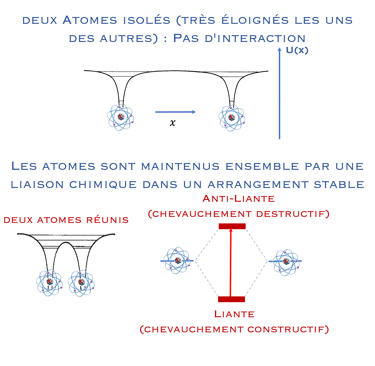
From "Single Energy Levels” to “Bands Energy Levels”
Jusqu`a présent il était question de niveaux d'énergie d'un comportement d’un atome isolé où les électrons occupent certaines orbites autour du noyau atomique dont les énergies discrètes sont dictées par la mécanique quantique (principe d'exclusion de Pauli). les électrons peuvent changer d'orbite en absorbant ou en émettant un photon dont l’énergie sera exactement la différence d’énergie entre les deux orbites
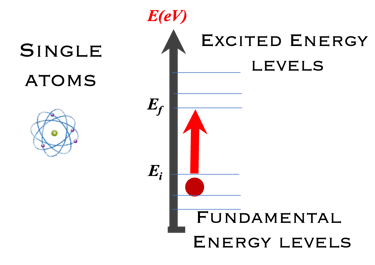
Comment change la situation si on prend un grand nombre d’atomes formant un solide ?
Les échanges entre les états d'énergies différentes dépendent lorsque les atomes sont assez rapprochés pour devoir prendre une structure solide sont complètement différentes. les orbites des atomes individuels tendent à former des bandes énergétiques qui reste encore de nature discrète néanmoins, elles prennent une game de valeur d´énergies très rapprochés appelé bandes bandes d´énergie
La bande supérieur sur la figure à droite est une bande d’énergie vide ou partiellement occupée et dont les électrons peuvent être extraits par l’action d’un champ électrique externe, cette bande est appelée la bande de conduction
La bande où les électrons sont plus attachés à leur atome est la bande de valence, composé d’orbitales dont les électrons, dits de valence, peuvent passer à la bande de conduction par absorption de photons
Entre les bandes d´énergie se trouve la bande interdite où les électrons ne peuvent se retrouver dans les orbites ayant cette énergie , ceci est imposé par la mécanique quantique
Finalement je veut mettre le point sur l'assemblage d'un nombre fini de particules (led nanoparticules et les nano-clusters) qui représentent un état de la matière situé entre les solides en vrac et les structures moléculaires, leurs propriétés physiques et chimiques passent progressivement de l'état moléculaire à l'état solide, avec l'augmentation de la taille des particules.
Ainsi, le nombre d'atomes de surface des nanoparticles de diamètre de quelques nanomètres, est comparable à celui des atomes situés dans le volume cristallin. Ceci se traduisent par des propriétés de transport entièrement différentes comparées au les solides massif
La taille des nano-particules particules influe le largeur HOMO-LUMO de la bande interdite du matériaux (voir figure du milieu)
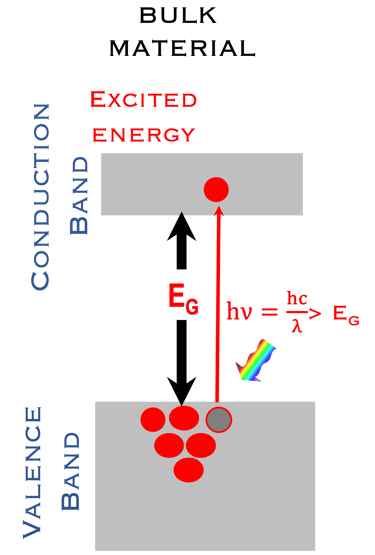
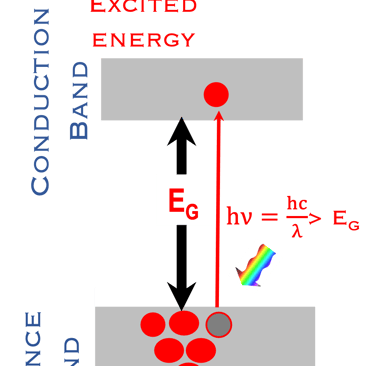
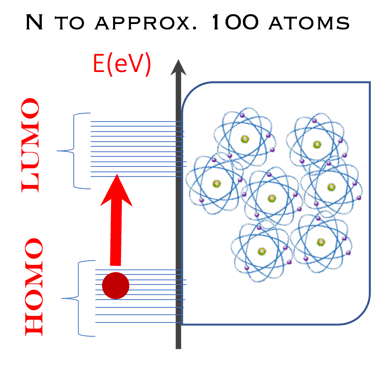
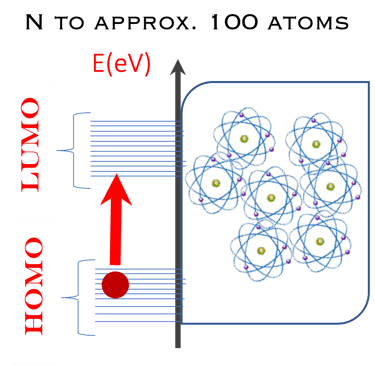
La mécanique quantique décrit un électron par une fonction d'onde. Lorsque les électrons de deux atomes, par exemple l'atome d´Hydrogène, se rapprochent, leurs fonctions d'onde électroniques se chevauchent, ce qui signifie mathématiquement que la fonction d'onde devient une combinaison linéaire des deux fonctions d'onde individuelles (addition et soustraction), ceci entraîne la formation d'une orbitale moléculaire de liaison liante (état symétrique donné par l'addition de deux fonctions d'onde) et d'une orbitale moléculaire anti-liante (état antisymétrique donné par la soustraction de deux fonctions d'onde).
Le rayonnement du corps noir
Nous considérons l´impulsion p ⃗(px, py, pz) = ℏK ⃗ où px, py, pz représente les composantes de p ⃗ dans un système de coordonnées. K ⃗est le vecteur d´ondede coordonnées (kx, ky, kz ) et ℏ=h/2π (h est constante de Planck)
Nous considérons un élément de volume élémentaire dans ce système de coordonnée (espace des K ⃗ ), représenté par un cube de cotés Lx , Ly, et Lz de sorte que Lx x Ly xt Lz = Volume V de l'espace K occupé par 1 point comme indiqué sur la figure ci-dessous
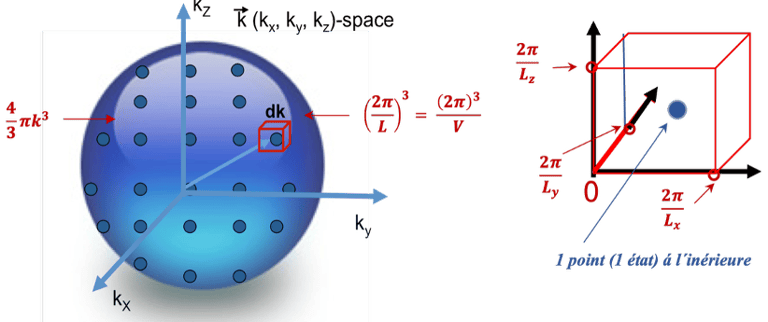
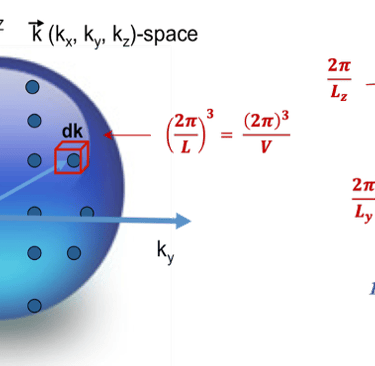
Il s´agit de photons, ce sont des Bosons, alors le nombre d´occupation ou "probabilité » d'occupation <Np(ε,T)> d'un état individuel d'énergie ε est donné par la statistique de Bose-Einstein définit par la relation*:


Le nombre d'états (# de points) dans l´espace des K ⃗ est:
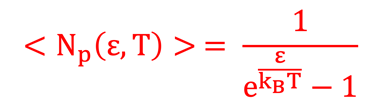
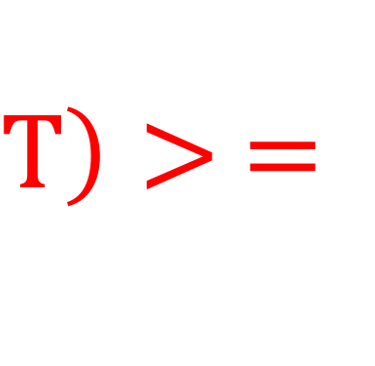


(*) Pour mieux comprendre l’emploi de la distribution de Bose-Einstein et le formalisme grand-canonique, je renvoie le lecteur au cours de maitrise de physique (voir le livre de Diu cité ici comme référence), bien entendu ce formalisme n´est pas nécessaire pour continuer ce cours
**La relation énergie-impulsion d’une particule relativiste est donnée par la relation
L´indice p dans la probabilité <Np (ε,T)> indique qu'il s'agit de l´impulsion du photon que nous rappelons relié à l´énergie ε du photon** par: ε = p . c
kB= est la constante de Boltzmann
Nous cherchons la loi de Planck qui permettra de donner la densité des états spectrale en Energie. Notons ρ(K) ou ρ(ω) la densité des états
Reprenons la relation du nombre d'états dans l´espace des K ⃗ que nous formulons dans un intervalle [ω , ω+∆ω] ou ce qui revient au même dans l'intervalle ∆K c'est à dire [K , K+∆K] ou en terme d´énergie [ε ,ε+∆ε]
Pour les photons on doit corriger le nombre d'état en considérant deux états" de polarisation et multiplier par 2 la densité d´état:
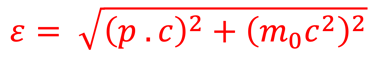
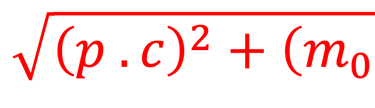
ε est l'énergie, p la quantité de mouvement, et est m0 la masse au repos. qui dans le cas du photons m0 = 0 ( car un photon au repos n'existe pas), alors cette relation se simplifie en une dispersion linéaire ε = p . c
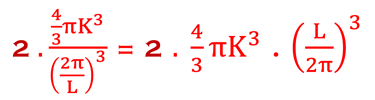
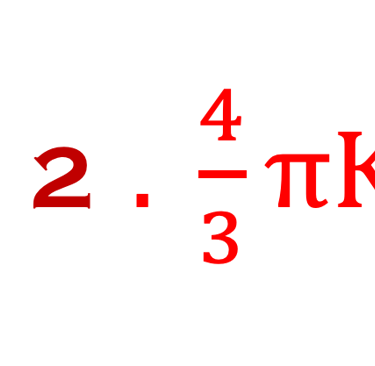
Nous partons de cette relation pour trouver le nombre d'état ∆N dans l´intervalle [K , K+∆K]:

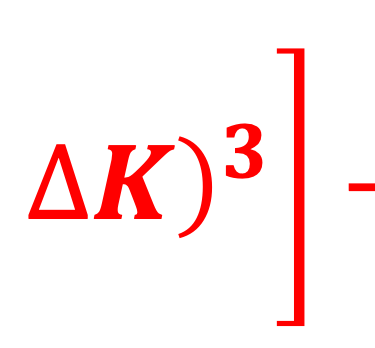
∆K<<1 (infinitésimal) ∆Np(K,T) → dNp(K,T)
On peut utiliser les propriété d´une "fonction continue f(x) et sa differencielle df(x) = f´(x)dx où f´(x) c'est la limite lorsque (∆x→0) du taux d'accroissement [f(x+∆x)-f(x)]/∆x qui est la définition de la dérivé
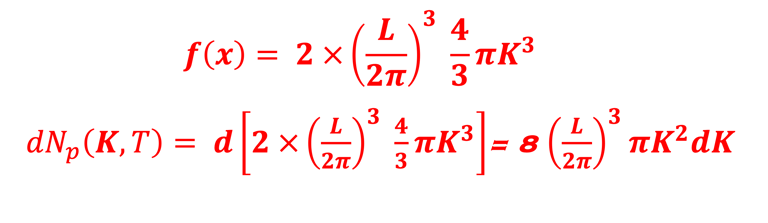
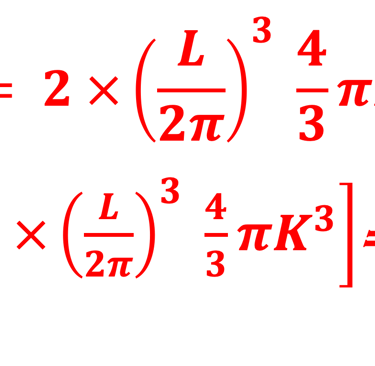
On peut faire apparaitre la fréquence angulaire ω des photons K= ω/c où c est la vitesse de la lumière dans le vide
Les équations de Maxwell appliquées à une onde électromagnétique impose au vecteur d´onde K ⃗ du "PHOTON" d´être lié à sa pulsation ω par:
|K ⃗ |=K= ω/c
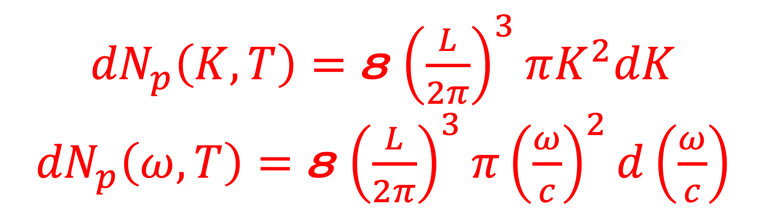
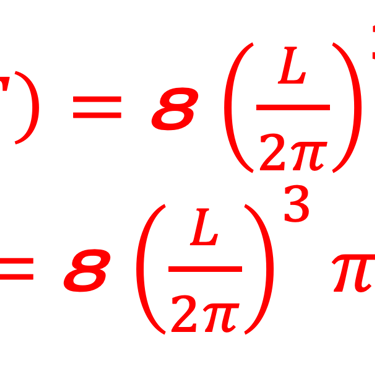
L'expression de de la densité d´état en fréquence ω se déduit tout simplement (nous avons introduit le volume élémentaire V = L x L x L)

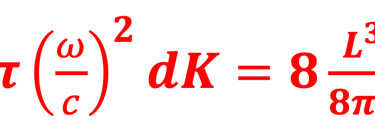
Les photons sont des Bosons on doit donc moduler ρ(ε, V) par la probabilité d´occupation <Np (ε,T)> de Bose-Eistein


La densité d'état peut aussi s'exprimer en fonction de l'énergie des photons ε = ℏω
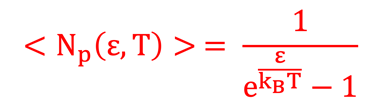
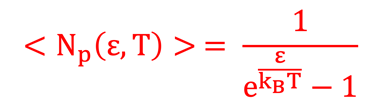
L´occupation des photons ayant leurs énergiescomprise entre ε et ε + dε est:
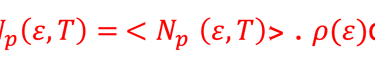
L´énergie d´occupation dans l´ interval [ε, ε + dε] s´obtient en multipliant le nombre d’occupation par l´énergie de chaque "PHOTON" occupant cet état:
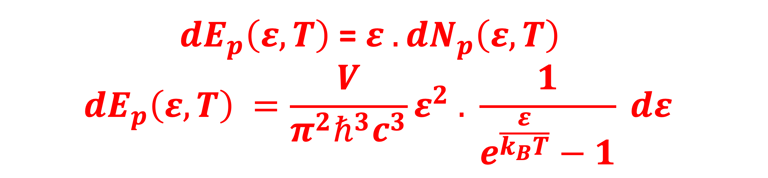
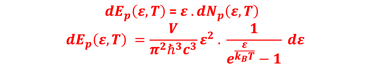


Notons u(ω,T) dω la densité d´énergie par unité de volume dans la bande de fréquence [ω , ω+dω]
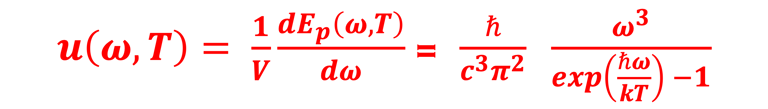
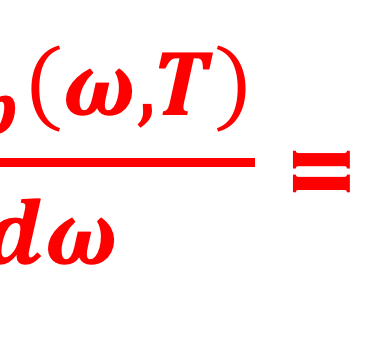
Dans cette expression de u(ω,T), ω = 2πν est la fréquence angulaire, ν = c/λ relie la fréquence à la longueur d´onde λ et ε = ℏω relie la fréquence angulaire ω
à l´énergie ε du photon énergie, C´est la loi de Planck pour le rayonnement
du "CORPS NOIR"
QUIZ (exercice): Changement de variable x= ℏω/kT
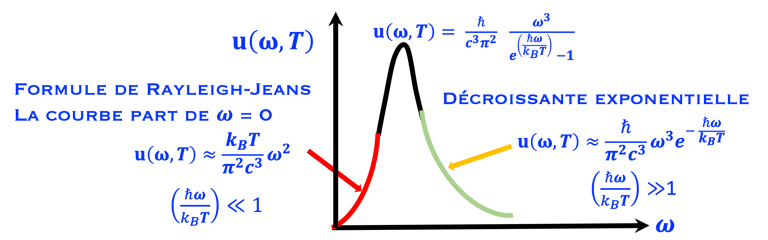
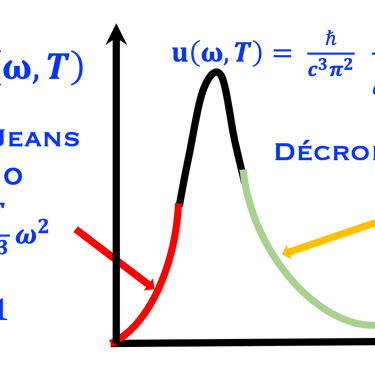
(1) Trouver la formule de Rayleigh-Jean pour les faible fréquence ℏω/kT≪1 ou ℏω≪kT (croissance parabolique en fonction de ω)
(2) Trouver le résultat pour les hautes fréquences ℏω/kT ≫1. ou ℏω≫kT (décroissance exponentielle)
(3) Tracer u(ω,T) en fonction de ω, comme suit et expliquer chaque partie de la courbe
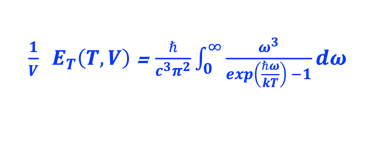
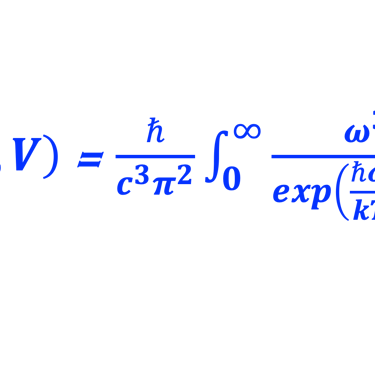
(1) Poser x = ℏω/kT et montrer l'intégrale:
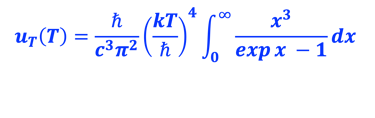
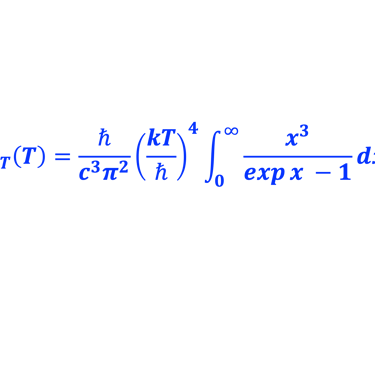
(2) Monter que l´énergie totale rayonnée est donnée par*:
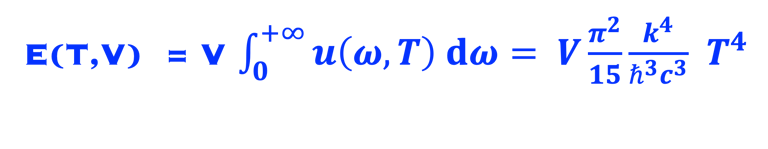
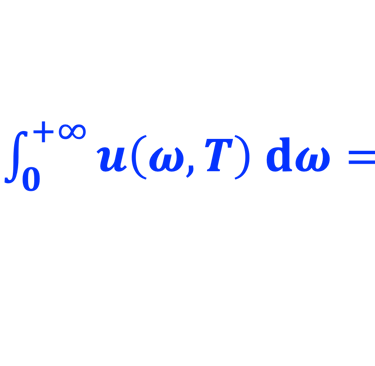
(2) faire l´application numérique et retrouver la loi de Stefan suivante (les données pour l'application numérique vous les trouvez dans la video ci-dessous:


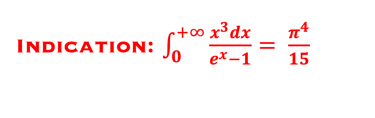
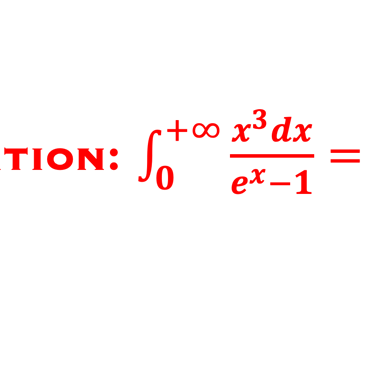
(4) Retrouver la loi de Planck pour le rayonnement du "CORPS NOIR" en fonction de la longueur d'onde (dE(λ,T))/dλ
(5) Déterminer la dérivée de la loi de Planck, et trouver la loi de déplacement de Wien T. λmax = 2.898 m . K/1000
Mettre l´énergie totale rayonnée par le corps noir sous la forme:

Le rayonnement solaire et le corps noir et le spectre solaire
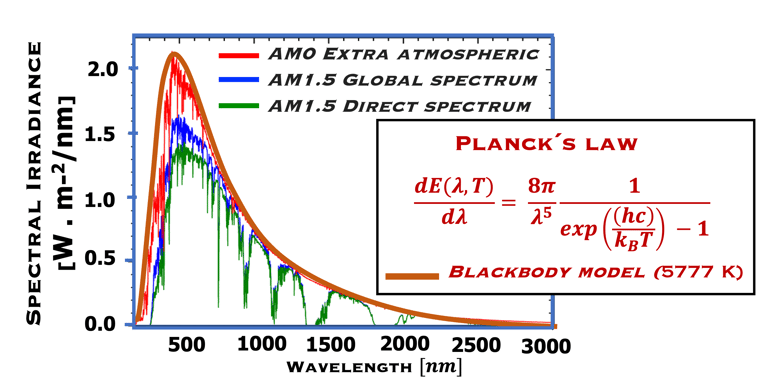
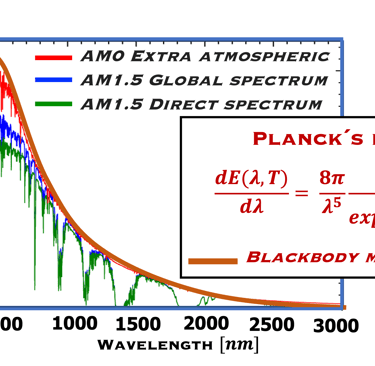
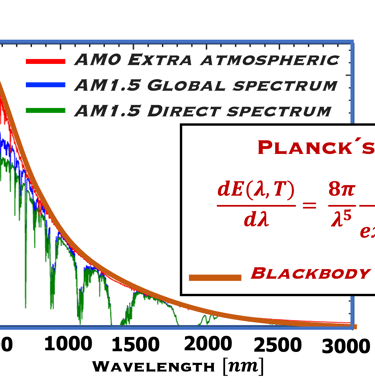
Comparaisons entre l'irradiation spectrale extraterrestre, l'irradiation spectrale normale directe et l'irradiation spectrale totale globale (AM0, AM1.5, and AM1.5G: Air Mass) d'après NREL [https://www.nrel.gov/grid/solar-resource/spectra-am1.5 ], avec le spectre du corps noire à la température du soleil (5777K). AM signifie "Masse Air", c'est la couche atmosphérique que la lumière du soleil doit traverser. Noton que le spectre solaire comprend les Ultraviolets: 0.20 – 0.39 µm, la lumière Visible: 0.39 – 0.78 µm, le spectre Infrarouge proche: 0.78 – 4.00 µm, et l´Infrarouge: 4.00 – 100.00 µm
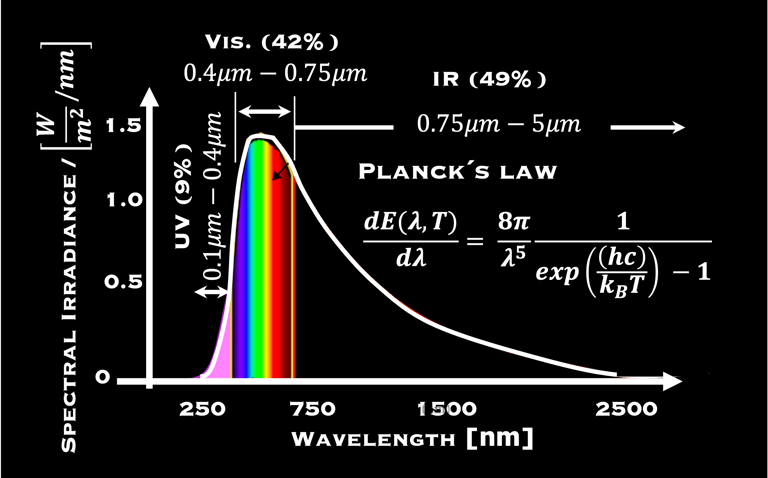
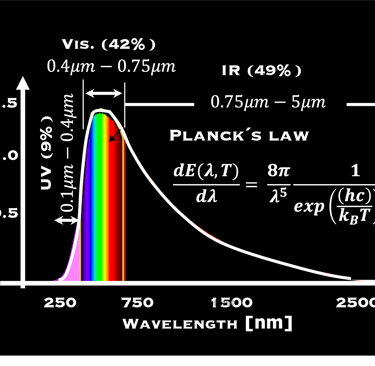
Densité de puissance rayonnée du soleil
Imaginer le soleil qui émet sa puissance dans toutes les directions de l'espace d´une manière uniforme
Chaque mètre carré du Soleil émet une quantité d'énergie donnée par la loi de Stefan.
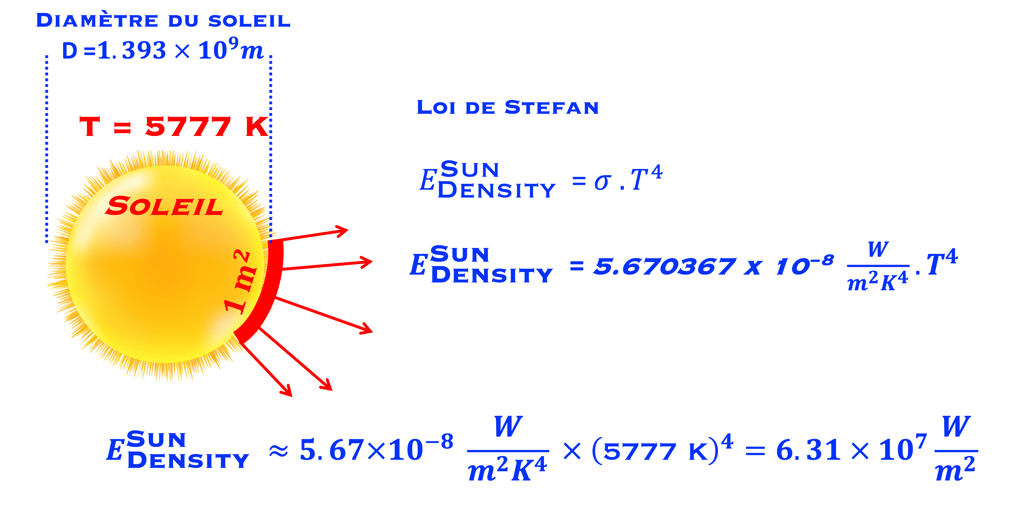
Considérons le soleil comme un objet sphérique de rayon RSoleil et calculons l'énergie totale émise par le soleil
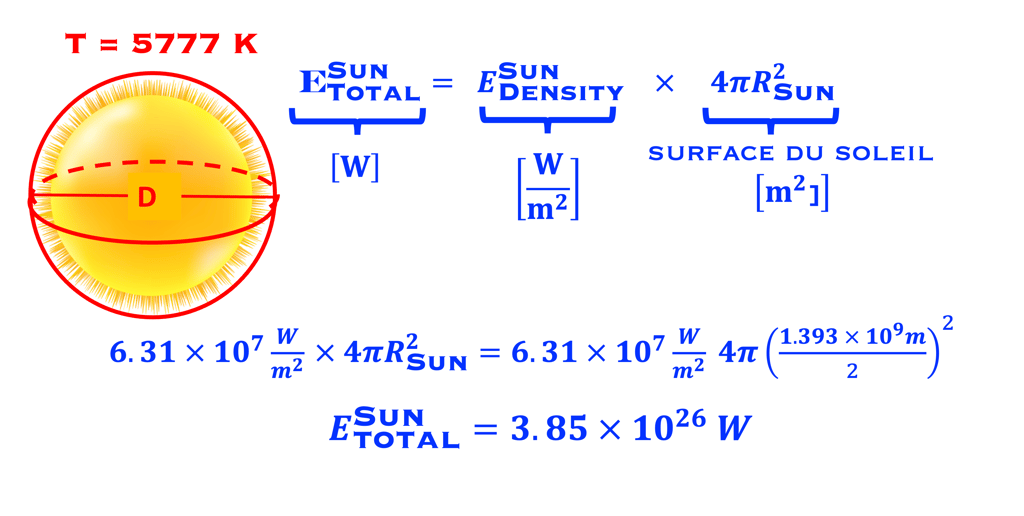
Combien d´énergie reçoit la terre ?
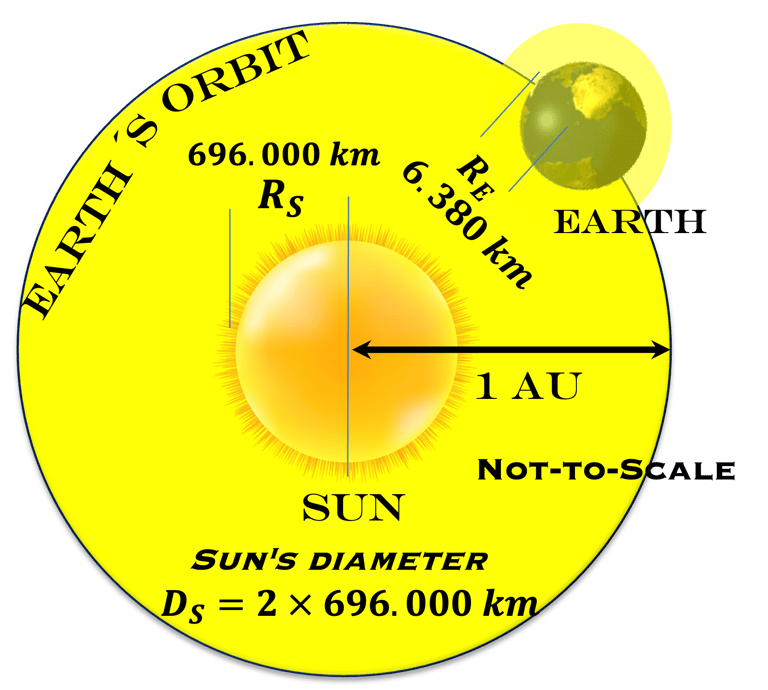
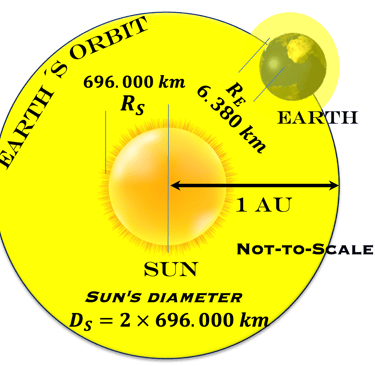
Nous considérons une sphère à la distance RS-E , comme le montre la figure
La surface de cette sphère est:
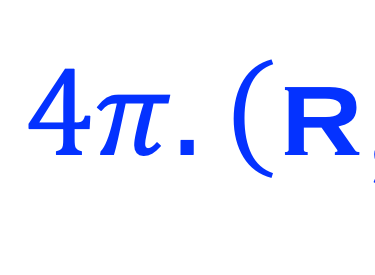
La densité de puissance rayonnée par le soleil est uniformément répartie sur S
Le soleil rayonne par unité de temps par unité de surface à la distance de la Terre RS-E une quantité d'énergie connue sous le nom de "constante solaire, S"


N-B dans tout ces calculs on a pas tenu compte de l'atmosphère
Quelle est la fraction de la constante solaire qui frappe la Terre ?
Nous supposons la terre comme un objet sphérique de rayon RE
La puissance lumière qui tombe sur la terre est répartie d´une manière homogène
Nous devrions chercher la quantité qui traverse un disque comme le montre la figure, alors la fraction qui arrive sur la terre est:




Ce qui correspond à une moyenne annuelle d'environ:

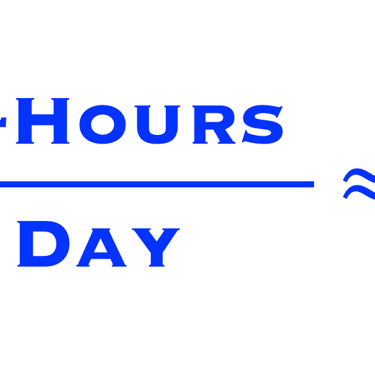
Effet de l'atmosphère
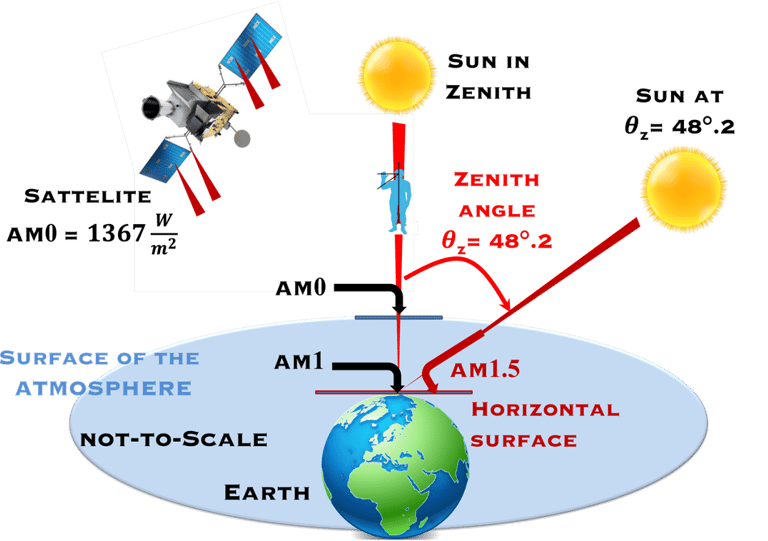
Les rayons du soleil doivent traverser une grande quantité de masse d'air avant d'atteindre la surface de la terre.
Les gaz et particules présents dans l'atmosphère absorbent et diffusent respectivement les rayons lumineux
Les gaz présents dans l'atmosphère sont principalement la vapeur d'eau, l'ozone, le dioxyde de carbone et l'oxygène
Chaque gaz absorbe certaines longueurs d'onde, en émet d'autres et en laisse passer d'autres avec une signature spectrale spécifique
La bande d'absorption de l'ozone (𝐎𝟑) se situe dans les régions ultraviolettes et visibles du spectre solaire. La vapeur d'eau (H𝟐O) et le dioxyde de carbone (CO𝟐) absorbent dans l'infrarouge proche jusqu'au rouge des régions spectrales
Ce sont ces interaction atmosphériques qui réduisent la puissance solaire qui atteint la surface de la terre
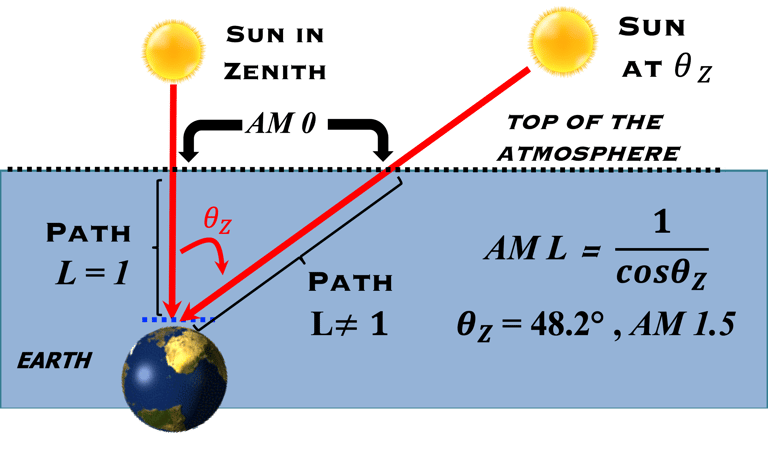
La Masse d'Air » en anglais Air Mass (abrégée AM) mesure la quantité d'atmosphère que la lumière du soleil doit traverser
La relation mathématique entre la masse d'air et l'angle solaire est donnée par la formule la plus courante AM L = 1/cos𝜽𝒛
Pur le soleil au zenith lorsque la lumière du soleil est directement au-dessus de la tête (𝜽𝒛 = 0°, AM1)
Toute masse d'air supérieure à AM1 nous indique combien de fois plus d'atmosphère la lumière du soleil doit traverser par rapport à la situation au zenith, par exemple (𝜽𝒛 = 48.2°, AM1.5)
Lorsque le soleil atteint l'horizon, (𝜽𝒛 = 90°, au coucher du soleil) La
Reference: https://www.pveducation.org/pvcdrom/properties-of-sunlight/air-mass
F. Kasten, A.T. Young, Revised optical air mass tables and approximation formula. AppliedOptics [Internet] ; 28, 4735–4738, 1989
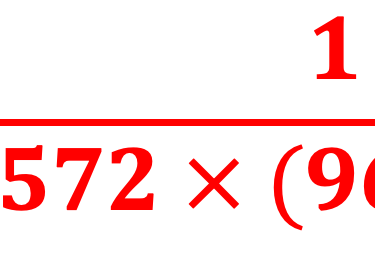

AM0 est le spectre à l'extérieur l´atmosphère qui signifie Air Mass 0, La puissance mesurée hors atmosphère est la constante solaire démontrée plus haut
Le spectre AM0 est utilisée pour tester les performances des cellules solaires dans l'espace,
On peut distinguer deux spectres AM1.5:
AM1.5D: Direct Normal Irradiance (DNI)
AM1.5G: Global Horizontal Irradiance spectrum (GHI), ce spectre est généralement utilisé pour tester les performances des cellules solaires terrestres
Le rapport de masse de l'air (AM) montrant que plus le rayonnement solaire traverse une couche épaisse de l'atmosphère, plus il est réduit. La figure indique AM0 à l’extérieur de l´atmosphère et AM1.5 sur la surface de la terre
Spectre d'irradiance solaire AM0 au sommet de l'atmosphère (courbe rouge) et AM1.5 au niveau de la mer (directe en vert et globale en bleu). La courbe rouge briquer eprésente le spectre d'un corps noir à 5 777 K incluant la loi de Planck(en longueur d'onde) du corps noir
Effet de l'atmosphère et relation avec les cellules photovoltaïques
Adapté de « cours de Prof. Bruce M. Clemens, Stanford University, Autumn 2013 ».
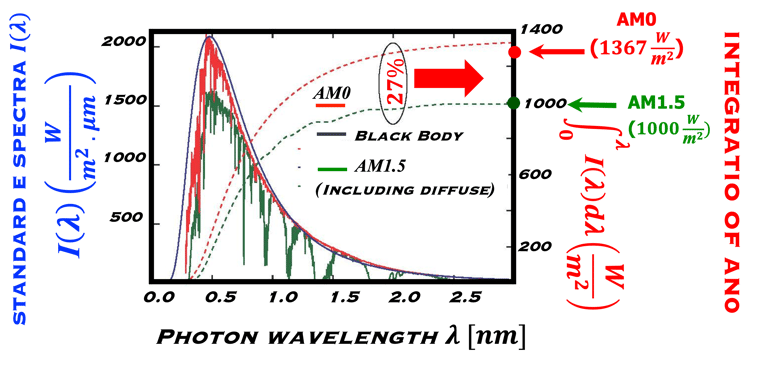
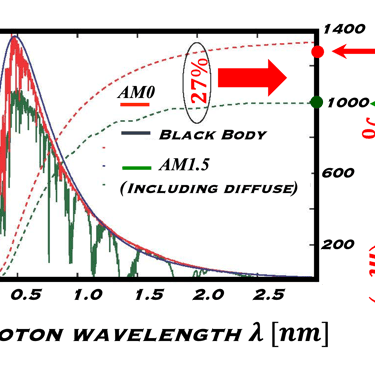
Lorsqu'on intégre le spectre standard AM1.5 et AM0 sur la longueur d'onde longueur d'onde on trouve la densité de puissance
Pour AM0, nous obtenons 1367 W/SQM
Pour AM1.5, nous obtenons 1000 W/SQM
La réduction relative due à l'atmosphère pour AM1.5 est:
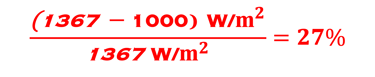

Schéma illustrant les différentes formes de rayonnement tombant sur une surface ou sur un ensemble de module photovoltaïque

Si l'atmosphère n'existe pas nous allons recevoir sur terre Le spectre AM0 c'est à dire environ 1370 W/sqm
Ce nés pas le cas car l'atmosphère terrestre interagit avec le rayonnement solaire incident comme le montre la figure ci-dessous:
le faisceau direct
le rayonnement diffuse
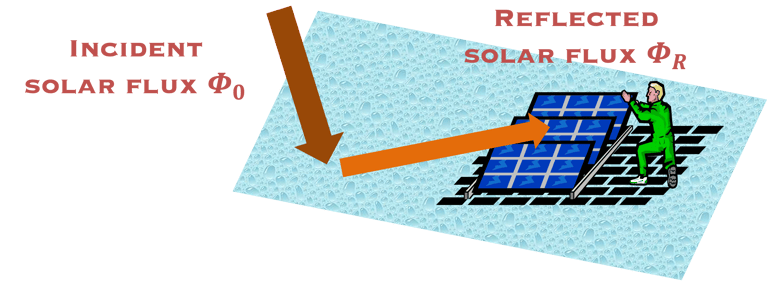
le rayonnement réfléchi par le sol (Albedo) (ΦR/Φ0 [%] is the albedo which is the fraction of the solar radiation flux reflected by a surface)
The earth has an average albedo of about 30% i.e. of the solar radiation is reflected by the earth and sent back into space.
The albedo is not the same on the whole earth
Le rayonnement absorbé est principalement le facteur influençant la production d'énergie d'un système photovoltaïque
Le flux absorbé de photons dépend du rayonnement incident, de la masse d'air et de l'angle d'incidence
Les données précises sur l'irradiation de la surface solaire sont une condition préalable à la planification et à l'exploitation efficaces des systèmes photovoltaïques
Lorsqu'on intégre le spectre standard AM1.5 et AM0 sur la longueur d'onde longueur d'onde on trouve la densité de puissance
Pour AM0, nous obtenons 1367 W/SQM
Pour AM1.5, nous obtenons 1000 W/SQM
La réduction relative due à l'atmosphère pour AM1.5 est:
Il est important de bien connaitre comment calculer
Photon flux density and power density vs. band gap energy


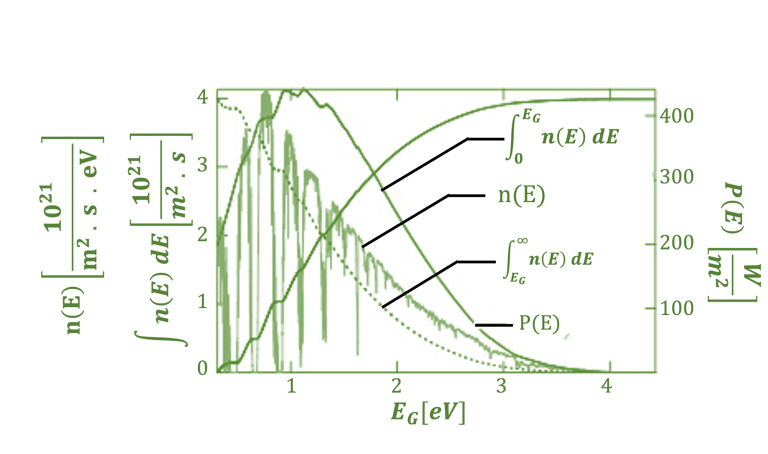
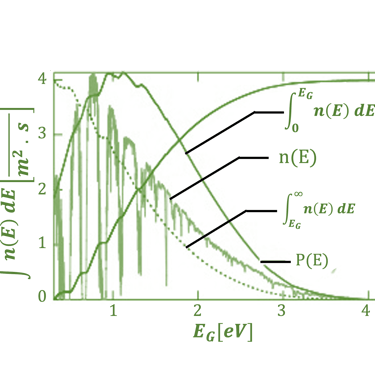
Le flux total de photons au-dessus de la bande interdite d'un matériau est le flux de photons qui est absorbé et génère des électrons
L'intégration de n(E) permet de calculer le flux de photons au-dessus de chaque énergie de bande interdite
Si nous supposons que chaque photon au-dessus de la bande interdite génère un électron dans le matériau qui contribue au courant, nous pouvons calculer le courant total généré par la lumière en fonction de la bande interdite.

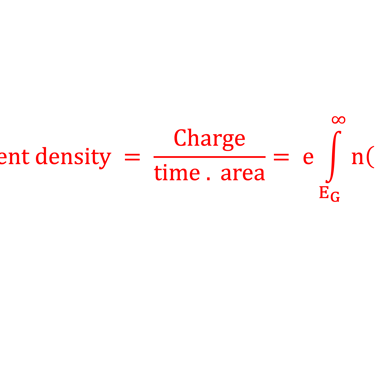
La question principale que nous aborderons tout au long de ce cours porte sur le rendement d'une cellule, qui est la puissance de sortie de la cellule solaire divisée par la puissance délivrée par le flux de photons ?
Pour convertir la densité de courant en densité de puissance, nous devons connaître la tension à laquelle les électrons sont extraits.
Dans une cellule solaire réelle, cette tension notée Voc est calculée à partir d'une courbe I-V que nous allons établir tout au long de ce cours
Nous supposons que cette tension est égale au maximum (dans les meilleurs des cas) à la bande interdite (Max. EG), alors:


Le maximum est atteint pour une bande interdite de 1,122 EV et 490 W/sqm
La puissance d'entrée étant de 1000 W/sqm (AM1.5, conditions standards ), le rendement est de 49%
Simulation et mesure du rayonnement solaire

On peut reproduire au laboratoire toutes les conditions STC, i.e. un ensoleillement instantané, une température de 25°C et utiliser des filtres pour assurer les conditions Air-Masse de 1,5, et 1.5G
Pour simuler le rayonnement solaire AM1.5 , il faut combiner deux sources artificielles de lumière une lampe de Tungstène (W) et une lampe de Xénon (Xe), une optique composée de lentilles et filtres, un collimateur et un intégrateur d'uniformité de faisceau
Il faut aussi disposer d´une cellule de référence calibrée pour mesurer l´intensité de la lumière avant toute utilisation pour mesurer par exemple les caractéristique courant-Tension des cellule solaire à étudier
La température de la cellule est contrôlée par un système de refroidissement pour maintenir à une valeur fixe la température pendant le déroulement des mesures
Les simulateurs solaires de classe AAA sont certifiés conformes aux normes ASTM E927, IEC 60904-9 et JIS C 8912 pour les performances de et correspondent au spectrale de longueur d'onde 400-1100 par Incréments de 100 de largeur de bande
Pour les grandes surfaces et un nombre de module assez important, l´industrie utilise des Simulateur solaire type flash:
Nous revenons sur les détail pendant les cours sur les cellules solaires et les mesures des caractéristiques courant-tension
Quelques informations utiles /
CEI (Commission électrotechnique internationale) et l'ISO (Organisation internationale de normalisation) travaillent ensemble à la normalisation de la mesure électrique et électronique
La norme CEI60904 décrit les procédures de mesure des performances des PV, telles que les caractéristiques courant-tension, sous la lumière naturelle ou simulée du soleil
Les simulateurs solaires doivent fournir les conditions des normes du spectre solaire établies par la CEI et l'ISO, telles que AM1.5G (l'irradiance globale) qui atteint la surface de la terre à une masse d'air de 1,5 avec une valeur d'environ 1000 W/m²
Le pyranomètre
Le pyranomètre est un élément essentiel pour de mesurer la densité du flux de rayonnement solaire en ou l'énergie solaire qui atteint la surface de la Terre ou votre module photovoltaïque installé sur le toit de votre résidence Techniquement,
Il est conçu pour mesurer l’irradiance solaire horizontale totale (en anglais : Global Horizontal Irradiance GHI), reçu sur une surface horizontale composée de : DNI (en anglais : Direct Normal Irradiance) et DHI (Diffuse Horizontal Irradiance)
La réponse d'un pyranomètre par temps clair est maximale à midi lorsque le soleil est à son point le plus haut, elle est minimale au levé et couché du soleil lorsque le soleil est à l'horizon
GHI = DHI + DNI . cosθz θz est l´angle par rapport au zénith
Les mesures des pyranomètres professionnels peuvent s´étendre sur toutes les longueurs d'onde de 210nm à 3600nm , avec un angle d'ouverture de 180° avec une sensibilité de μV/W/m², une Linéarité qui peut atteindre jusqu´à des valeurs 2800 . Le temps de réponse est d´environ : 10 s – 40ms
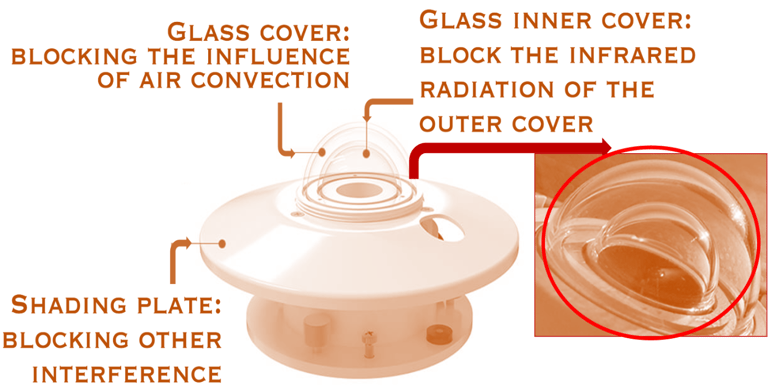
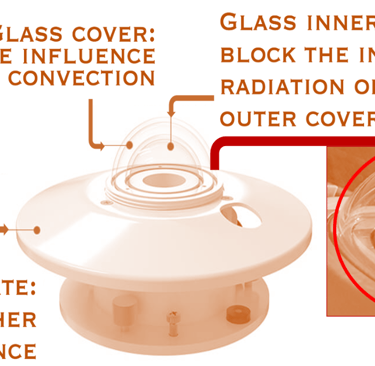
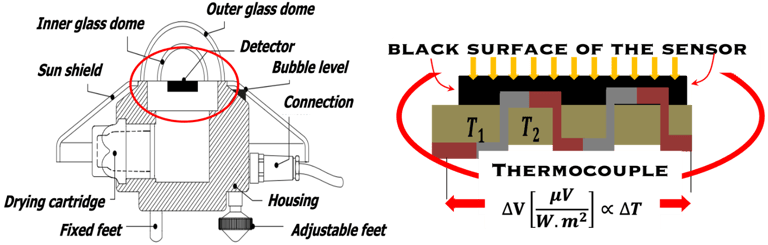
Nous décrivons ici les pyranomètres à thermopile qui utilisent un ensemble de thermocouples, qui détecte une différence de température entre deux surfaces, comme c´est montré sur la figure ci-dessus: la surface active (dite chaude) horizontale exposée au soleil et l´autre considérée comme référence (dite froide). La surface chaude, (un corps noir) est protégée par un dôme en verre ou en quartz sauvent en double isolation
La surface noire (corps noir) se chauffent et un gradient de température ∆T induit un signal électrique, ou différence de potentiel, proportionnel au gradient de température entre la surface noire et une surface de référence ∆V en [μV/W/m²] ∝ ∆T
Les Pyranomètres sont munis d´un dôme qui les protège contre la poussière, l'humidité, le vent et tout ce qui peut empêcher la détection de l'irradiation
Source utile: https://www.hukseflux.com/uploads/inline/note-pyranometer_physics_why_two_domes_v2004.pdf
pyrhéliomètre
Pour mesurer sélectivement l’irradiance solaire directe (DNI), on utilise un capteur spécial, le pyrhéliomètre basé sur le même principe que le pyranomètre un capteur de réponse thermique rapide
Les pyrhéliomètres fonctionnent dans un intervalle de 200 à 4000 nm et fonctionne dans ses conditions extrêmes de températures allant de -40°C et jusqu`à +80°C.
La différence avec un pyranomètre c´est l'angle d'ouverture de 5°, (alors qu´un pyranomètre collecte le rayonnement sur 180°), de sorte que seul le rayonnement direct entre dans l´ouverture du pyrhéliomètre qui doit être pointé constamment vers le soleil comme le montre la figure ci-dessous


Double dôme
Comparison des deux instrument de mesure du rayonnement global (pyranomètre) et directe (pyrhéliomètre). La video explique trés bien l'usage de ces instrument dans un champ de panneaux photovoltaics
Illustration d´un pyranomètre montrant le corps noir essentiel pour la collection des radiations. Une série de thermocouples transforme le gradient de température en signal électrique. Le double dôme offre une meilleure protection contre les échanges thermiques infrarouges
la bancabilité
la "bancabilité" signifie que les financiers (les banques) sont prêts à investir dans une technologie solaire parce que les données solaires indiquent la qualité et la durabilité et la guarantie à long terme de cette technologie sont garanties
Exemple de scénario : Imaginez un groupe de particuliers qui envisageant d´installer un système solaire sur le toit de leur résidence, ils doivent établir un modèle financier :
Estimer la production d'énergie (en fonction de l´emplacement et la technologie choisie)
Calculez les coûts initiaux (panneaux, onduleurs, installation)
Connaitre sa consommation électrique à cour moyen et long terme
Évaluez la période de récupération ( payback time)
Deux technologies CSP (concentrated Solar Power) et CPV (Concetrated Photovoltaics) ustilise DNI (Direct Normal Irradiation).
DNI est s´environ 2 635kWh/m²/année dans le site de Ouarzazate et c´est l'une des zones les plus ensoleillées au monde qui peut rassembler les trois technologies CSP, CPV et PV (Photovoltaics)
L'un des défis les plus importants pour l'énergie solaire à Ourzazate est la consommation d'eau pour le complexe Noor à Ouarzazate, estimée à 2.5-3 millions de m³ par ans* pour le refroidissement humide (Noor I, II, III)
Considérations générales
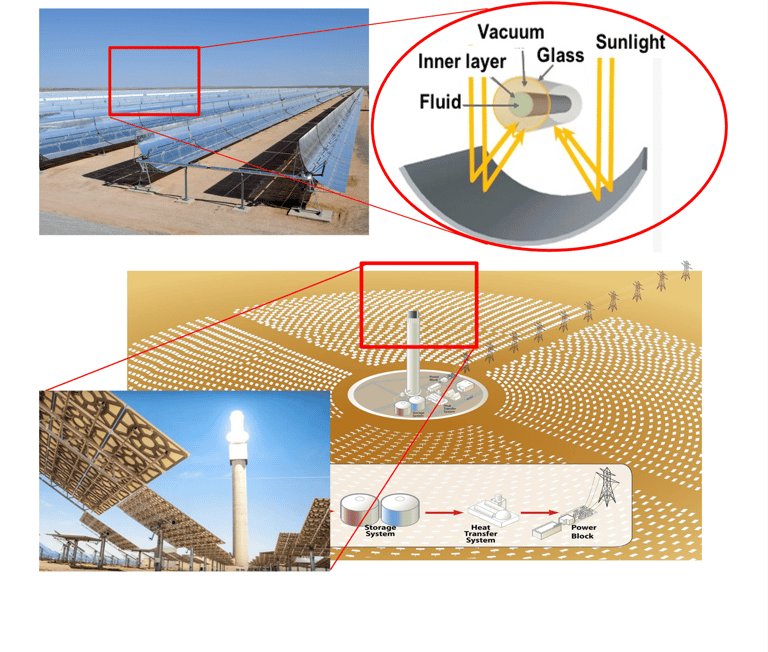
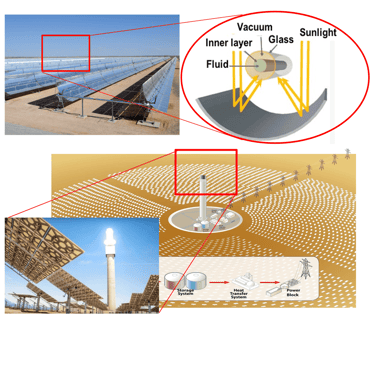
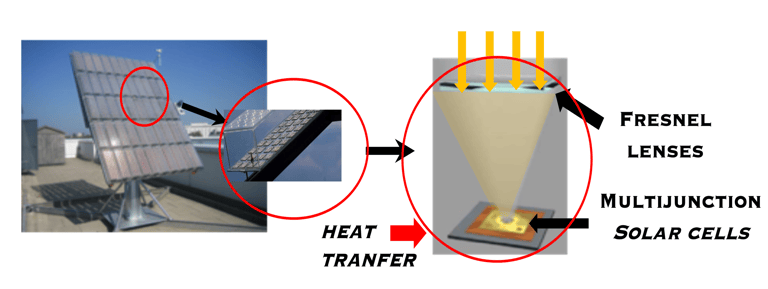
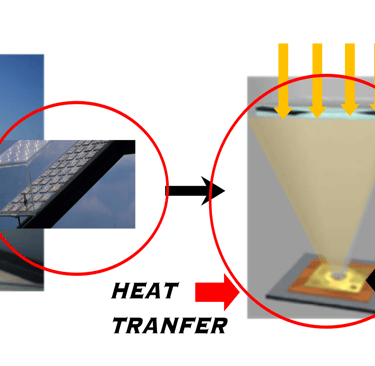
Illustration des technologies CSP et CPV; voir détails dans les liens: https://www.solarpaces.org/worldwide-csp/csp-projects-around-the-world/ (https://www.ise.fraunhofer.de/en/press-media/press-releases/2013/world-record-solar-cell-with-44-7-efficiency.html )
Nous aurons l'occasion de discuter en détail dans les séminaires sur les technologies PV les paragraphes suivants:
Plane-of-array irradiance: L'irradiation solaire globale atteignant les modules PV inclinés est appelée (Plane-of-array irradiance (POA), ce paramètre est -largement utilisé dans l’analyse de la performance et la modélisation de modules PV
L’irradiation solaire sur un plan inclinée (Plane-of-array irradiance) est une combinaison de rayons solaires directs, d'irradiation diffuse et d'albédo
L'albédo est très important dans le cas des modules bifaciaux, car il influe énormément la performance des panneaux bifaciaux, qui captent la lumière solaire des deux faces supérieure et inférieure etpeuvent produire de l’électricité en utilisant la lumière réfléchie en plus de la lumière directe du soleil
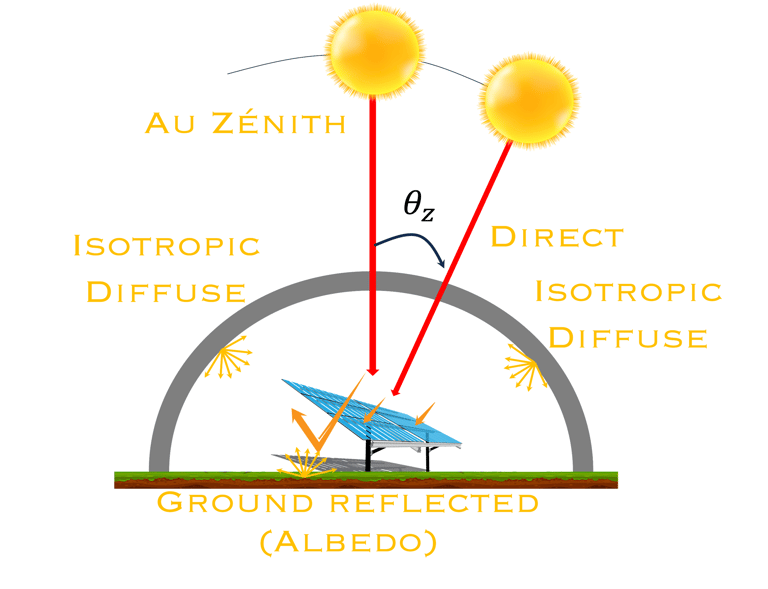
Nous recommandons de regarder un model présenté par Beyza Durusoy dans un article sur Scientific Reports qui traite l'irradiation sur un module PV incliné est divisée en trois composantes:
Le rayonnement (isotrope) après diffusion par l'atmosphère
Le rayonnement direct sans diffusion par l'atmosphère
Le rayonnement réfléchi par le sol.
Bif(POA) = G(DIRECT) + G(DIFFUSE) + G(REFLECHI-FACE) + G(REFLECHI-ARRIÈRE)
Je renvoie le lecteur sur cet article intitulé : Solar irradiation on the rear surface of bifacial solar modules : a modeling approach : https://www.nature.com/articles/s41598-020-70235-3
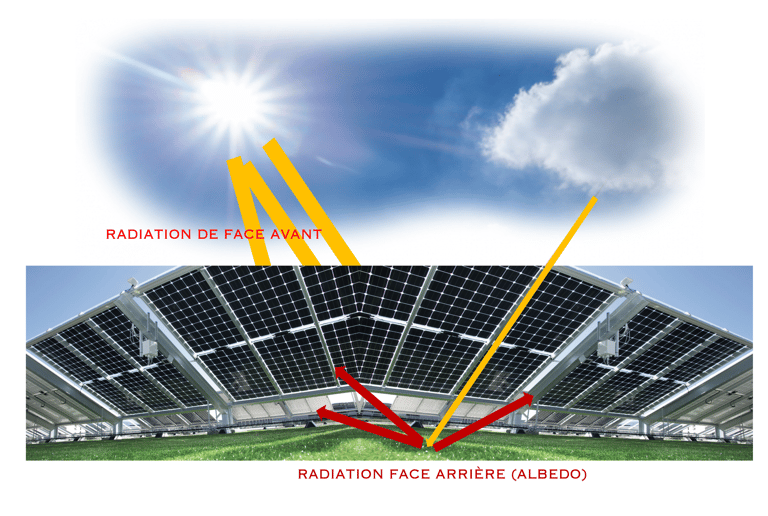
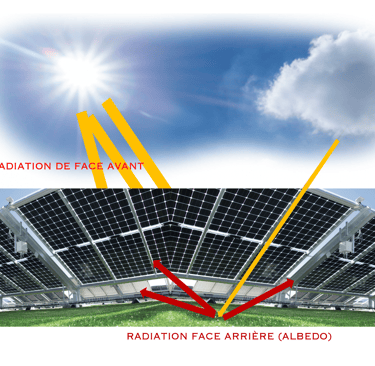


système de panneaux solaires PV basé sur la technologie bifaciale avec la face arrière qui absorbe la lumière réfléchie par le sol ou albedo, 5 à 15%). A gauche la technologie bifaciale en Agri-PV
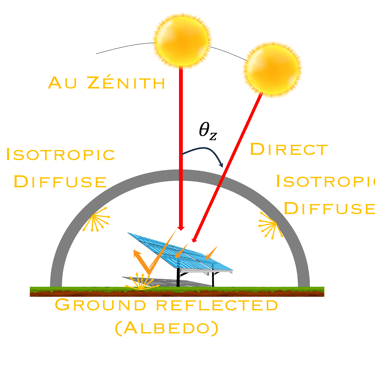
Projet: Performance, modélisation et simulation des systèmes bifaciaux, évaluation comparative et bancvabilité
Benchmarking) des technologies dans les zones désertiques comme Laayoune (à suivre)
Un projet intéressant et qui n´est pas assez exploré, consiste à générer des données réelles sur le terrain afin de quantifier et de caractériser les taux de dégradation des systèmes photovoltaïques bifaciaux, étant donné le manque de données en général. Il s'agit d'exposer un système photovoltaïque à modules bifaciaux au rayonnement dans votre établissement et d'effectuer des mesures et des modélisations. Identifier les comportements de défaillance potentiels sur le terrain et explorer la dégradation de la face avant et de la face arrière qui peut se produire à des rythmes différents. Comparer les systèmes bifaciaux avec lesautres technologies photovoltaïques. Explorer les performances avec et sans suiveurs (Trackers)
Bilan énergétique du système " Terre-Atmosphère-Soleil " en se basant sur la loi de Stefan- Boltzmann et de Wien
Dans ce qui suit, nous allons établir un modèle basé le corps noir en supposant qu'une partie de l'énergie du soleil est réfléchie/absorbée par l'atmosphère et le sol.
Les radiations solaires arrive au sol et le réchauffe, qui à son tour renvoie une puissance radiative (Infra-rouge) vers l’espace
Les rayon infrarouges sont bloqués dans l’atmosphère à cause de l´accumulation des gaz à effet de serre qui réchauffe encore d´avantage la terre
Nous étudions la température de la terre d´une manière simple en assimilant la terre, l´atmosphère à des corps noir
Nous établissons le bilan énergétique du système " Terre-Atmosphère-Soleil " en se basant sur la loi de Stefan- Boltzmann et de Wien
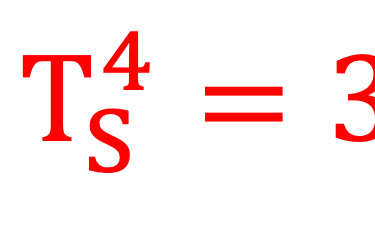
la terre se réchauffe et émit un flux ΦT dans l´infrarouge
Dans ce qui suit nous allons envisager et discuter différents scénarios et discuter la température de la terre suivant l´hypothèse utilisée

La loi de Wien permet de montrer que Le soleil émit un flux ΦS dans le visible donné par la relation ci-dessous où λMax est en μm Et la température T en K

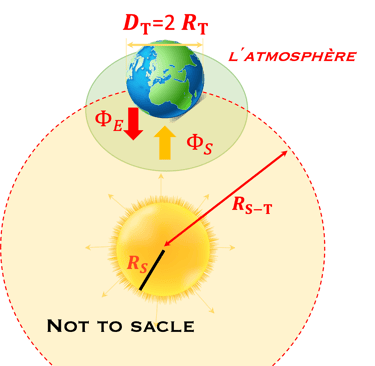
Nous avons vu dans ce cours que le soleil émit dans toutes les directions une puissance totale PS calculée par la loi de Stefan ci-dessous: (dans cette relation RS est le rayon du soleil et TS sa température. PS est répartie d´une façon homogène sur la surface d´une sphère de rayon R(soleil-Terre)=RSE
Cette relation assimile le soleil à un corps noir dont l´énergie par unité de temps et unité de surface est proportionnelle à sa température TS à la puissance quatre
Position du problème:
Nous Considérons différents scénarios:
I. Bilan sans l´atmosphère et sans Albedo
II. Bilan sans atmosphère mais avec albedo
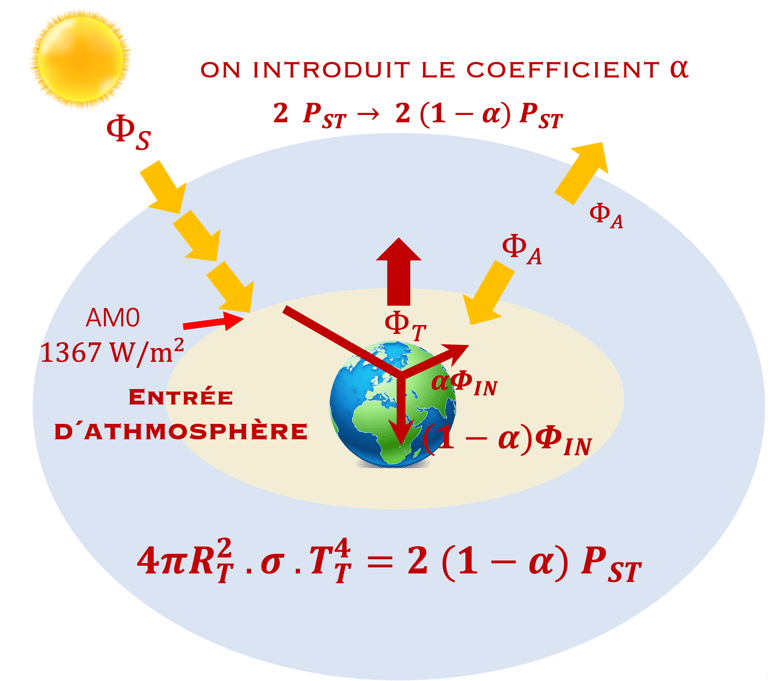
III. Bilan avec atmosphère mais sans albedo
IV. Bilan avec Albedo et atmosphère (atmosphère transparent)
V. Bilan avec Albedo et atmosphère (atmosphère partiellement transparent)
I. La première hypothèse suppose que le rayonnement solaire arrive sur la terre sans aucun obstacle (sans atmosphère" et sans l´Albedo)
Rappelons encore que PS est répartie une sphère de rayon RSE et seule la partie qui traverse un disque de rayon RT atteindra la surface de la terre.
Nous notons PT la portion de PS qui arrive sur terre, en faisant une "règle de trois" , on obtient:
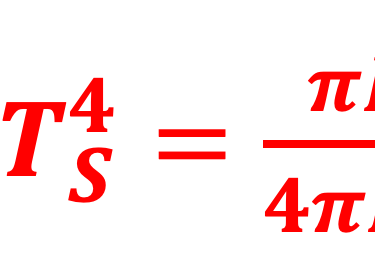
N-B:
Ce flux réchauffera la terre qui atteidra une température moyenne T1,
Il peut aussi être utilisé pour produire de l´électricité verte si on place des panneaux solaires à surface de la terre
Ce flux sera de toute évidence réduit par la présence de l´atmosphère
Comme nous l'avons fait pour le soleil, nous assimilons la terre à un "corps noir" à la température T1
La puissance rayonnée par la terre à la température T1 est selon la loi de Stefan:


"On en déduit la température de la terre"
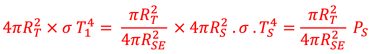
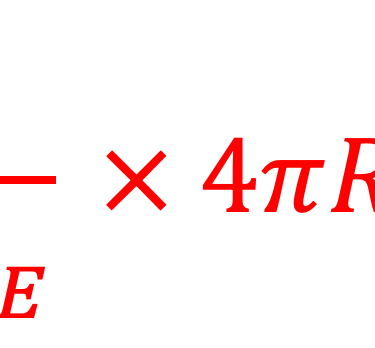
Le bilan énergètique ΦIN = ΦOUT (flux entrant = flux sortant) impose

On vous conseille de faire l'application numérique, on trouve T1 = -7°C
Avec une telle hypothèse la terre est très froide". Ce modèle sans atmosphère et sans albdo va nous servir de base pour l´améliorer et s´approcher de la réalité


II. Cas "sans atmosphère" mais avec Albedo
On aura le bilan énergétique suivant:
Quiz – faire une analogie avec la relation de base (I.1) et en déduire la valeur de la température de la terre dans cette l'hypothèse II
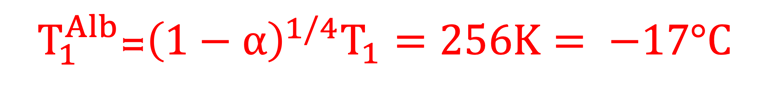
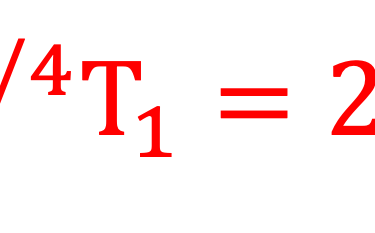
Remarque l´hypothèses II ne sont pas suffisante pour s'approcher de la réalité, on doit tenir compte de l´atmosphère et de l´albedo, y compris d´autres paramètres que l´on étudiera dans ce qui suit
III. Le bilan avec seulemt l´atmosphère
On va utiliser l'hypothèse que La terre entourée d´une atmosphère
nous assimilons la terre et l´armosphère à des corps noires à T = 300 Kelvins.
Le lecteur peut appliquer la loi de Wien et montrer que la terre émit un maximum de rayonnement dans l´IR (10 μm), et l´atmosphère émit dans
le visible (0.5 μm)
La différence entre les deux maxima λMax-T= 10 μm et λMax-S = 0.5 μm fait que l´atmosphère est transparent au rayonnement solaire

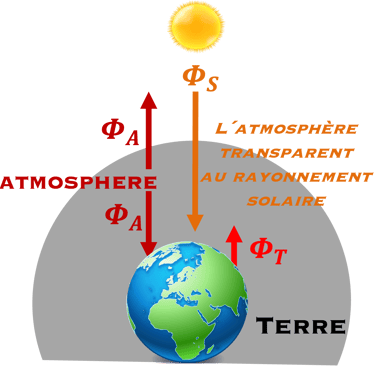
Notations (voir sur la figure)
N1: L´atmosphère recevra (ΦT ) de la part de la terre
N2: L´atmosphère émettra (ΦA ) vers la terre et (Φ_A ) vers l´espace
N3: La terre recevra (ΦA ) de l´atmosphère
N4: La terre recevra ΦS du soleil
N5: La terre émettra ΦT vers l´atmosphère
En tenant compte de N1et N2 le Bilan de L´Atmosphère s'écrit: ΦT = 2ΦA (III.1)
N3, N4 et N5 donne Bilan de la terre: ΦA + ΦS = ΦT (III.2)
Nous éliminons ΦA entre (III.1) et (III.2), il vient: ΦT = 2ΦS (III.3)
(III.3) montre que la présence de l´atmosphère double la puissance à la surface de la terre
Notons T3 la température dans ce cas de la présence de l´atmosphère, alors Le bilan énergétique revient à apporter une petite modification au modèle standard sans atmosphère et sans albédo
Cette petite modification au modèle sans atmosphère et sans albédo consists à multiplier la relation établie dans (1) par 2
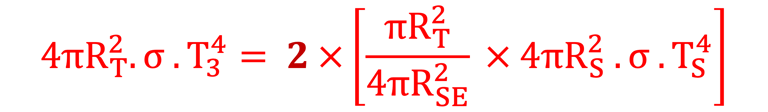
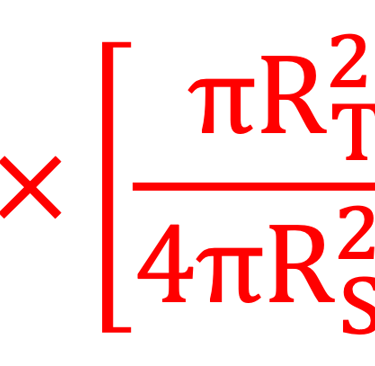
On obtient la température de la terre avec atmosphère mais sans Albédo est:
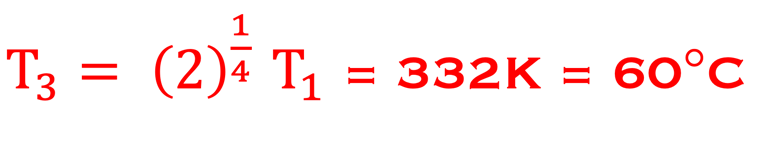
La température de la terre est trop chaude par rapport à la réalité, il est donc certain que nous devrions améliorer nos hypothèses
IV. Le modèle avec Albedo et atmosphère
Nous rappelons ici que l´albedo est la fraction du flux incident réfléchi par la surface de la terre L´albedo est caractérisé par le coefficient, α
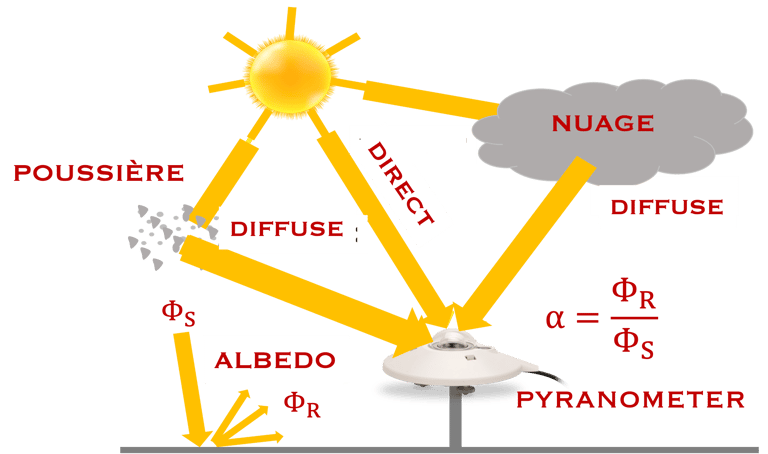
α = 30% du rayonnement est réfléchi par la Terre, le reste 2PS (1-α) est récupérée
Il suffit d´apporter une modification au modèle de base en multipliant par 2(1-α) avec le facteur 2 pour tenir compte de l´atmosphère et (1-α) pour tenir compte de la réfléction sur le sol ( α = 30% pour le sol de la terre). On obtient l'expression suivante et qui aboutit à la température de la terre
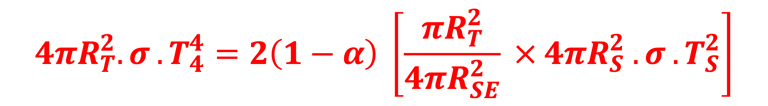
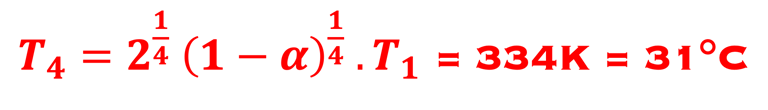
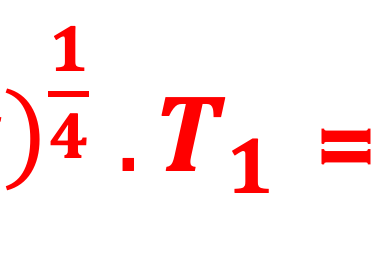
V. Bilan avec Albedo et atmosphère (atmosphère partiellement transparent)
L´atmosphère n´est pas complètement transparent l´atmosphère absorbe une quantité βΦS où 0 < β < 1 et la quantité (1 - β) ΦS va traverser l´atmosphère
Comparons avec l´hypothèse de départ: l´atmosphère qui envoie le flux dans les deux directions: ΦT = 2ΦA (III.1)
"Le bilan de la terre: ΦA + ΦS = ΦT (III.2)
En éliminant ΦA entre les deux équations: ΦT = 2ΦS (III.3)
La modification par absorption de βΦS
Alors:
(III.1) est modéfié et devient: βΦS + ΦT= 2ΦA
(III.2) est modéfié et devient" : ΦA + (1-β) ΦS = ΦT
(III.1) + (III.2) ⇒ ΦT = (2-β)ΦS
Maintenant, partant du bilan de base (sans atmosphère, sans albdo) et introduisons la modification βΦS qui tient compte de ce qui est absorbé par l´atmosphère avec β = 30% alors:
Pour une temérature réalistique de la terre, on doit tenir compte de deux choses:
l´albédo αΦS (réfléchi par la terre)
l´atmosphère βΦS absorbé dans atmosphère

On voit que la température a diminué mais reste encore assez chaude
Regardons ce qui se passe si on laisse l'atmosphère et on enlève l´Albedo?
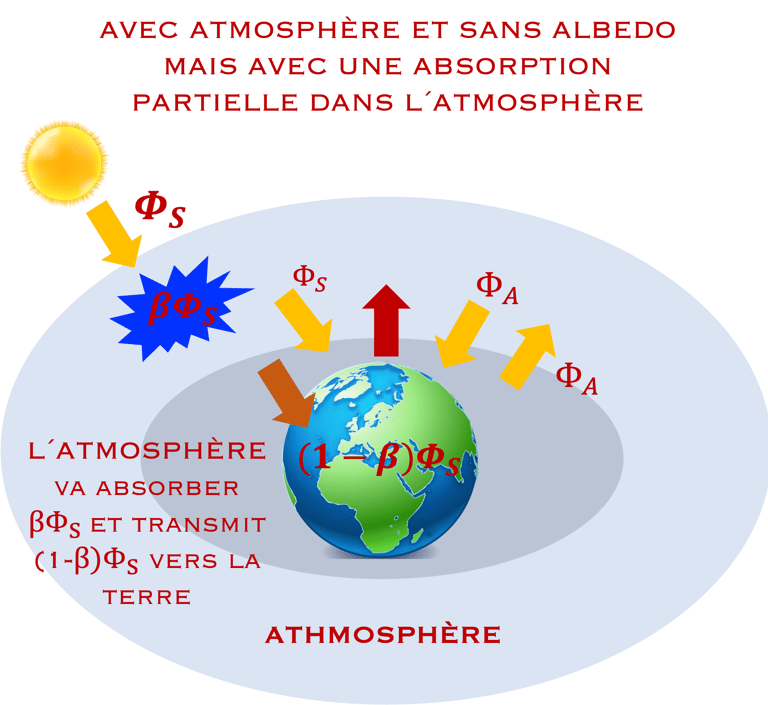
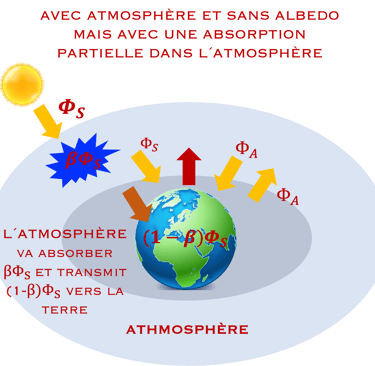
L'atmosphère va recevoir
→ βΦS+ΦT
L'atmosphère reémit 2Φ à la Terre
→βΦS+ΦT = 2ΦA
la Terre recevra ΦA + (1 - β)ΦS
la Terre reémit ΦT
→ ΦA + (1 - β)ΦS = ΦT
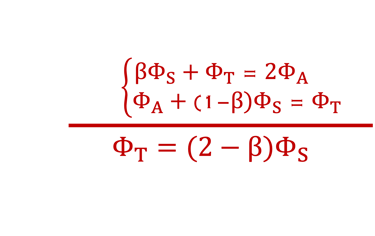
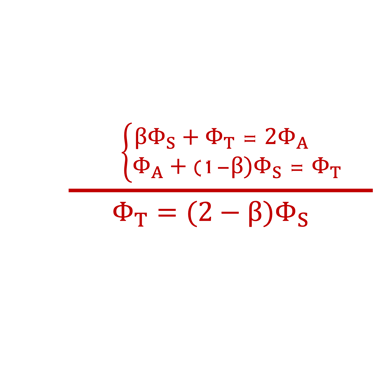
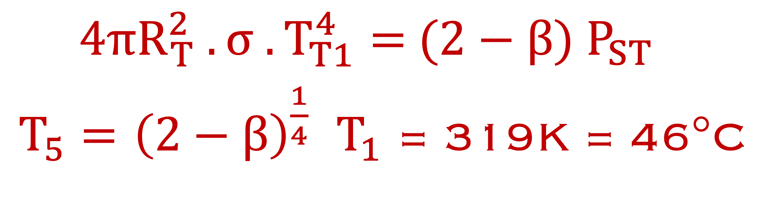
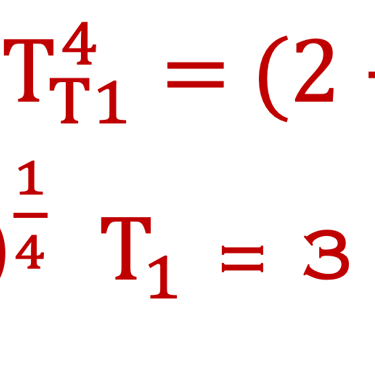
Encore plus chaux, ce qui montre l'importance de l´Albedo
Décrire le schéma ci-dessous illustrant le modèle complet qui tient compte (se servir de la figure ci-dessous) de
Albédo: réflection αΦS
Absorption atmosphérique β ΦS
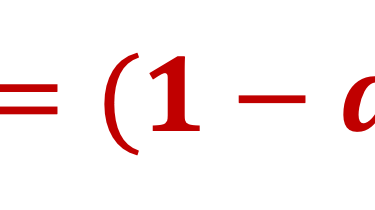
QUIZ - Le lecture peut essayer d´écrire le bilan énergétique et en déduire la température T(α & β) la plus plausible en tenant compte l´albédo αΦS (réfléchi par la terre) et de la quantité βΦS absorbé dans atmosphère.
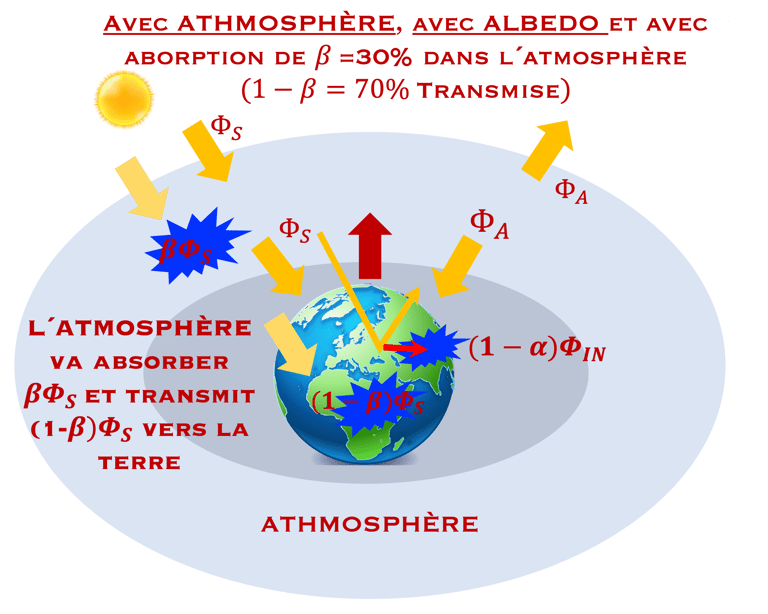
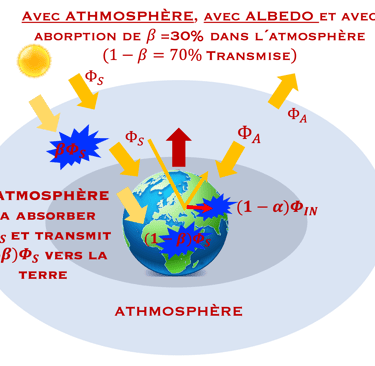
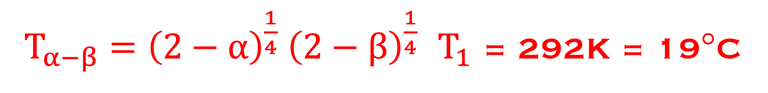
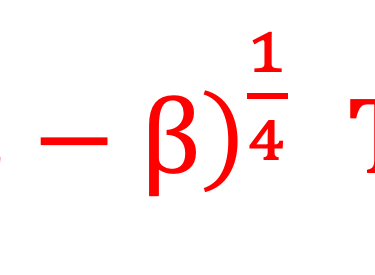
Partir du cas de base (I):
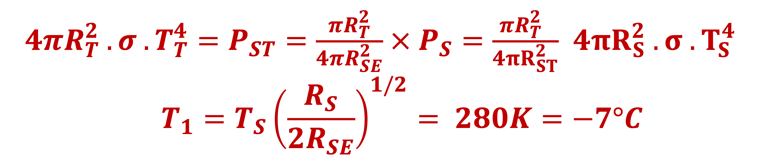
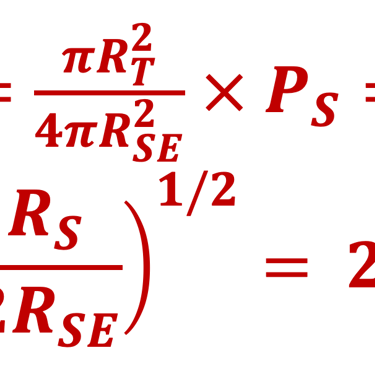
Tenir compte de deux corrections
Correction de l´Albedo
Correction de l'atmosphère (partiel transparence)
On aboutit au résultat suivant:
l’atmosphère (gaz à effet de serre) joue un rôle important dans la régulation du climat, empêchant une large part de rayonnement (rayonnements infrarouges) d’être renvoyée de la Terre vers l’espace. Cela permet à la température moyenne sur Terre d´être vivable environs -19°C dans ce model au lieu de -17 °C
Comment maximiser le rayonnement solaire reçu sur un panneau solaire?
Le constructeur donne les caractéristiques d’un panneau photovoltaïque.
Nous retenons ici la puissance du panneau qui s’exprime en "Watt Crète" symbole Wc, ou en "Watt Peak" symbole Wp (en anglais)
Cette puissance est mesurée sous les conditions STC (Standard Test Conditions):
Irradiation incidente maximal : Air Mass 1.5 (1000 W/m²)
Température du panneau de 25°C
Dans cette partie on ne parlera que de la puissance du panneau (ici nous choisissons 240Wc sur le tableau ci-dessous), les autres caractéristiques dans le tableau seront traitées dans une autre section
Regardons le panneau PV de puissance maximale 240W sous les conditions STC
Si les radiations incidente sur le panneau est de 1 kW/m² , alors la puissance instantanée en sortie de ce panneau est de 240W
L'illustration (à gauche) montre une courbe courant tension d'un panneau photovoltaïque typique avec tous les paramètres électriques mesurés dans les conditions
Nous revenons sur ce tableau et la caractéristique I-V lors du cours sur la technologie PV et équilibre des systèmes
La question ici comment trouver la bonne inclinaison du panneau solaire pour garantir l'absorption maximale de la lumière incidente tout au long de la journée.
Ceci passe par une connaissance approfondie des angles solaires et des angle horaire du soleil dans un lieu lieu précis
L'angle d'inclinaison optimal d'un panneau photovoltaïque varie tout au long de l'année,
La latitude a un impact sur l'intensité des rayons du soleil qui arrive sur la surface du panneau
Plus la production totale d'électricité du système est élevée et plus le retour sur investissement potentiel est important, alors on doit s'arranger pour que les panneaux solaires reçoivent la lumière directe du soleil le plus longtemps possible au cours d´une journée.
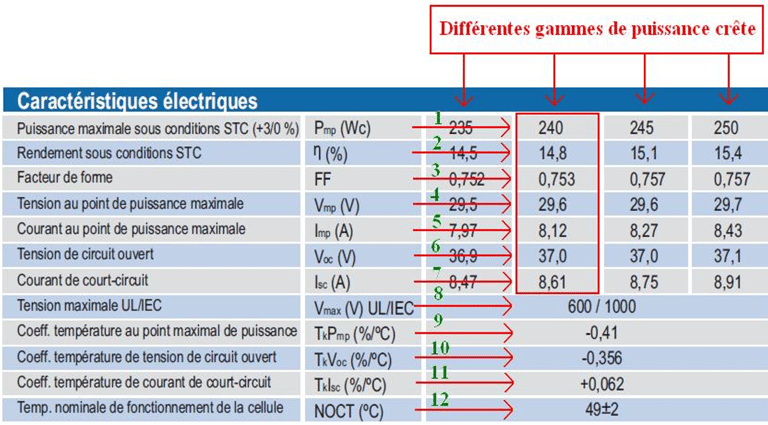
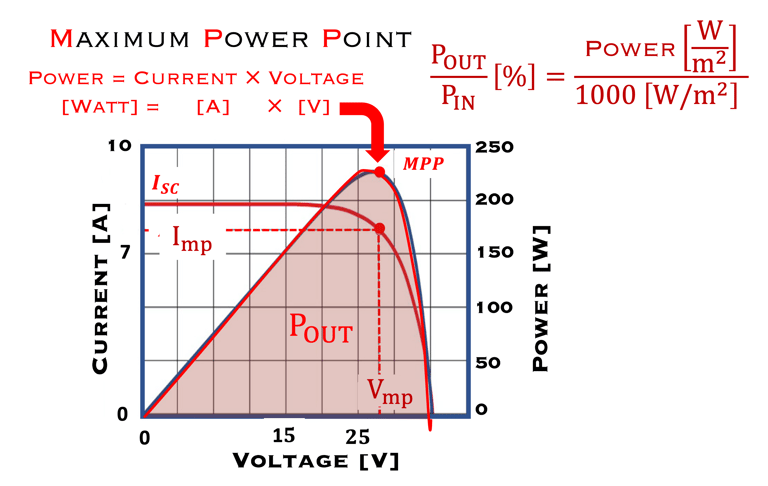
à gauche un exemple de caractéristiques courant-Voltage et de puissance dans des conditions STC (STC = Standard Test Conditions, à savoir 1 kWW/m², température de 25 °C, conditions spectrales Air Mass 1.5 (composition du spectre identique au spectre solaire lorsqu’il traverse une épaisseur et demie d’atmosphère, ce qui correspond à un angle d’incidence de 41.8° par rapport à l’horizontale). à droite la fiche technique délivré par le constructeur et contient toutes les caractéristiques (ici trois panneaux 240W , 245W, et 250W). Nous reviendrons sur toutes les caractéristiques pendant les cours sur l'équilibre des systèmes PV
QUIZ: Considérons l'irradiation solaire quotidienne ou le nombre d'heures pendant lesquelles le soleil brille entre le lever et le coucher du soleil chaque jour ( ou Irradiation solaire quotidienne entre le lever et le coucher du soleil)
Question : Combien de watts votre panneau solaire est-il capable de produire par jour ?
Considérons des panneaux solaires sur un toit (roof top) comme le montre la figure ci-dessous, ils produirons une puissance PSTC dans des conditions idéales (Irradiation incidente maximal : Air Mass 1.5 ; 1000 W/m² , Température du panneau de 25°C ) selon la fiche technique
Sur l'illustration nous avons mis l'angle d'incidence θ, la normale perpendiculaire au panneau, le rayonnement direct, diffuse et l'albédo
Nous répétons encore ici, la puissance nominale, PSTC et le rendement que nous notons (EFF.) "en anglais efficiency" indiquent la quantité de lumière solaire convertie en électricité
Admettons que le propriétaire de cette maison souhaite connaître l'ensoleillement quotidien moyen reçu sur un m² du panneau en 'unité [W/m²].
Supposons que l'insolation maximale d'un jour est de 10 heures (# peak sun hours)
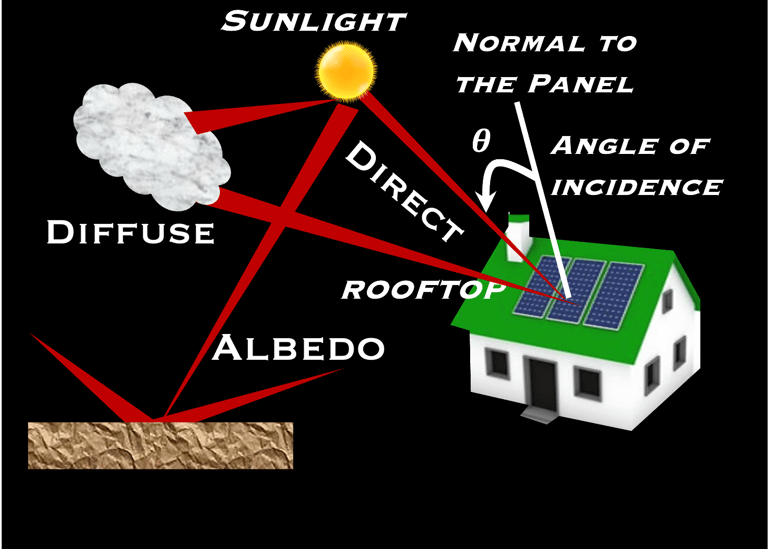
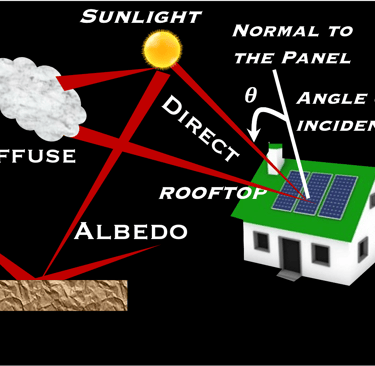
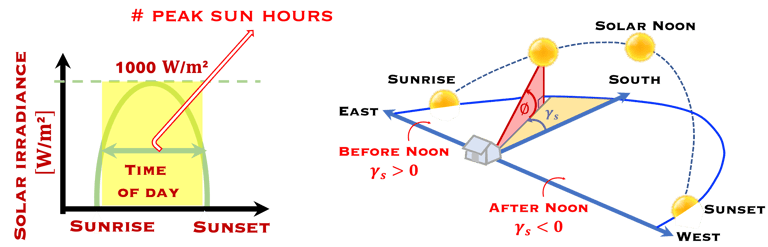
Avec les conditions STC (25°C, AM1.5, 1 kW/m²) et en supposant l´insolation (1 kW/m²) constante, nous intégrons la période d'insolation maximale de 10 heures -pour obtenir les heures d'ensoleillement maximal quotidiennes en unités [kWh/m²]: e.g. [kW/m² ] × 10 heures = 𝟏𝟎 kWh/m²
Considérons maintenant une surface de toit de 40 m² disponible, et supposons que le propriétaire a acheter des modules ayant un rendement de EFF = 15% chacun. Quelle est la puissance nominale des modules sur le toit ?
1 kW/m² de rayonnement est le pic (Wp) moyen d'ensoleillement reçu à la surface de la Terre (par exemple, en une journée d'été avec un ciel dégagé)
La puissance nominale PSTC d'un module en Watt-Peak [Wp ] décrit la puissance de pointe du module sous STC
Le rendement de conversion nominal est définie comme suit:

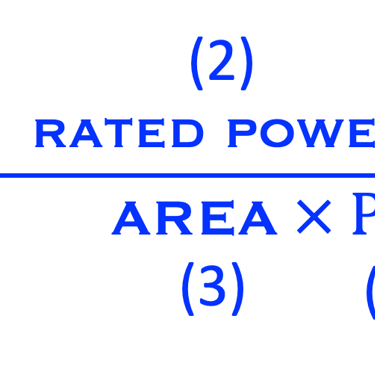


(1) Rendement de conversion
(2) Puissance nominale"
(3) Surface des panneaux
(4) Conditions standards (STC)
Il faut garder à l'esprit que la production d'électricité générée par le système photovoltaïque dépend de plusieurs facteurs tels que :
Rendement des modules PV
Efficacité de l'onduleur (conversion du courant continu délivré par les panneaux PV en courant alternatif
Rayonnement solaire réel
Dégradation des cellules solaires du module PV
Température des modules
Salissure (particules de poussière sur les surfaces du panneau)
La réponse : PSTC =1 kW/m² x 40 kW/m² . 0.15 = 6kWp
Nous supposons une formule générale, ci-dessous pour obtenir la production annuelle d'énergie (Eannuelle ) d'un système PV est donnée par (*)

E = Energie produite annuellement [kWh]
A = Surface de chaque panneau solaire PV [m2]
EFF. = Rendement du panneau solaire [%]
STI = Rayonnement solaire moyen annuel sur les panneaux inclinés
PR = Facteur de performance, coefficient pour toutes les pertes
Nous considérons des panneaux PV d'une surface S = 1.64 × 0.99=1.6236 m² et chaque panneau délivre une puissance de crête de PSTC = 240 Wp
Calculons le rendement d'un module avec une telle puissance
PSTC = 240 Wp = 0.240 kWp
EFF. =240Wc /(1000×1.6236) = 14.78 %
Nous divisons cette discussion en plusieurs étapes:
Nous calculons la consommation électrique totale
Prenons un exemple : les appareils (e.g. Une lampe fluorescente de 18W pour 4H/jour, Un ventilateur de 60 W pour 2H/jour, 75 W Réfrigérateur fonctionnant 24 H avec un compresseur fonctionnant pendant 12 H, et 12H à l´arrêt)
Nous calculons la quantité de watt-heures qui doivent être fournis aux appareils, en additionnons l´ensemble des watt-heures pour obtenir le total des wattheures par jour
(18W × 4H) + (60W × 2H) + (75W × 24H×0.5) =1092 Wh/day = 1.092 kWh/day
Il y a toujours de l'énergie perdue dans le système que nous compensons en multipliant le total des "Watt-heures" ( i.e 𝟏.𝟎𝟗𝟐 kWh/day ) par un coefficient (facteur d'économie de l´ordre de 1.3(**)
(**) Ce facteur d'économie permet de s´assurer que le nombre de modules achetés fournira assez d'énergie (mieux vaut plusd´énergie que moins)
L´énergie totale délivré par les panneaux est de:
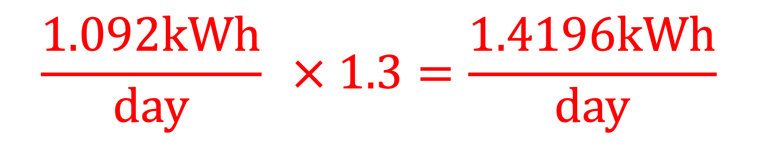
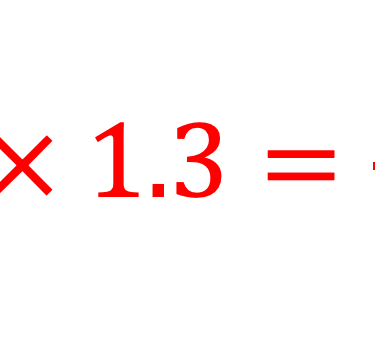


Nous introduisons un autre facteur appelé "le facteur de génération du panneau" "Panel Generation Factor, ou PGF(***)
(***) PGF = 3.43 for Thailand, and 2.93 in EU countries after wikipedia / PGF: https://en.wikipedia.org/wiki/Panel_generation_factor
La puissance totale en watts-crête ou Wc-T de la capacité PV nécessaire par jour peut être obtenue comme suit
Supposons que l'on choisissent des modules PV ayant chacun une puissance nominale PSTC = 250Wp, cela signifie que chaque module PV peut fournir par heure un maximum de 250Wp (i.e. 250Wh). Le nombre de modules
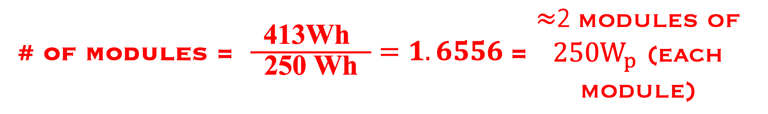
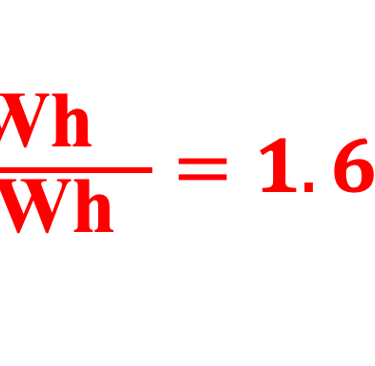
Dans ce calcul, vous devez toujours augmenter la partie fractionnaire du résultat jusqu'au nombre entier le plus élevé, ce qui correspond au nombre minimum de panneaux PV requis (ici 1,6556 est arrondi à 2 modules).
L'utilisation de modules de 110Wp nous donne:
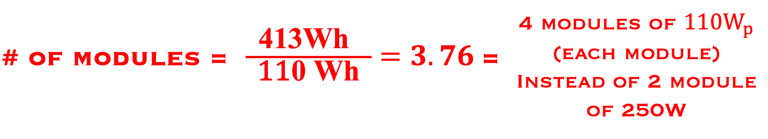
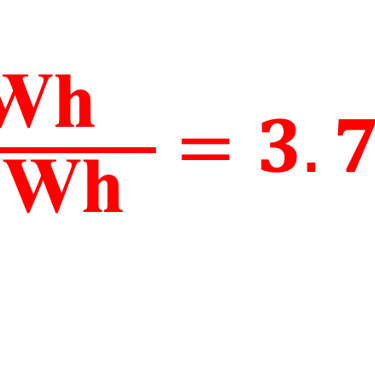
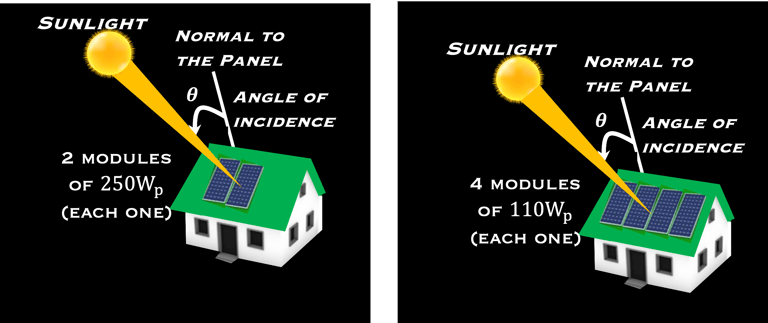

Nous avons déterminé la quantité d'énergie en 𝑘𝑊h/jour consommée par la charge, et le nombre de panneaux solaires dont nous avons besoin en tenant compte des pertes, pourtant il faut garder à l'esprit qu’il y a d'autres pramètres à prendre à considérer pour obtenir ces résultats plus de avec précision. Ces questions seront traitées dans les cours de l´équilibre
des systèmes où d'autres éléments entrent en jeu telles que les onduleurs, les régulateur de charge, Les batteries,
Le cablage, etc… doivent être pris en considération.
Pour tout projet de transition énergétique, la précision de la mesure de la ressource solaire et les conditions climatiques du site jouent un rôle crucial. Ceci permettra aux décideurs politiques de prendre de meilleures décisions pour que l'électricité produite à partir de l'énergie solaire augmente dans des projects moins coûteux et fiables
Le cours que nous proposons aux étudiants des universités et écoles d'ingénieurs marocaines, ainsi qu'aux chercheurs dans le domaine de l'eau et de l'énergie est une approche multidisciplinaire et durable pour la production d'eau dessalée, d'hydrogène vert et d'énergie électrique
Nous nous concentrons sur au moins cinq piliers
Salissures and solution
Données solaires et réseau intelligent assisté par l'IA
Développement de dispositifs solaires efficaces pour la production de l’hydrogène vert avec l'électricité solaire et l’eau de mer
Projet pilote (par exemple, la ville marocaine de Laayoune)
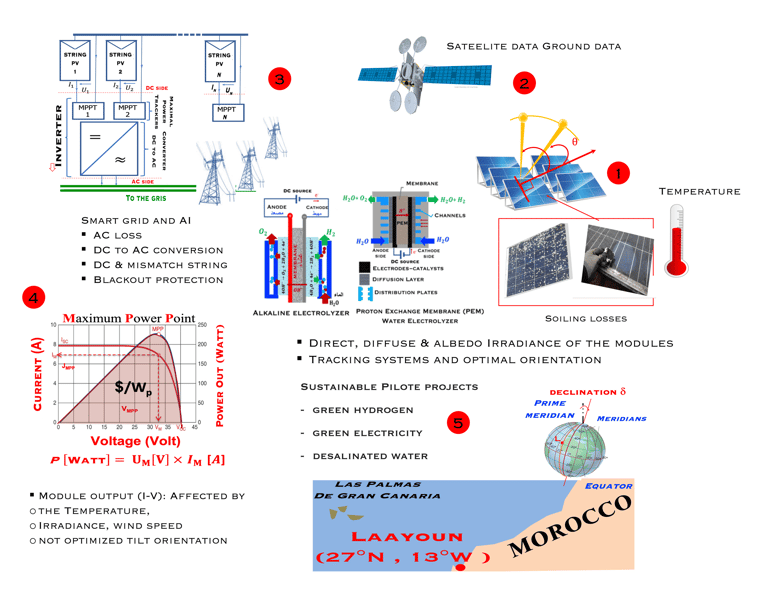
Projet: Performance, modélisation et simulation de production d’hydrogène vert par dissociation l’eau désaliénée : L'hydrogène décarboné est une des solutions d'un point de vue environnemental, pour répondre à la décarbonation de l’industrie et des transports. Le Maroc est engagé pour réduire sa dépendance aux énergies fossiles importées et l'hydrogène vert permettra au Maroc d'assoir son indépendance en maîtrisant les technologies renouvelables. Alors, ce projet consiste à modéliser et simuler la production de l'hydrogène par électrolyse de l’eau désaliénée qui se décompose en hydrogène et en oxygène au moyen d’un courant électrique continu produit par des modules photovoltaïques, l’alimentation en eau s'effectue par une centrale de desalination de l'eau de mer qui utilise aussi l'énergie photovoltaïque pour assurer la desalination de l'eau par osmose inverse. Les électrolyseurs alcalins, et à membrane seront choisies dans ce travail (voir le cours en anglais sur l'hydrogène vert). Le choix de la ville de Laayoune est trés stratégique géographiquement et est située au bord de la Mer. Il faut envisager les différents challenges (I) les infrastructures de desalination de l'eau. (II) les infrastructures de production de stockage et distribution d’hydrogène. (3) les problèmes liés à l´installation photovoltaïque indiqués dans l'illustration tels que (1) l´orientation optimale du système PV, le nettoyage des panneaux, le problème de la température. (2) comment exploser les données satelitaires, (3) le couplage avec le réseau pour injecter le surplus, (4) le chois des technologies PV pour obtenir le maximum d'électricité verte. Étude du cas précis de Laayoune et choix de technologie de stockage pour découpler la demande et la production d’énergie (ce projet sera discuter tout au long de ce cours)
Dans ce qui suit nous exploitons tous les paramètres géométriques relative du soleil par rapport à un observateur au sol, tels que: la latitude en degré, l´azimut solaire, la déclinaison du Soleil, δ, Angle horaire, ω, le diagramme solaire
Un premier conseil pour obtenir une production maximale de vos installation PV "e.g. Roof top" tout au long de l'année, vous devez au moins incliner les panneaux en fonction de la latitude de votre maison
La terre tourne sur son axe, et nous avons le jour et la nuit
La terre tourne autour du soleil sur l´orbite elliptique en 365 jours 1/4
L'axe de rotation de la Terre est incliné par rapport à son plan orbital, c'est l'origine les saisons
Le terme équinoxe signifie l'égalité du jour et de la nuit
Il a lieu le 21 mars et le 21 septembre
Une ligne reliant le centre du Soleil au centre de la Terre passe par l'équateur
partout sur Terre, le jour et la nuit durent 12 heures chacune
Ceci correspond à la période du printemps et de l'automne
Le 21 juin, le pôle Nord est plus proche du Soleil
Les journées sont plus longues dans l'hémisphère nord
Plus courtes dans l'hémisphère sud
C'est le solstice d'été dans l'hémisphère nord et le solstice d'hiver dans l'hémisphère sud
On December 21, the tilt of Earth’s spin axis makes the South Pole closer to the Sun than the North Pole,
Les journées sont plus courtes dans l'hémisphère nord
Plus longues dans l'hémisphère sud
C'est le solstice d'hiver dans l'hémisphère nord et au solstice d'été dans l'hémisphère sud
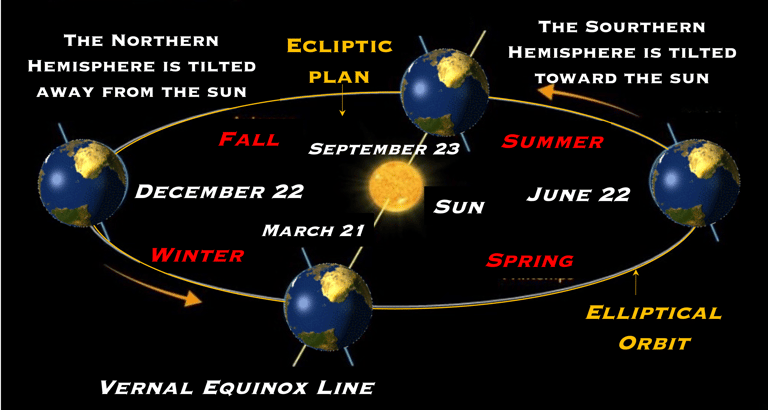
Le soleil, la terre et l'intermittence de l'énergie
Ce qu'il faut savoir sur une location donnée, Cas: Coordonnées GPS géographiques de Laayoun
Latitude : 27°08′30″ N (ou décimal 27.1418000°)
Longitude : 13°11′16″ W (ou décimal -13.1879700°)
Altitude de la position géographique : (68 m au-dessus du niveau de la mer)
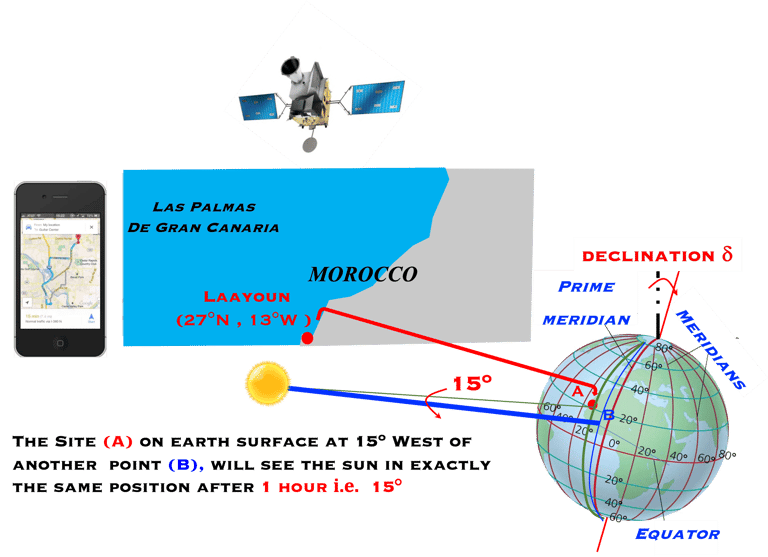
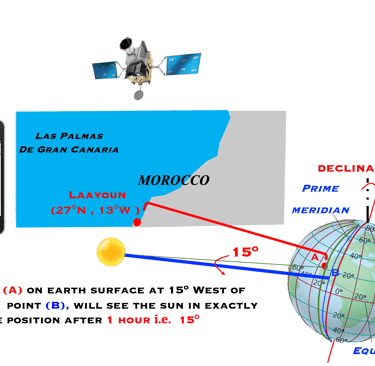
La longitude mesure le nombre de degrés à l'est ou à l'ouest du méridien d'origine, entre -180° et +180°
1 jour = 24 heures, et la terre tourne 360° pendant cette période, i.e. la terre tourne de 15° toutes les heures (1h = 15° de longitude)
Toutes les lignes longitudinales de 360° passent par les pôles
Les lignes de latitude indiquent le nombre de degrés au nord ou au sud de l'équateur
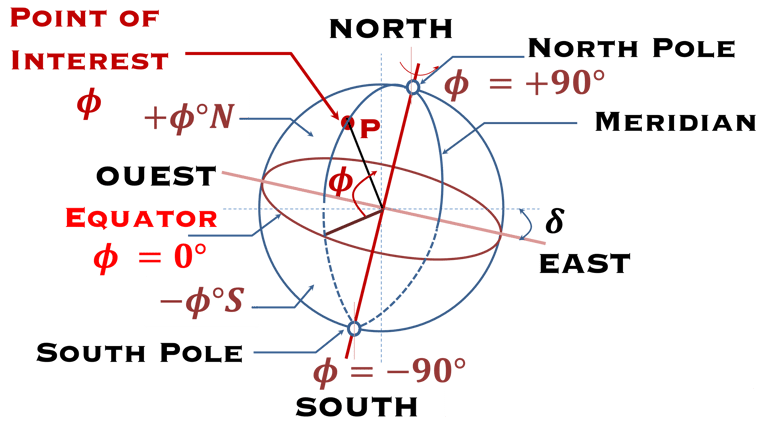
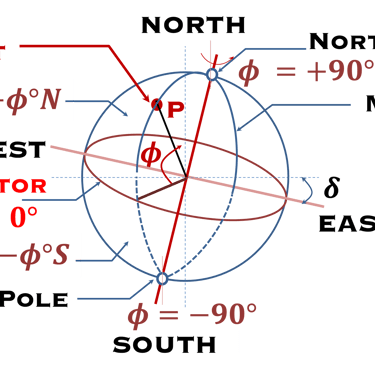
Le « méridien d'origine » passe par l'observatoire de Greenwich à Londres
La ligne longitudinale zéro passe par Greenwich
Les positions situées à l'est du méridien d'origine ont une adresse de longitude est (E)
Les positions situées à l'ouest du méridien d'origine ont une adresse de longitude ouest (W).
Variables solaires pour prédire la trajectoire du soleil
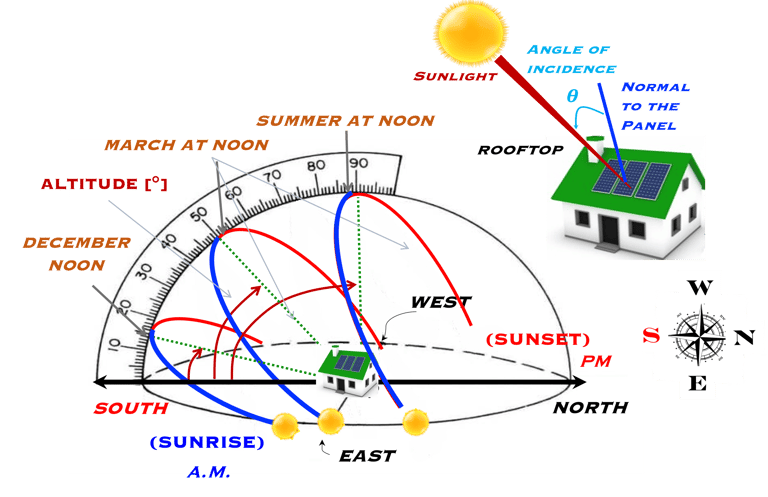
On en conclut que l’inclinaison optimale pour les panneaux solaires n’est pas la même en fonction des saisons.
L'orientation sud doit être favoriser dans tous les cas, car elle permet une exposition prolongé au soleil.
L'inclinaison des panneaux devrait être égale à la latitude géographique de la location
La latitude indique votre position sur l’axe entre le pôle Nord et le pôle Sud
Un panneau placé à l’horizontale a une inclinaison de 0°
Un panneau placé à la verticale, son inclinaison est de 90°
L´utilisation d'un suiveur solaire (Tracker en anglais), permet à un panneau solaire de se mettre dans la bonne inclinaison face aux rayons du soleil
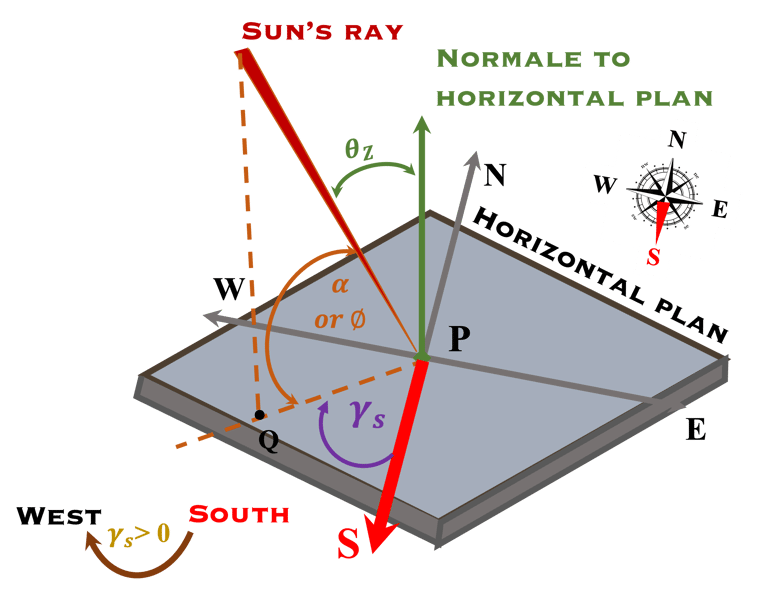
Angle zénithal θZ entre le rayon du soleil et la normale au plan horizontal
θZ = complément de (altitude) α
θZ + α = 90°
θZ = + 90° (lever du soleil)
θZ = -90° (coucher du soleil)
Inclinaison α entre le rayon du Soleil et la projection sur PQ
Lever et coucher du soleil ∅ = 0°.
Azimut solaire γs
γs est considéré comme positif du Sud vers l'Ouest
Nous mesurons γs par rapport à la direction du sud
Plan incliné avec Angle d'inclinaison β
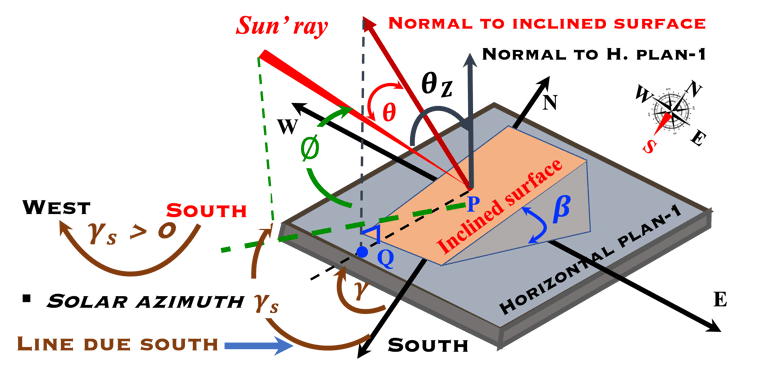
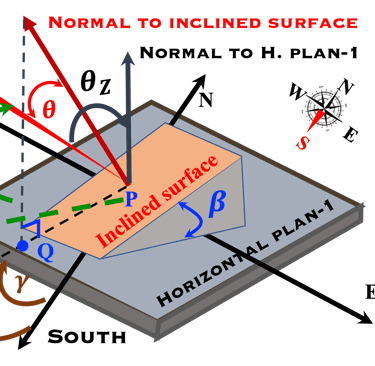
Plan incliné avec Angle d'inclinaison β = Angle entre la surface inclinée et le plan horizontal
Angle d'incidence θ = Angle entre le rayon solaire incident sur la surface inclinée du plan et la normale à cette surface
Pour une surface horizontale ( β = 0° ) et un angle zénithal θZ = θ
inclination ∅
« Azimut de la surface 𝜸 = Angle dans le plan horizontal entre la ligne plein sud et la projection horizontale de la normale à la surface du plan incliné
γ est considéré comme > 0 lorsqu'il est mesuré du sud vers l'ouest
Plan horizontal
Nous avons représenté les trois cas de figures les plus important
L´hiver (Décembre) , où le soleil se lève au sud-est et se couche au sud-ouest
L'équinoxe (Mars), où le soleil se lève à l'est et se couche à l'ouest
L´été, où le soleil se lève au nord-est et se couche au nord-ouest
En été, la courbe du soleil passe plus haut dans le ciel ;
En hiver, elle passe plus bas.
QUIZ: N-B- Les équinoxes sont le seul moment où l'hémisphère nord et l'hémisphère sud connaissent des périodes de jour et de nuit à peu près égales. Sur Terre, il y a deux équinoxes par an : l'un autour du 21 Mars et l'autre autour du 22 Septembre. L'équinoxe de mars est l'équinoxe de printemps dans l'hémisphère nord et l'équinoxe d'automne dans l'hémisphère sud. L'équinoxe de septembre est l'équinoxe d'automne dans l'hémisphère nord et l'équinoxe vernal dans l'hémisphère sud.
On vous demande de calculez la densité de puissance du soleil éclairant une cellule solaire plate sur le sol, le 22 septembre 2012 (équinoxe d'automne, lorsque le centre du soleil et l'équateur de la terre sont dans le même plan à midi). Nous supposons que le rayonnement solaire soit constitué de rayons parallèles ayant une densité de puissance perpendiculaire aux rayons de 1.35kW/m² , nous négligeons les pertes dues aux effets atmosphériques.
INDICATION : Nous supposons que les contributions atmosphériques sont négligées, de sorte que tout ce qui nous intéresse est la densité de puissance effective sur la cellule due au rayonnement incident 𝑃0 = 1.35kW/m². Il faut tenir compte de l'angle d'incidence du soleil sur la cellule, qui est posée à plat sur le sol.
Nous aurons besoin de la latitude de Golden, on prendra celle de Laayoune (Latitude : 27°08′30″ N i.e. en décimal 27.14°). 1.35kW/m² cos 27.14 ≈ 1.215kW/m²
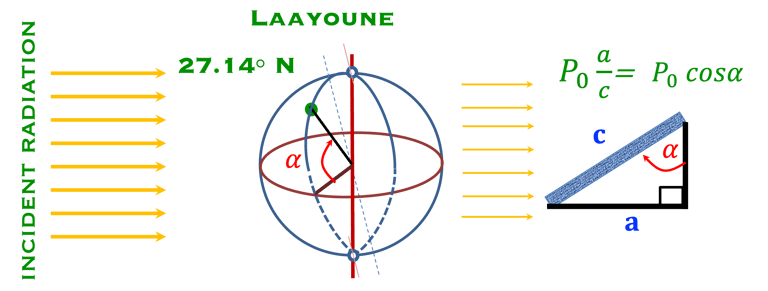
Angle horaire ω et angle d'élévation , h
Le nombre de degrés que la terre doit tourner avant que le soleil ne soit au-dessus de votre ligne de longitude est appelé angle horaire (HA ou ω):
ω = (15°)/h x [Heure avant midi]
Relation pour la conversion de l'heure solaire locale (LST)* en degrés : 𝝎 = 𝟏𝟓°[𝑳𝑺𝑻 -𝟏𝟐].
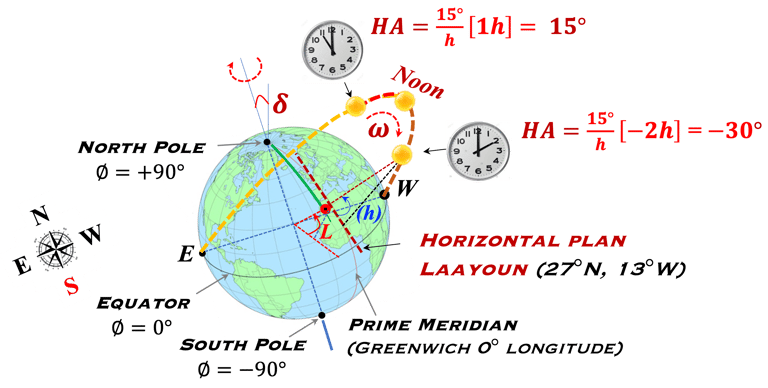
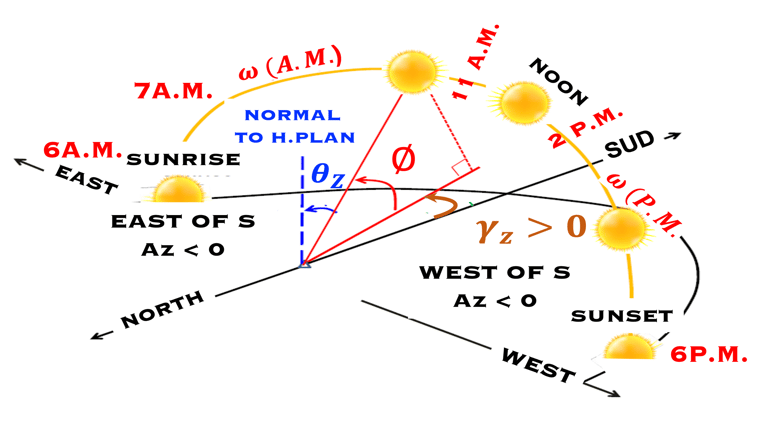
Trouver dans la figure, les réponses aux questions ?
Quel est l'angle d'altitude ∅ ?
Quel est l'angle d'azimut 𝛾𝑧 ?
Quelle est la hauteur du soleil ?
Quel est l'angle zénithal 𝜃𝑍 ?
Quel est le complément de hauteur solaire pour atteindre le zénith ?
A combien d'heures correspond un angle de 15° ?
Utilisez cette relation : 𝜔 = (15°)/h [Heure avant midi] pour calculer l'heure exacte en degrés pour 6A.M., 7A.M., 11A.M., 2P.M., 6P.M.
HA, Az, 𝜹 et 𝐡 » sont liés entre eux
Hauteur angulaire h, du soleil dans le ciel, mesurée à partir du plan horizontal
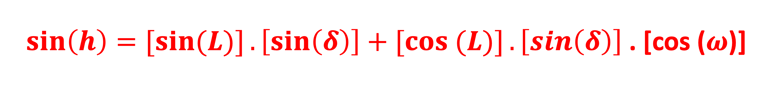
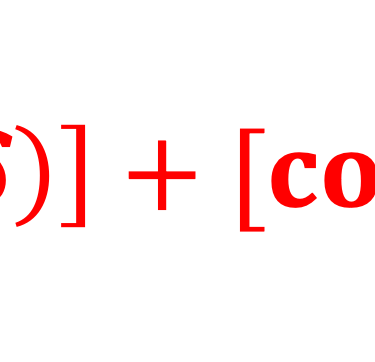
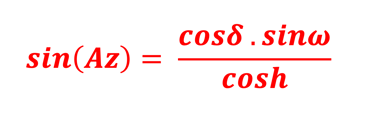
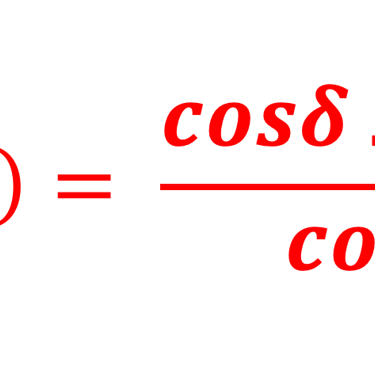
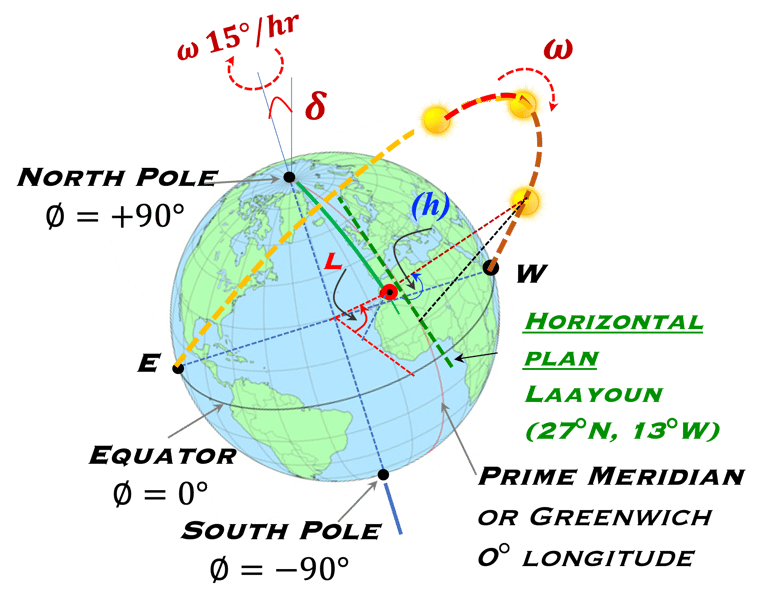
Angle azimutal (Az)
𝛿 = déclinaison
𝝎 = Angle horaire (HA)
L = latitude locale, définie comme l'angle entre une ligne allant du centre de la terre au site d'intérêt et le plan de l'équateur.
le centre de la terre au site d'intérêt et le plan de l'équateur
L'angle formé par l'axe terre/soleil et le plan de l'équateur) à un moment donné de l'année varie selon les saisons
𝛿 = 23,27°)au solstice d'été et d'hiver
𝛿 = 0 aux équinoxes
𝛿 prend toutes les valeurs intermédiaires
𝜹 s'exprime de différentes manières. Nous choisissons la formule :
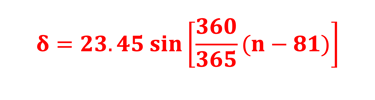
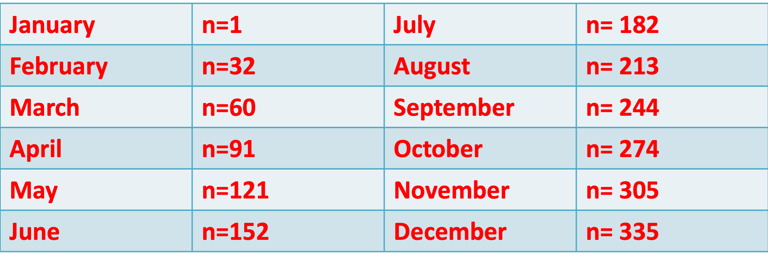
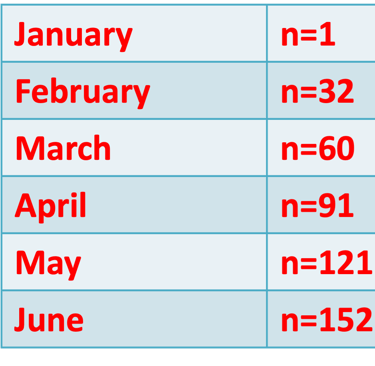
QUIZ to do: Trouvez l'angle d'inclinaison optimal d'un module photovoltaïque orienté vers le sud dans votre ville à midi solaire
(indication commencer par 𝛿 = déclinaison et identifier la Latitude de votre site )
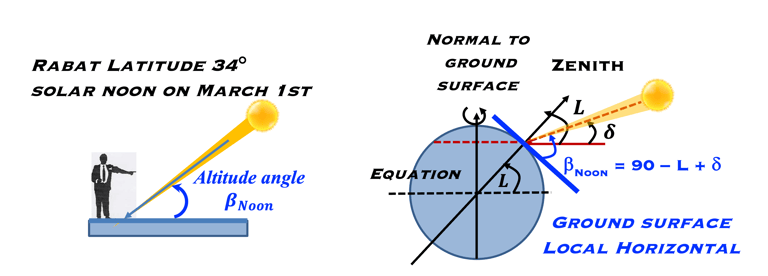
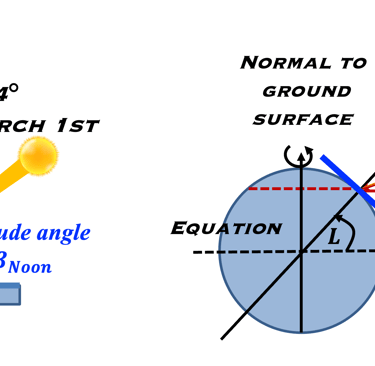
Premier Mars est le 60ème jour de l'année (n = 60)
L = 34° est la latitude du site

β à midi = 90° - L + δ = 90° - 34 - 8.3 = 47.7°
Tilt = 90 -β à midi = 90 – 47.7 = 42.3°
Le zénith présenté dans la figure se réfère à un axe tracé directement au-dessus de la tête
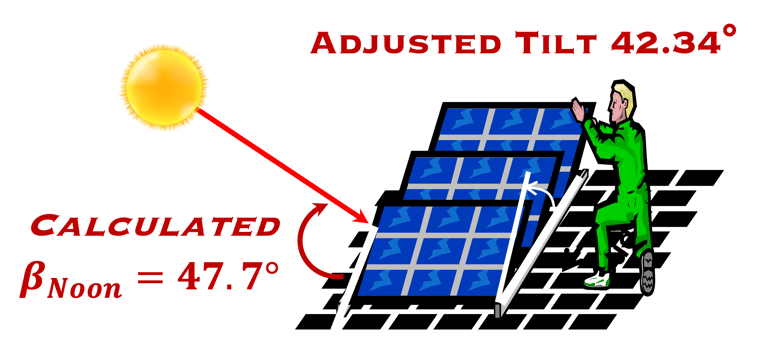

QUIZ: Trouver l'angle d'inclinaison optimal pour un module PV orienté vers le sud à Rabat (latitude 34° à midi le 1er mars).
Midi ou 12 heures de votre montre ne coïncide pas avec le midi solaire vrai (passage du soleil au zénith, c'est-à-dire le soleil au point le plus élevé dans le ciel)
Trois facteurs influencent ce petit décalage :
La longitude : la longitude (avec la latitude) décrit l'emplacement de votre point d'intérêt sur la terre
L'équation du temps
L'heure d'été
L’ÉQUATION DU TEMPS


Difference between a 24-h day and a solar day is given by the Equation of Time E


Lorsque l'heure d'été est en vigueur, une heure doit être ajoutée à l'heure de l'horloge locale
sources: World Time Zones: https://www.timeanddate.com/worldclock/


En combinant la correction de longitude et l'équation du temps, nous obtenons une relation finale entre l'heure locale (CT) et l'heure solaire (ST)
QUIZ: Trouvez l'heure d'été de l'Est pour le midi solaire à Boston (longitude 71,1° W) le 1er juillet.
Le 1er juillet est le jour n = 182. Pour tenir compte de l'heure locale, nous obtenons:


Pour Boston à la longitude (71,7° W) dans le fuseau horaire de l'Est avec le méridien d'heure locale 75°.
Nous ajoutons 1 heure, de sorte que le midi solaire sera à environ 12 h 48 (pour tenir compte de l'heure d'été).



Diagramme de la course du soleil
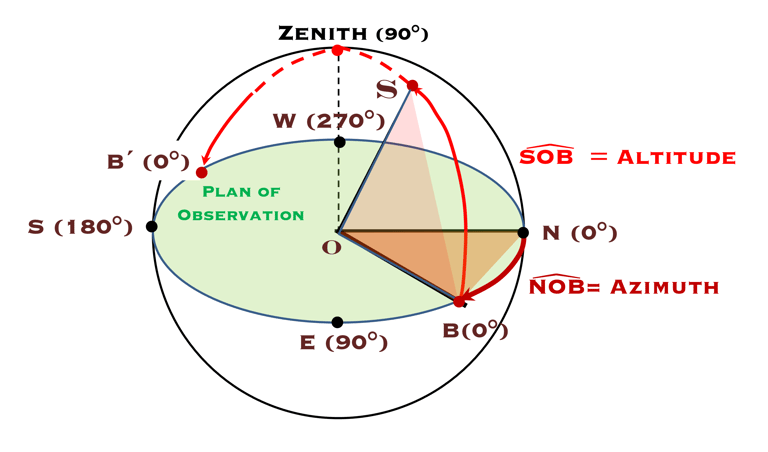
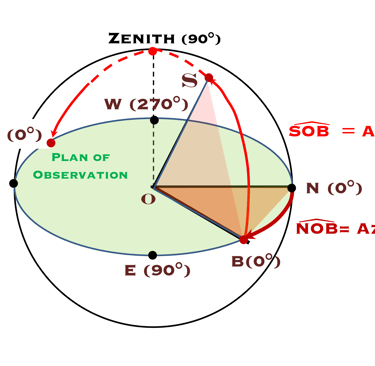
Comprendre la course du soleil pour établir facilement sa position à n'importe quelle moment de la journée est essentiel pour protéger l'environnement et économiser de l'énergie grâce à une conception passive des bâtiments par exemple. C'est un outil important pour les architectes et installateurs de panneaux solaires, et de constructeurs de tout système lié aux rayonnement et à l'efficacité énergétique.
Nous avons rappelé dans le diagramme (à gauche) certains éléments que nous avons étudié dans ce cours et que l´on trouve le diagramme de la course du soleil, tels que (horizon, zénith, hauteurs, azimuts)
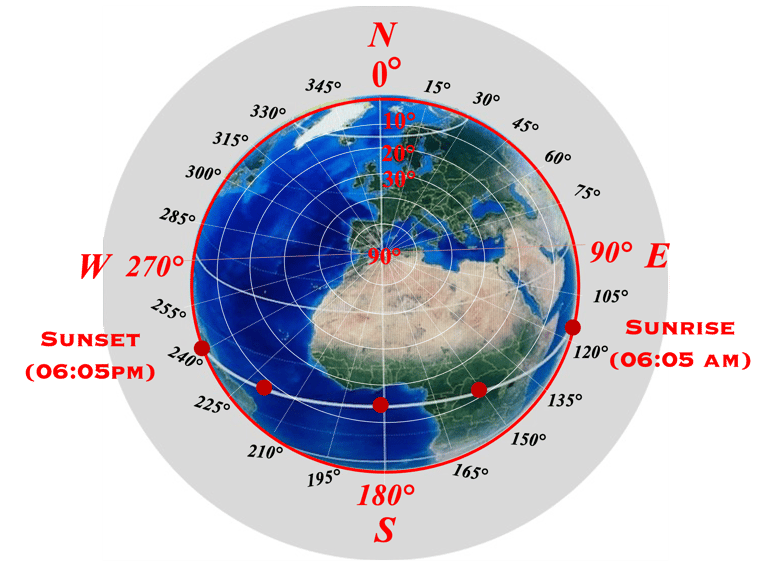
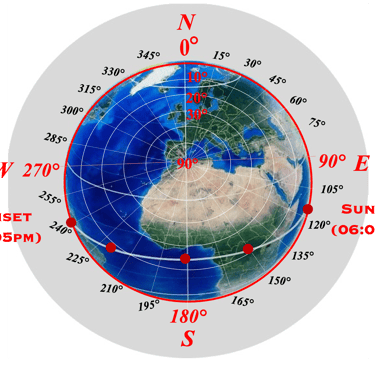
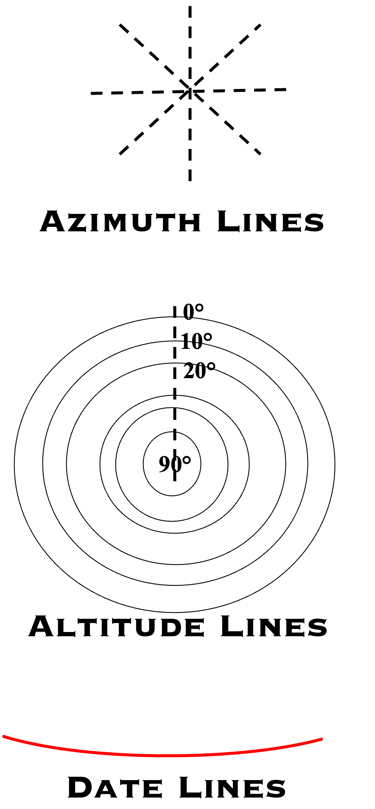
On peut se familiariser avec le diagramme de la course du soleil en identifiant les différents éléments tels que:
Les lignes azimutales
Les lignes d'altitude
Lignes des dates
On peut voir sur le diagramme de gauche les lignes azimutales
90° qui correspond à l´Est
180° qui correspond au Sud
270° qui correspond à l´Ouest
360° qui correspond au Nord
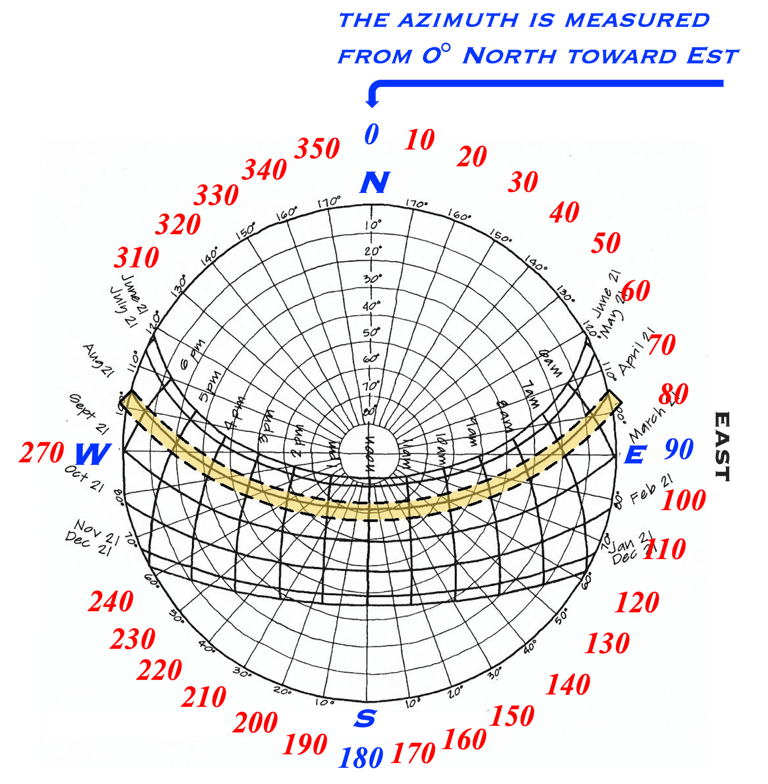
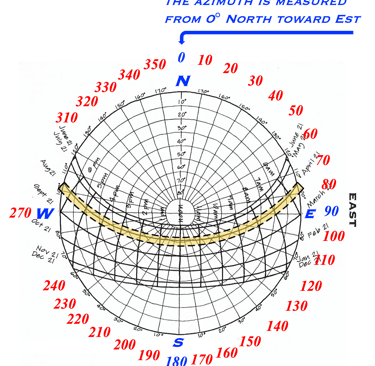
QUIZ: Quelle est l'altitude et l'azimut au 21 août. A 10 heures du matin ? Vérifier ce qui ne va pas dans la carte
Pour comprendre ce problème je vous propose de regarder la source (document) et regarder la video suivante:, ensuite explorer nots indications de solutions
source: utiliser ce document: https://hyperfinearchitecture.com/how-to-read-sun-path-diagrams/

Indication pour vous assister à résoudre le problème ci dessus
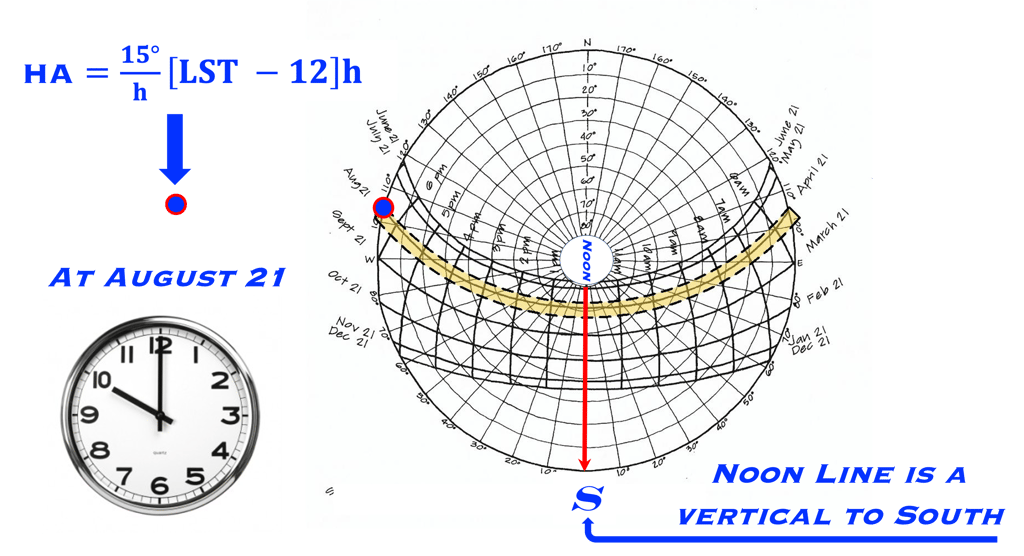
La conversion de HA (ou 𝜔 ) est HA = 15°/h[10-12]h = -30°
1er : Repérage du mois sur le diagramme 1
Ce sont les lignes pleines horizontales, mais légèrement incurvées
La ligne continue représente le 21 d'août. C'est la troisième en partant du centre
La flèche rouge indique verticale indique le sud (S)
Les lignes pleines et épaisses qui s'étendent verticalement, légèrement incurvées représentent le temps de la journée
La ligne indiquant midi (Noon) pointe directement vers le sud
Sur le diagramme à droite on va tout droit du cercle intérieur (Noon) au cercle extérieur à la valeur 60°
L'altitude est représentée par les cercles fins. Dans ce cas (diagramme 2) on est pas sur un cercle déjà tracé
Nous somme sur le cercle vert (L´intersection avec la ligne rouge légèrement incurvées donne l´altitude 50° < h < 60°)
L'azimut se lit sur le bord extérieur de la carte. Le nord est le 0 (origine), l'est le 90°, le sud le 180°, l'ouest le 270° et tous les 10 degrés intermédiaires
Tracer une ligne du centre au bord extérieur de la carte, en passant directement par la position du soleil marquée, alors on peut lire Az = 60°
Vous devriez dire Az = 60° à l'est du sud pour indiquer que vous utilisez le sud comme référence
Adapté du papier: document: https://hyperfinearchitecture.com/how-to-read-sun-path-diagrams/ (en anglais) que je vous conseil de lire ainsi de voir la video trés instructive
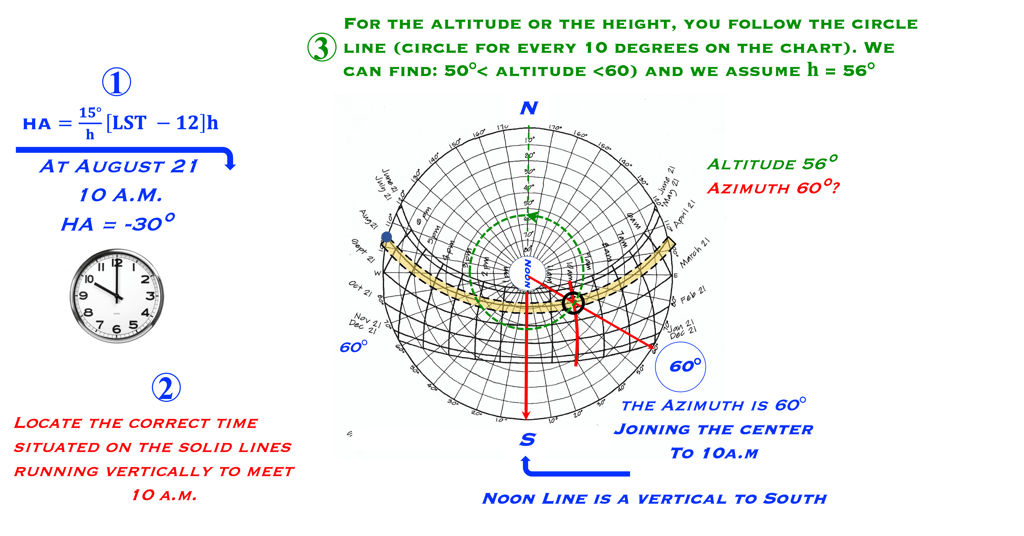
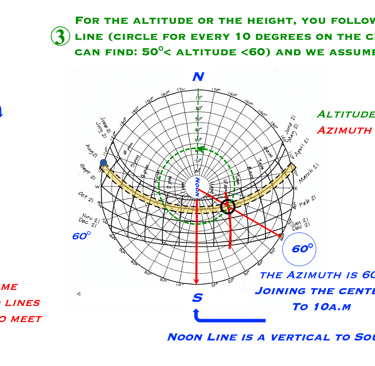
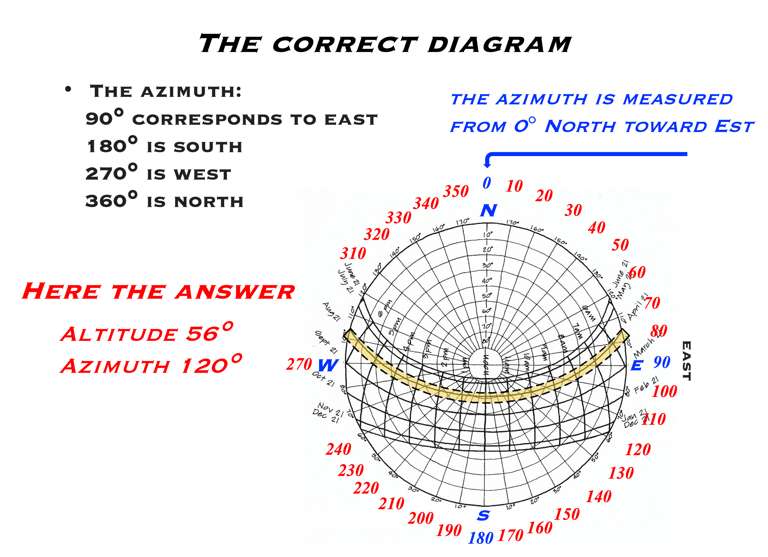
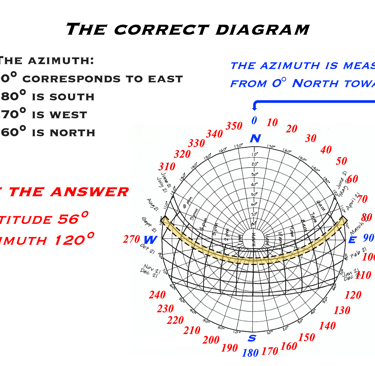
Les bases de la technologie des cellules solaire
Physique des cellules solaires photovoltaïque à base de silicium
Cette partie traite le passage des niveaux d'énergie aux bandes d'énergie, la notion de niveau de Fermi, de densité d'états dans les métaux et dans les solides semi-conducteurs, la bande de valence et de conduction et la notion et densité d'états (DOS) des électrons et des trous, l'équation de continuité et l'équation du courant de la diode. Principes de fonctionnement des cellules solaires : absorption de la lumière, génération de porteurs de charge, effet photovoltaïque, semi-conducteurs en équilibre et hors équilibre, bande interdite, transitions directe et indirecte. Comprendre les cellules solaires à jonction p-n, réponse spectrale et efficacité de conversion quantique (EQE, IQE), le rendement de conversion de l'énergie lumineuse en électricité. Décrire les étapes de base des processus de fabrication des cellules solaires au silicium : Production de silicium de qualité solaire, silicium de qualité métallurgique (MG), silicium de qualité électronique (SG), lingot mono-cristallin par le procédé Czochralski, du lingot aux plaquettes de silicium, procédés de fabrication des plaquettes. Comprendre le dopage, et fabrication de cellules, interconnexions, revêtements antireflets, texturation de surface et techniques de passivation. Compréhension approfondie des cellules et des modules photovoltaïques, les techniques de mesures des courbes I-V, de la réponse spectrale, du rendement quantique (EQE, IQE) et des mesures du rendement de conversion.
Comme nous l'avons discuté tout à fait au début de ce cours, un atome est déterminé par 3 nombres quantiques n, l, m, et un électron est décrit par une fonction d'onde ψ(r ⃗,t) ou dans le formalisme de Dirac par le "Ket" I(n, l, m)>. Le produit scalaire : lψ(r ⃗,t)l² = <(n, l, m) I(n, l, m)> représente la probabilité de présence de l'électron dans l'espace. Lorsque les électrons de deux atomes se rapprochent, leurs fonctions d'onde électroniques se chevauchent et la fonction d'onde devient une combinaison linéaire des deux fonctions d'onde individuelles donnant lieu à des orbitales liantes (Bonding, orbitals / stables).
Lorsque le nombre d'atomes augmentent et c'est le cas d'un crystal comme le silicium par exemple, le nombre d'orbitales donne leu à un rapprochement des niveaux d'énergie, cee rapprochement des niveaux d´énergie devient indiscernable, créant un continuum de niveaux d'énergie, appelé bande d´énergie
L´équation de Schrödinger dans les problèmes à N corps est très difficile à résoudre exactement et on utilise des approximations qui ne fond pas l'objet de secours. Nous donnons ici les principales approximations utilisées en physique quantique (le lecteur qui s'y intéresse peut consulté les livres affichés en bas de cette introduction)
Les électrons du cœur appartiennent à des orbitales complètement remplies et sont localisés prés du noyau auquel ils appartiennent. On les associe donc aux noyaux pour former des ions qui occupent les nœuds du réseau cristallin
Les électrons de valence, qui appartiennent aux orbitales de valence non complètement remplies, sont les seuls électrons à considérer dans l’Hamiltonien
Approximation adiabatique ou de Born Oppenheimer : Cette approximation est basée sur l’idée de l’inertie des noyaux par rapport aux électrons au point qu’on peut considérer les noyaux fixes
Approximation du champ moyen : Dans cette approximation, on globalise les interactions en remplaçant toutes les interactions à deux corps par un potentiel moyen V(r) dans lequel baignent les particules
Approximation du champ moyen : Dans cette approximation, on globalise les interactions en remplaçant
toutes les interactions à deux corps par un potentiel moyen V(r) dans lequel baignent les particules
Méthode des liaisons fortes: Cette méthode, appelée aussi méthode LCAO (linear combinations of atomic orbitals),
consiste à développer la fonction d’onde du cristal sous forme de combinaisons linéaires d’orbitales atomiques en tenant compte du théorème de Bloch auquel doivent satisfaire les fonctions d’onde du cristal
Méthode des liaisons faibles : La méthode des liaisons faibles appelée aussi méthode OPW (orthogonalized plane waves) considère que, à l’opposée de la méthode LCAO, les états électroniques dans le cristal sont essentiellement les états de l’électron libre plus au moins perturbés par la périodicité du potentiel du cristal
Méthode du pseudo potentiel qui revient en fin de compte à un calcul de perturbation.
Méthode APW (augmented plane waves) qui nécessite des techniques numériques très sophistiqués et des machines puissantes pour effectuer les calculs lourds qui résultent de la complexité du formalisme utilisé
Tous ces méthodes ne seront pas développés ici nous allons nous contenter de donner des notions très simples pour aboutir aux outils que nous allons utiliser par la suite pour mieux comprendre la technologie des cellules solaires




Les niveaux d’énergie d'un atome isolé sont parfaitement déterminés par les nombres quantiques n, l, m.
Chaque niveau peut être occupé par seulement deux électrons de spins opposés, conformément au principe d’exclusion de Pauli
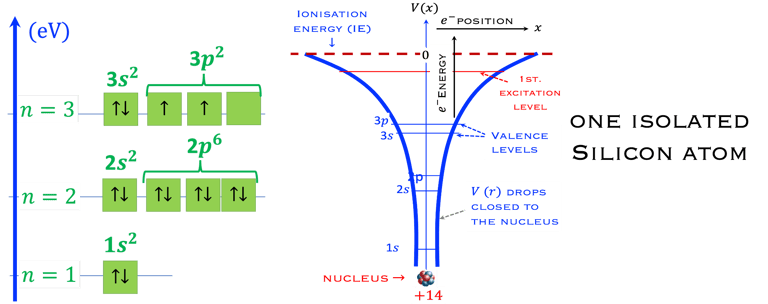
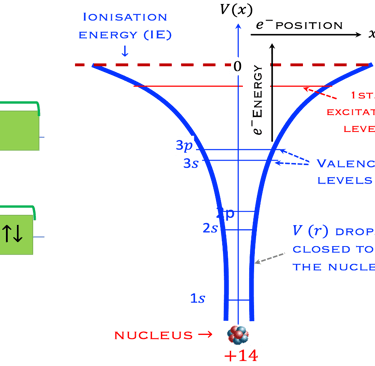
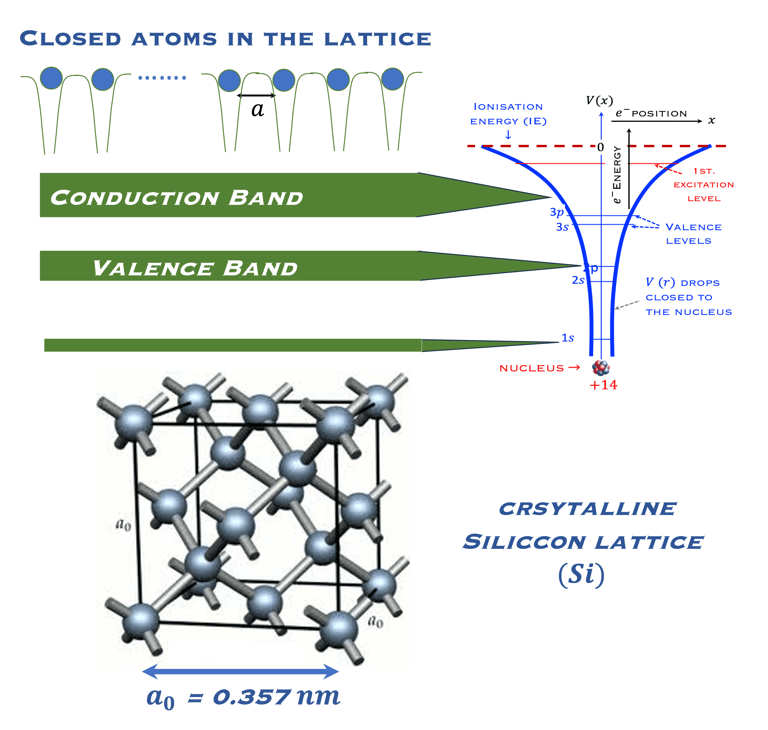
Nous passons d'un atome isolé à un solide cristallin où les atomes sont rassemblés dans un réseau cristallin
les états électroniques atomiques se séparent pour avoir des énergies différentes Les niveaux d'électrons sont regroupés en bandes de niveaux d'énergie
Les niveaux d'énergie sont étroitement espacés dans les matériaux cristallins
On peut obtenir des matériaux semi-conducteurs en partant du tableau périodique des éléments
La périodicité du réseau cristallin implique un potentiels périodiques qui permet d'obtenir un diagramme de bande d'énergie
Les électrons dans une structure périodique: le modèle de Bloch - Brillouin
On obtient des bandes d’énergie permise séparées par des bandes d’énergie interdites.
Deux bandes sont particulièrement importante pour la suite:
Bande de valence (BV): contient les états électroniques des couches périphériques des atomes du matériau (e.g. 4 electrons de valence pour le Si)
Bande de conduction (BC) : La bande permise immédiatement supérieure à la bande de valence
Dans la BC, les électrons sont quasi-libres, et permettent la conduction d’un courant sous l'action d'un champ électrique
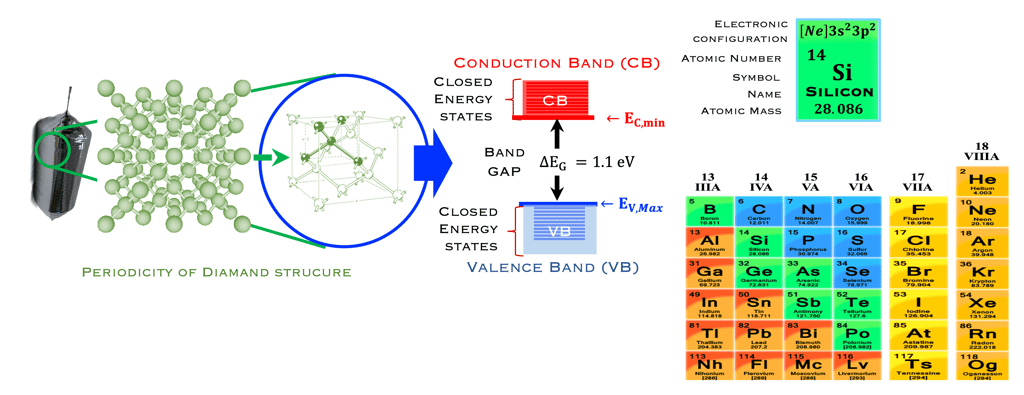
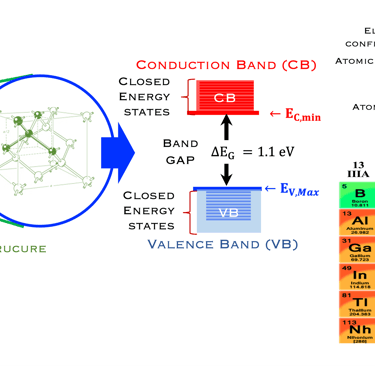
Considérons un cristal périodique de période a, (e.g. le silicium)
les propriétés du cristal sont les mêmes en x et x+a , x+2a , x+3a,...etc
La fonction d’onde, ψ(x) = ψ(x+a) = ψ(x+2a) = ψ(x+3a), ...etc
En mécanique quantique, le carré de l´amplitude de ψ est la probabilité de présence de l’électron dans un élément de volume dV
dP(x) = ψ*(x)ψ(x)dV = lψ(x)l²dV
dP(x+a) = ψ*(x+a)ψ(x+a)dV = lψ(x+a)l²dV
lψ(x)l² = lψ(x+a)l²
La fonction d’onde ψ(x) ne diffèrent de la fonction d'onde ψ(x+a) que par un facteur de phase: exp(i𝜃)
ψ(x+a) = ψ(x) exp(i𝜃) de même ψ(x+2a) = ψ(x) exp(i2𝜃) etc....
Généralement: ψ(x+Na) = ψ(x) exp(iN𝜃) = ψ(x)
Alors mathématiquement: exp(iN𝜃) = 1 i.e. 𝜃 = n.2π/N ou 𝜃 = n.2πa/Na
à ce niveau on va donner un sense physique à cette relation mathématique en introduisant le pseudo vecteur d’onde K = n.2π/L
Ceci permet d´ écrire: ψ(x+a) = exp(iKa).ψ(x)
K prend N valeurs consécutives distante entre eux de la quantité 2π/L (K est quantifié)
Modèle de Bloch Brillouin
Onde de Bloch
ψ(x+a) = exp(iKa) ψ(x) = expiK(a+x) . exp-iKx ψ(x) = expiK(a+x) [ψ(x). exp-iKx]
Posons u(x) = [ψ(x) exp-iKx] i.e ψ(x) = u(x) exp+iKx
mais u(x) = ψ(x) exp-iKx = ψ(x) exp-iK(x+a). exp +iKa = exp-iK(x+a) . ψ(x) exp +iKa = exp-iK(x+a) ψ(x+a) = u(x+a)
on en conclut u(x) = u(x+a) ou les fonctions d’onde stationnaire d’un électron dans un potentiel périodique sont des fonctions de Bloch de la forme
Onde plane et onde de Bloch
Onde plane = Aexp(ikx) avec k = 2π/λ
Onde de Bloch = u(x). exp-ikx avec k = n.2π/L
L’onde de Bloch est: u(x). exp ikx dans l’équation de Schrödinger
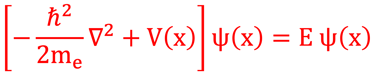
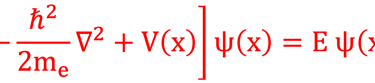
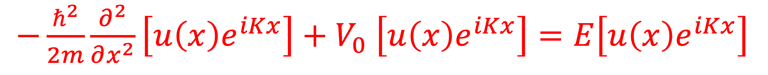
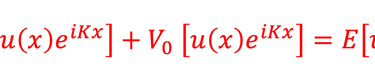
La résolution de l'équation de Schrodinger de Block impose une connaissance exacte la forme du potentiel cristallin V0
Une approximation consiste à utiliser un potentiel périodique qui traduit la périodicité du réseau cristallin, c'est le modèle de Kronig et Penney
Se référer à Wikipedia : https://fr.wikipedia.org/wiki/Particule_dans_un_réseau_à_une_dimension pour le détail de ce model
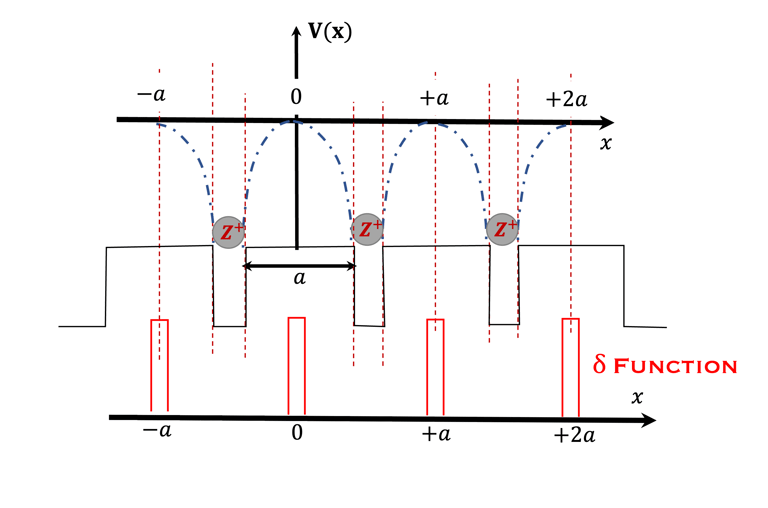
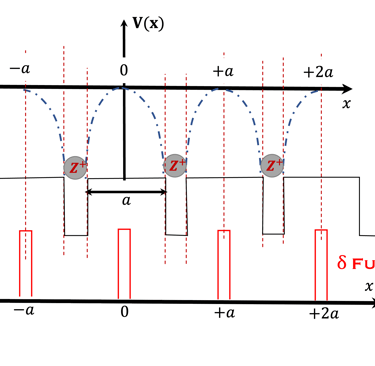
Un problème (Quiz) sera consacré à la résolution de l'équation de Schöodinger dans un potentiel périodique correspondant au modèle de Kronig et Penney
Nous présentons ici les résultats essentielles pour ce cours sur lles cellules solaires
À gauche: l'énergie d´une particule libre (V = 0)
À droite: l'énergie d´une particule dans un potentiel périodique V(x), et ayant la périodicité du réseau V(x) = V(x+Na) donnant lieu à une onde de Bloch
La figure du milieu illustre un potentiel périodique (idéalisé) représentant la périodicité d'un crystal par un potentiel périodique (idéalisé)
La particule qui se déplace dans ce potentiel périodique se trouve dans des bandes d’énergie séparées entre eux par des bandes interdite
Les états permis pour les électrons sont discrets séparés de Δk = 2π/a , il n’est pas nécessaire de tracer le diagramme sur tout le domaine de variation de k
La fonction d’onde est la même en x et x+a ainsi que la probabilité de présence de l’électron et par consequent les propriétés du cristal
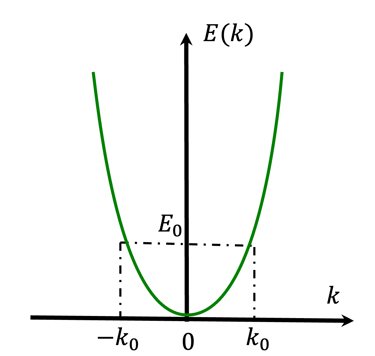
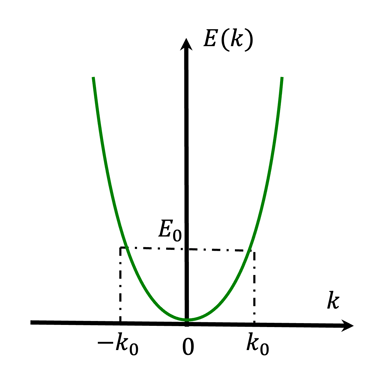
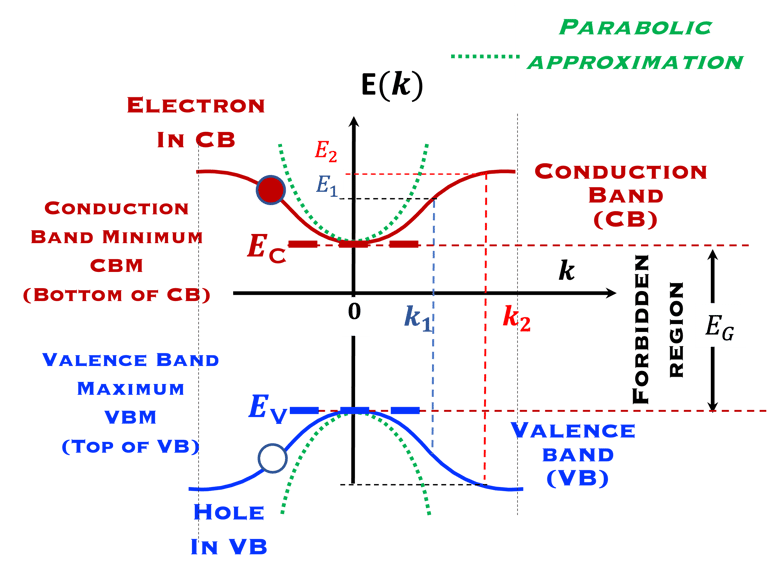
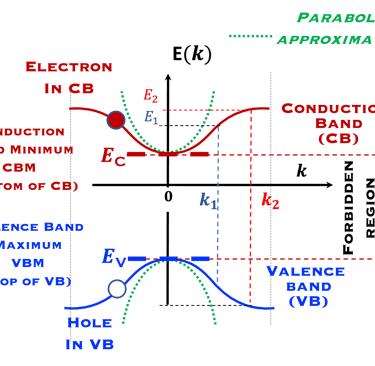
Modèle de Kronig-Penny, bande interdite et masse effective:
Deux résultats le important du modèle « KPM »
La forme du diagramme d'énergie E(𝒌) (à droite) qui décrit une particule dans un potentiel périodique V(x) = V(x+a) et qui met en évidence une région d'états d'énergie interdits (appelée aussi bande interdite ∆𝐸𝐺 ou 𝐸𝐺 )
La notion de masse de l'électron (valeur et signe) dépendant de la position de l'électron sur les bandes d'énergie, et est étroitement liée à la courbure des bande
Écrivons le développement limité de E(𝒌) jusqu'à l'ordre 2 au voisinage d’un extremum
On définit ainsi la notion de masse effective m* de l'électron
Nous avons illustré sur la figure ci-dessous, la masse effective de l'électron dans la band de conduction (Idem pour le trou dans la bande de valence)
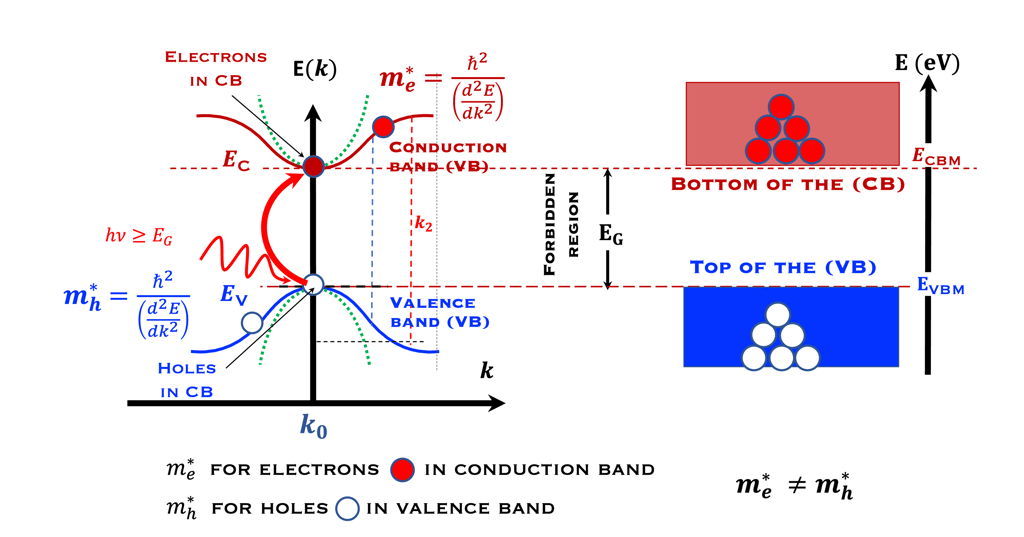
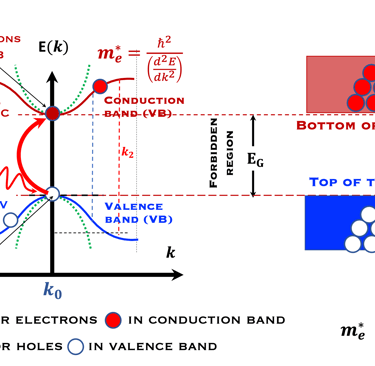
Ce concept assez simple est largement utilisé pour formuler la masse effective des électrons dans la bande de conduction et des trous dans la bade de valence
On peu voir ce phénomène comme lié au déplacement de l'électron dans un potentiel périodique qui modifie son inertie et donne ce concept de masse effective
Le problème est beaucoup plus complexe complexe à cause l´anisotropie due aux minima et maxima dans beaucoup de semi-conducteurs
Des changements au niveau de la masse effective sont attendus lorsque la relation de dispersion s'écarte de la forme parabolique
Nous comparons les structures des bandes du silicium et du GaAs deux semi-conducteurs d'une grande importance en microélectronique et en photovoltaïque
Pour l'arséniure de gallium (GaAs), le maximum de la bande de valence et le minimum de la bande de conduction se trouvent à une valeur adjacente du nombre d'ondes k dans le diagramme E(k), on a ici un semi-conducteur à gap direct (Eg, direct = 1,42 eV)
pour le silicium (Si), le maximum de la bande de valence et le minimum de la bande de conduction se trouvent à des valeurs distinctes du nombre d'ondes k dans le diagramme E(k), il s'agit donc d'un semi-conducteur à gap indirecte (Eg, indirect = 1,1 eV)
Source Sze "Sze, S. M. Semiconductor Devices: Physics and Technology, 2nd ed. New York: John Wiley and Sons, 2001
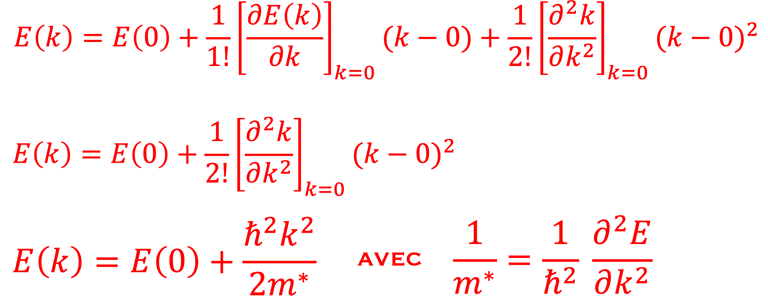
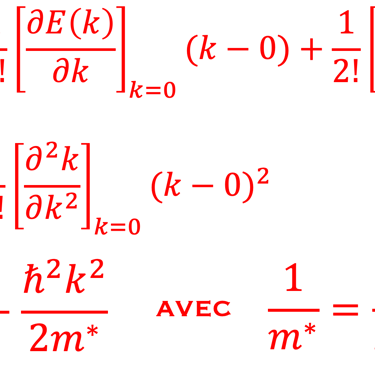
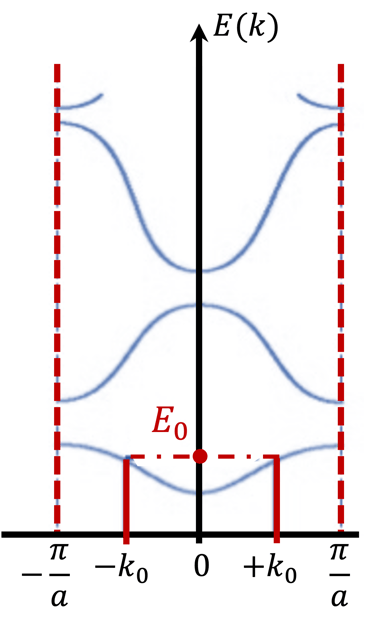
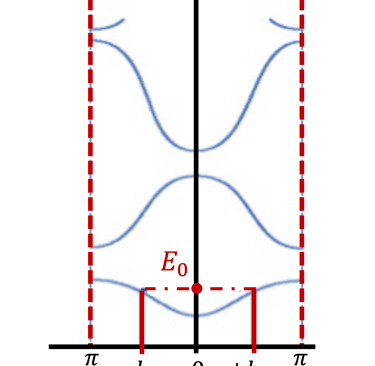

Class taught by Mark Lundstrom at Purdue University on Quantum Mechanics and Electron Waves in Crystal . This course help to understand (KPM)
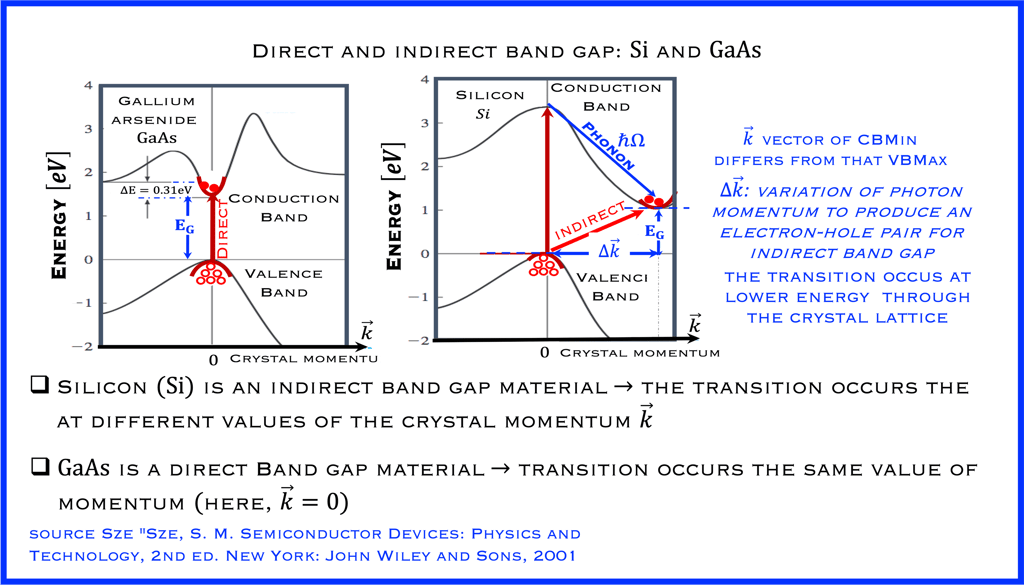
Avant de continuer regarder les videos de Mark Lundstrom at Purdue University sur le sujet


Densité d'état: Introduction
La densité d'état (DOS) désigne le nombre d'états électroniques par unité d'énergie pouvant être occupés par un électron dans un matériau.
Nous considérons que les électrons son presque libre dans leur mouvement au sein d'un matériau on va commencer par considérer l'électron complètement libres et son énergie se réduit à ε défini par
Par exemple, il y a un electron “libre” par maille, dans le cas d’un alcalin, i.e. pour N ions dans le cristal il y a aussi N électrons, à répartir sur des états
Le principe de Pauli impose 2 électrons par état, compte tenu du spin
On utilisera par la suite la notation E pour l'énergie E et va remplie les états dans une sphère représentée dans l'espace des cas par::


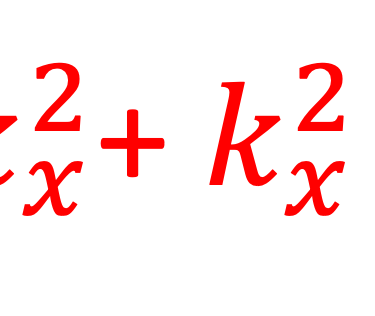
Densité d'état des électrons et des trous
Nous allons établir d'une manière simple l´expression analytique de la densité d'état (Dendity of surface State DOS) de l'électron sur une bande d´énergie
Le raisonnement que nous avons fait pour les photons est valable ici, sauf que les photons sont des Bosons et obéissent à la statistique de Bose-einstein alors que les électrons son des Fermions (de même les trous que Lyon considère comme absence d'électrons) obéissent à la statistique de Fermi-Dirac
L'expression de la distribution de Fermi-Dirac est représenté comme suit:
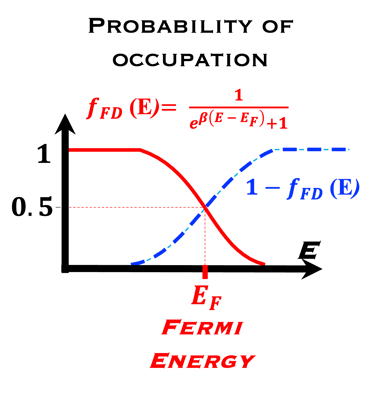
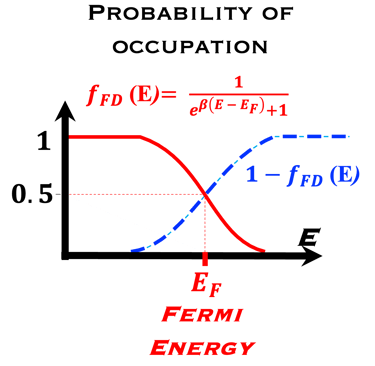
β = 1/kBT (k la constante de Boltzmann)
EF est le niveau de Fermi
EF = µ est aussi appelé le potentiel chimique,
EF = µ correspond à l’énergie pour laquelle la probabilité d’occupation pour un état à une température T donnée est égale à 1/2
La courbe rouge est la probabilité d'occupation des électrons
La courbe bleu est celle des trous
Nous calculé dans ce qui suit, la densité d'états D(E) des électrons D(E) qu'il faut multiplier par la probabilité d’occupation fF-D
De même, nous calculons la densité d'états des trous qui doit être multiplier par [1 - fF-D]


Nous allons compter le nombre d'état ou nombre de point dans la sphère représentée sur le schéma ci-dessous en remplissant des états dans dans l'espace des k (kx, ky, kz). Chaque petits cubes peut accepter deux ´electrons. Pour un alcalin, le nombre d’electrons “libres” est égal au nombre d’atomes, soit N


Nombre d'état ou nombre de point dans la sphère
Comme nous l'avons signalé au paravant, en raison de la dégénérescence du spin (2 électrons par état), le nombre d'électrons est donc toujours 2 x Nombre d'états (2 états de spin ∓1/2)
Nombre d'état de vecteur k dans la sphère
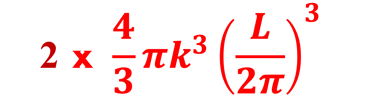
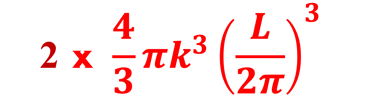
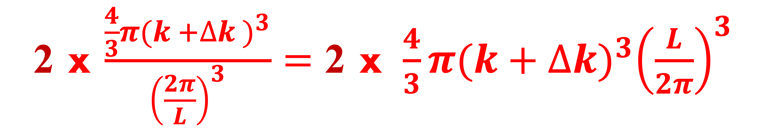
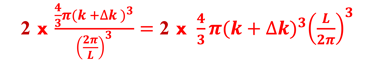
Nombre d'état de vecteur (k+Δk)
Établir la densité d'état D(E) à titre d'exercice (QUIZ)
Option-1: Faire la soustraction entre [Nombre d'état de vecteur k dans la sphère] et [Nombre d'état de vecteur (k+Δk)] et en déduire le nombre d'état dans un contour de largeur Δk (i.e. le nombre d'état dont le vecteur d'onde est compris entre k et k+Δk)
Option-2: Considérer ∆K<<1 (infinitésimal) ∆Np(K,T) tend vers dNp(K,T) et utiliser les propriété d´une "fonction continue f(x) et sa différentielle
df(x) = f´(x)dx où f´(x) c'est la dérivée i.e. la limite du taux d'accroissement [f(x+∆x)-f(x)]/∆x . Trouver le résultat suivant:
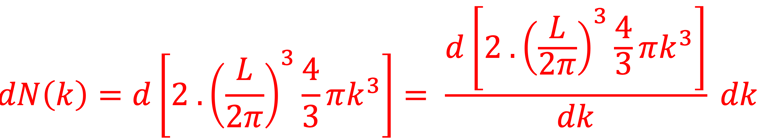
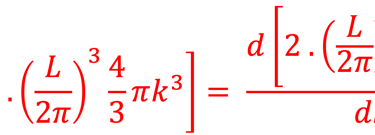
Effectuer la dérivée et trouver le nombre d'état dont le l'énergie est comprise entre E et E+dE, on utilisera les relations suivantes:
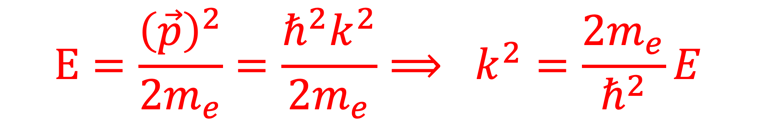
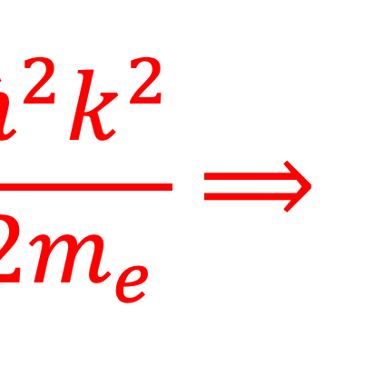
On trouvera une valeur de D(E) suivante
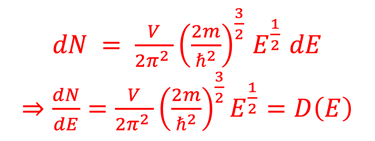
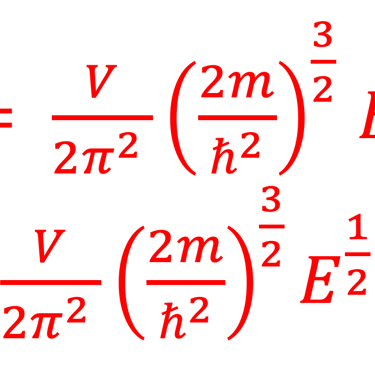
Le "niveau de Fermi" est le terme utilisé pour décrire le niveau d'énergie occupé le plus élevé à la température du zéro absolu
Les électrons sont des fermions, ils ne peuvent pas exister dans des états d'énergie identiques (selon le principe d'exclusion de Pauli). Aussi, le remplissage d'un électron sur un niveau d'énergie est modulé par la densité de Fermi-Dirac ou la probabilité d'occupation.
On peut imaginer placer 2 électrons en chaque point de l'espace des k, le nombre d'électrons est très grand et le résultat de ce remplissage ressemble beaucoup à une sphère (sphère de Fermi)
Le rayon de la sphère de Fermi est lié à l'énergie et au nombre d'électrons à la surface de la sphère de Fermi
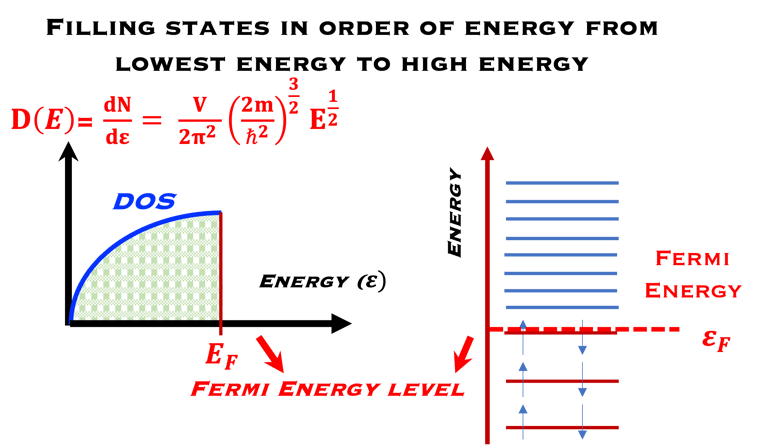
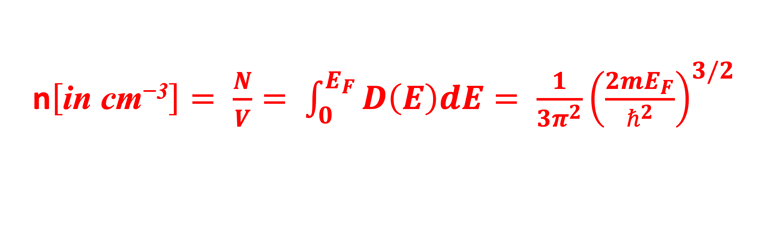
Imaginons que nous placions N électrons, qui remplissent les états par ordre d'énergie
Le dernier niveau d'énergie élevé rempli est par définition le niveau de Fermi (comme le montre la figure ci-dessos)
L'intégration de D(E) entre 0 et EF permet de trouver la relation entre le niveau de Fermi et le nombre N d'états
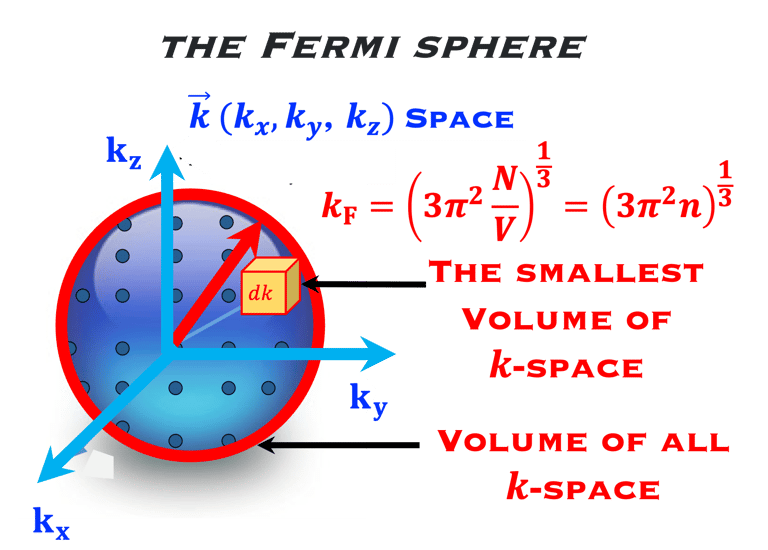
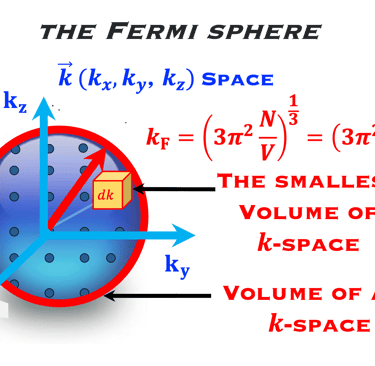
Le "niveau de Fermi" est le terme utilisé pour décrire le niveau d'énergie occupé le plus élevé à la température du zéro absolu
Les électrons sont des fermions, ils ne peuvent pas exister dans des états d'énergie identiques (selon le principe d'exclusion de Pauli). Aussi, le remplissage d'un électron sur un niveau d'énergie est modulé par la densité de Fermi-Dirac ou la probabilité d'occupation
La figure Ci-dessous montre la densité d'état D(E) (figure en √E à gauche) que Lyon a multiplié par fF-D pour trouver la densité d'état des électrons (Fermions)
Les niveaux d'énergie depuis le niveau le plus bas jusqu'au niveau de Fermi EF sont remplis pour T = 0K
La température implique que l'énergie cinétique des électrons augmente
Pour T voisine de la température ambiante 300K, alors kBT vaut environ 0.03 eV
Considérons l'orde de grandeur de l'énergie de Fermi d'environ 5 eV, i.e. kBT << EF
les états dans le voisinage de EF tel que |E−EF| ∼ kBT sont affectés
Les trois figures ci-dessous montre les états peuplés à T = 0 et T ≠ 0 qui influe la forme de la densité d'états autour de EF
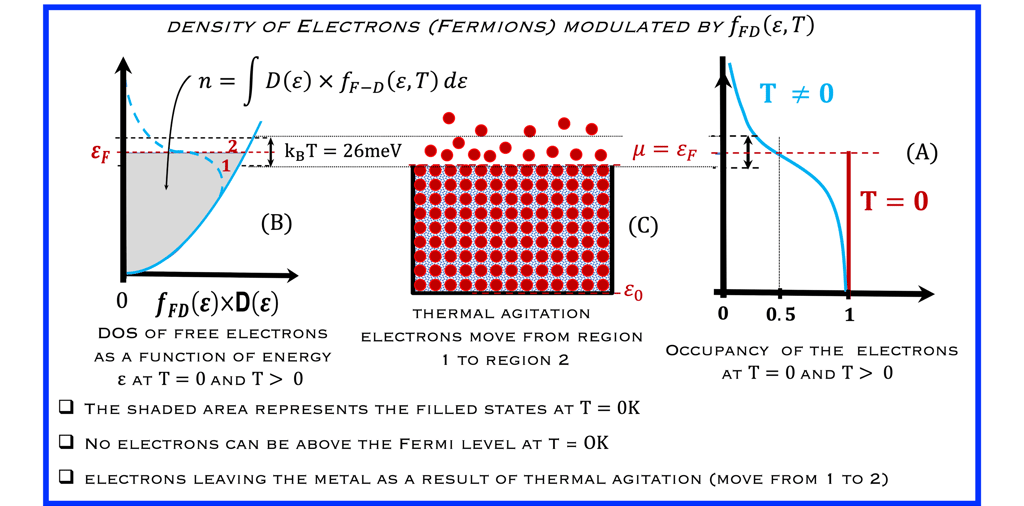
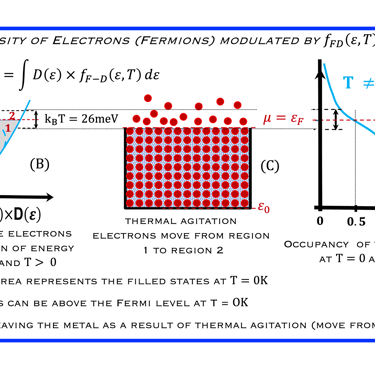


Densité D’états Dans Les Semi-Conducteurs
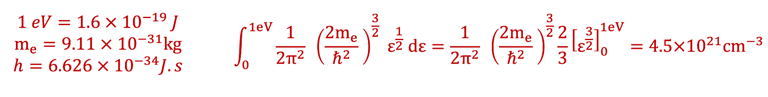
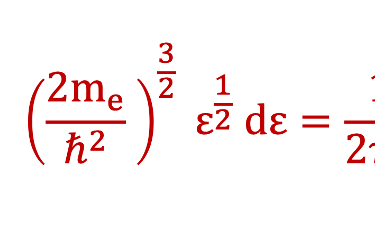
Densité d'états par unité de volume dans une gamme d'énergie donnée: calculez la densité d'états par unité de volume pour des énergies comprises entre 0 et 1 eV.
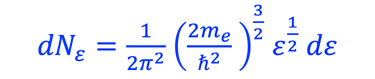
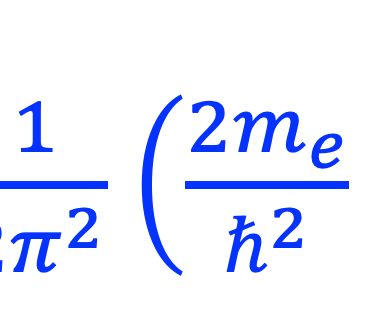
QUIZ: Le nombre 𝑑𝑁𝜀 , d'états par unité de volume dans l'intervalle [𝜀 , 𝜀+𝑑𝜀] est:
Regarder la video avant de continuer

Densité d'état DOS des électrons dans la bande de conduction
Pour formuler le nombre d'états d'énergie accessibles pour les électrons dans la bande de conduction par unité de volume et par unité d'énergie on doit tenir compte du faite que les énergies varient entre le bas de la bande de conduction et l´∞
Comme le montre la figure ci-dessous )à gauche), remplacer E par E -Ec dans la formule établie plus haut, il vient:
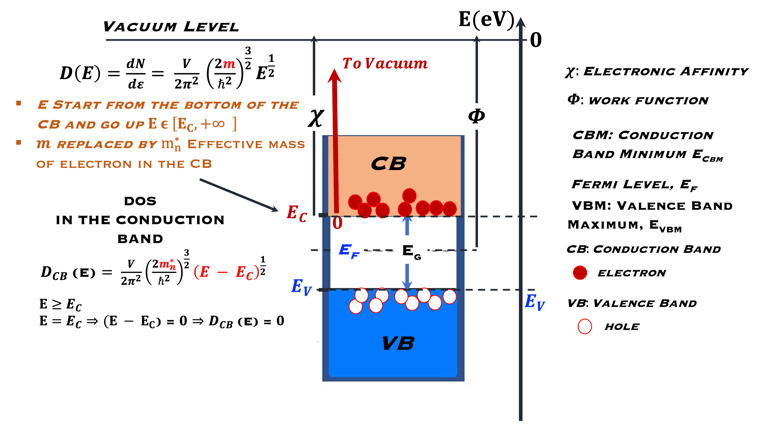
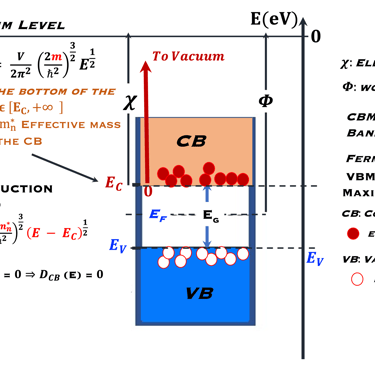
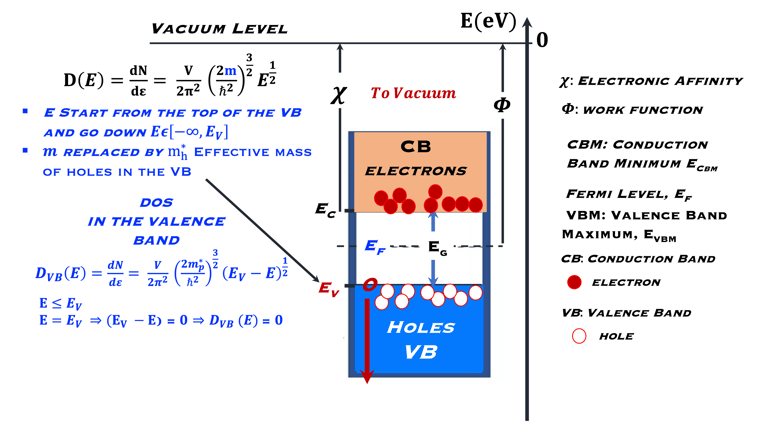
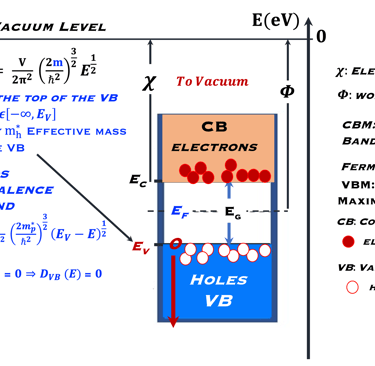
Densité d'état DOS des électrons dans la bande de Valence
Pour formuler le nombre d'états d'énergie accessibles pour les électrons dans la bande de valence par unité de volume et par unité d'énergie on doit tenir compte du faite que les énergies varient entre le haut de la bande de valence et - ∞
Comme le montre la figure ci-dessous (à droite), remplacer E par Ev -E dans la formule établie plus haut, il vient:
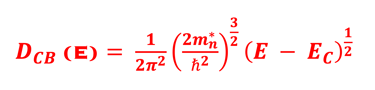
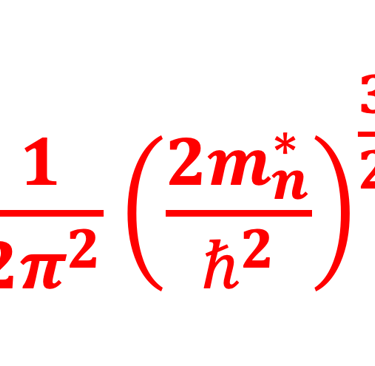
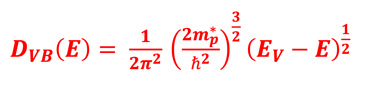
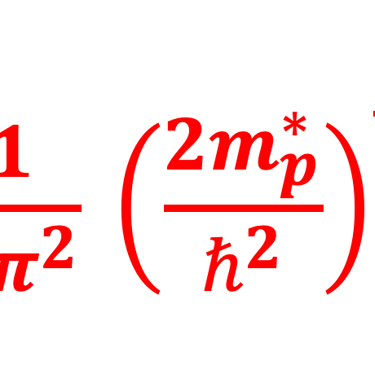
Le nombre d'électrons dans la BC et de trous dans la BV s'en déduit par une intégration sur BC et BV respectivement
Il faut bien entendu tenir compte de la probabilité d'occupation des électrons fFD(E) et des trous [1 - fFD(E)]
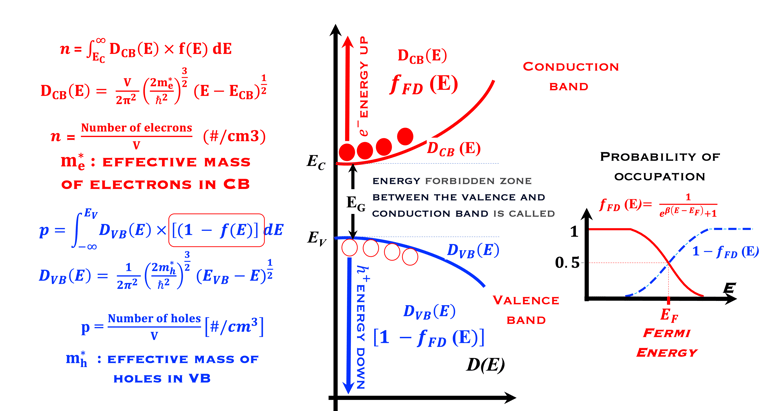
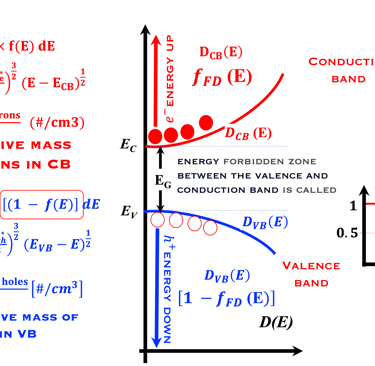
Quizzes
(1) Déterminer le nombre d'états quantiques [en centimètre cube] dans le silicium entre EC et EC + kT à T = 300 K. (2) Déterminer le nombre d'états quantiques dans le silicium entre ( EV +kT ) et EV
Calculer la probabilité qu'un état d'énergie supérieur à EF soit occupé par un électron. En supposant que T = 300 K, déterminez la probabilité qu'un niveau d'énergie 3kT au-dessus de l'énergie de Fermi soit occupé par un électron
Déterminer la température à laquelle il y a 1 % de probabilité qu'un état d'énergie soit vide. Supposons que le niveau d'énergie de Fermi d'un matériau donné soit de 6,25 eV et que les électrons (fermions) de ce matériau suivent la fonction de distribution de Fermi-Dirac. Calculer la température à laquelle il y a 1 % de probabilité qu'un état situé à 0,30 eV en dessous du niveau d'énergie de Fermi ne contienne pas d'électron
The distribution de Fermi-Dirac fFD(E, µ, T) ), appelée aussi nombre d'occupation donne la distribution des électrons dans les niveaux d'énergie E en fonction de la température, dans cette relation le potentiel chimique est le niveau de Fermi (EF = µ )
Tracer fFD(E, µ, T)
Quelle est la valeur de 𝒇(𝛍) ?
Trouvez la différence 𝜟E en énergie entre l'occupation électronique de 𝟏/𝟒 et l'occupation électronique de 𝟑/𝟒 en termes de 𝐤𝐁 𝐓.
Décrivez le comportement de la distribution de Fermi-Dirac à haute température
Qu'est-ce qui est correct ? T1 > T2 > T3 ou T1 < T2 < T3
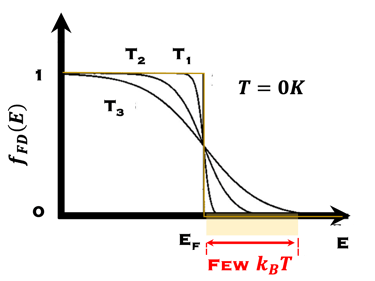
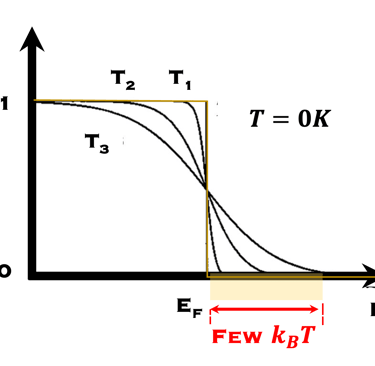
Transport sous l’effet d’un champ électrique
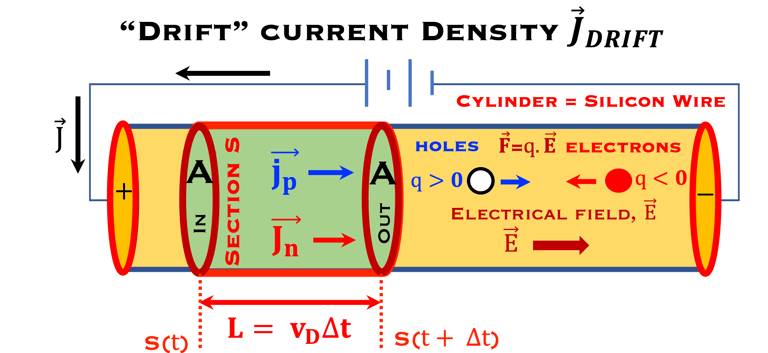
Nous considérons le flux de porteurs de charge traversant un cylindre de section A et de longueur L
Nous considérons le nombre d'électrons 𝒏) et (nombre de trous 𝒑) qui traversent la section Ain à t = 0 et qui arrivent à la section Aout pendant le temps ∆𝐭
∆𝐭 =𝐋/𝐯𝐃 avec ∆𝐭 temps [en s] nécessaire pour traverser l'élément de distance L, et VD étant la vitesse de dérive ou "drift velocity"
Le courant qui traverse ce cylindre est I = Q/∆𝐭 et la densité de courant est J = Q/(A . ∆𝐭)
Considérons le flux d'électrons (n): J peut s´exprimer en fonction du nombre n d'électrons qui se trouvent dans le cylindre de volume V = A . L pendant ∆𝐭 avec L = vD ∆𝐭
Nous allons établir d'une manière simple la densité de courant (J), la mobilité μ le champ électrique E
La mobility μ porteurs de charge est liée à la vitesse de dérive et au champ électrique par une relation simple
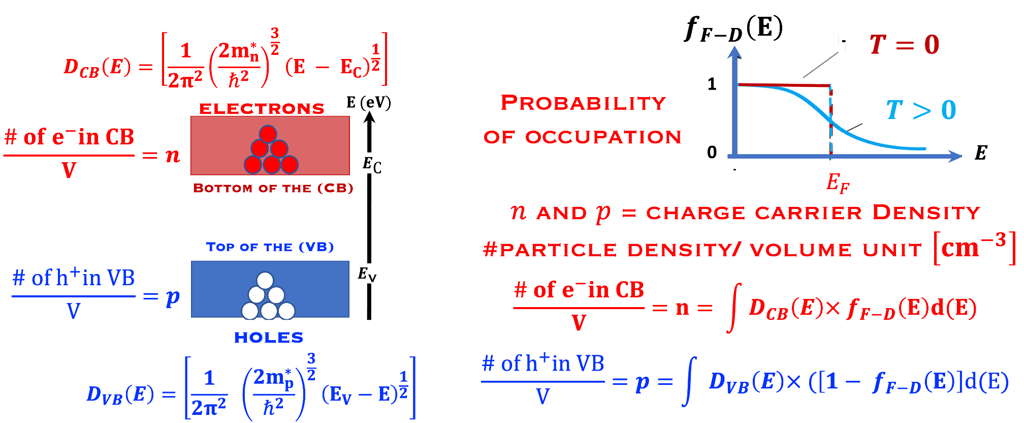
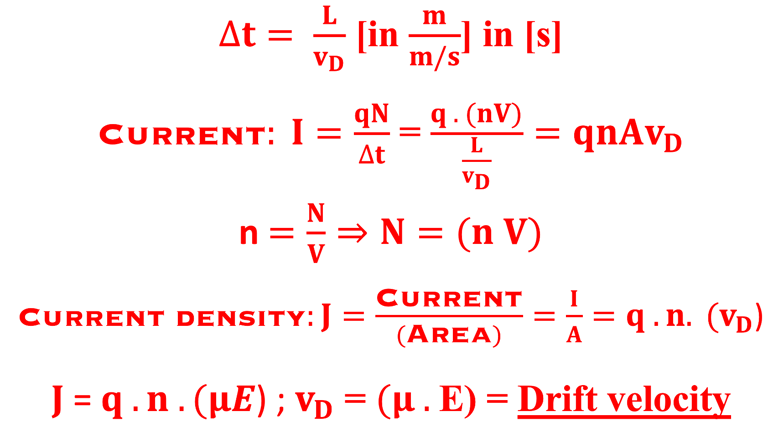
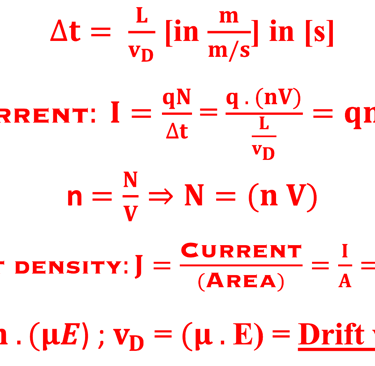
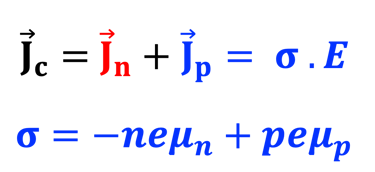
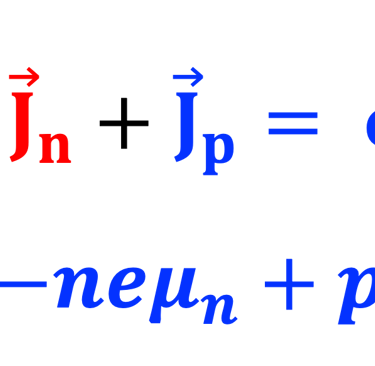
Retenez cette relation importante:
Jc est est le courant de conduction, σ est la conductivité du matériau, μn et μp sont respectivement les mobilities des électron det des trous
L'illustration ci-dessous montre la bande de conduction avec une densité d´électrons et la bande de valence avec une densité de trous
Jc est est le courant de conduction résultante de la conduction des électrons et des trous
σ est la conductivité du matériau, μn et μp sont respectivement les mobilities des électron det des trous
Transport sous l’effet d’un gradient de concentration
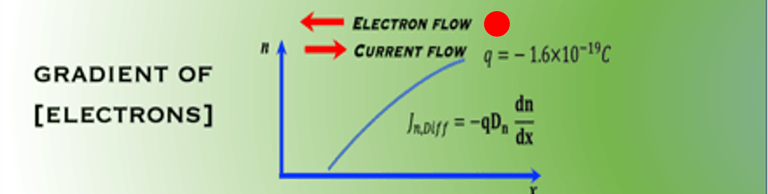
Le transport sous l’effet d’un gradient de concentration donne lieu à un courant appelé courant de diffusion
On peut additionner deux courant de diffusion: JD = JD,n + JD,p
Dp et Dn sont des coefficients de proportionnalité en [cm²/s]
Les électrons portent une charge négative, alors que les trous portent la même charge mais de signe opposé,
L'illustration montre le sens des courants induits par les électrons et les trous
𝑫𝒏 et 𝑫𝒑 sont liés à la mobilité par les relations d'Eistein: 𝑫𝒏 = kBT/q et 𝑫𝒑 = kBT/q

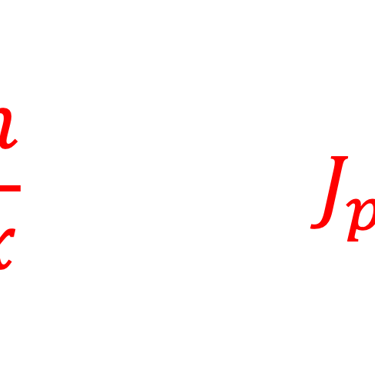
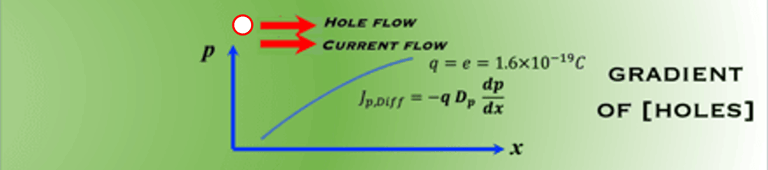
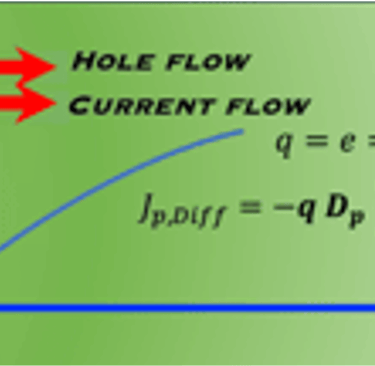
Densité de courant globale est la somme des courants de dérive et de diffusion
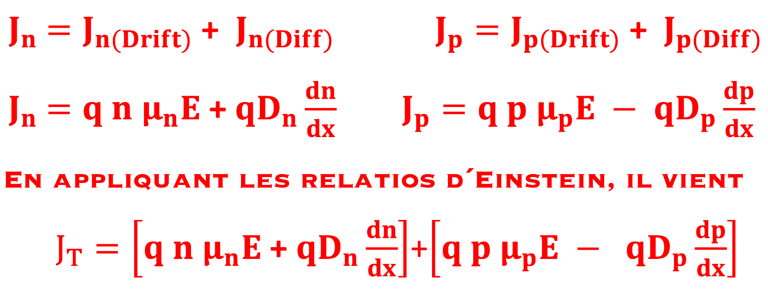
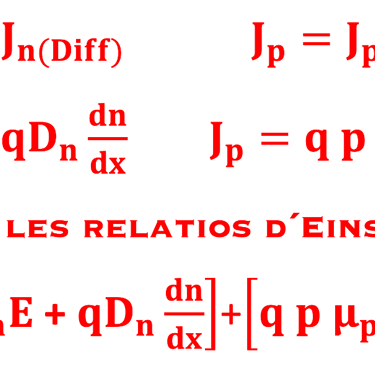
Dopage de type N (Exemple du Silicium)
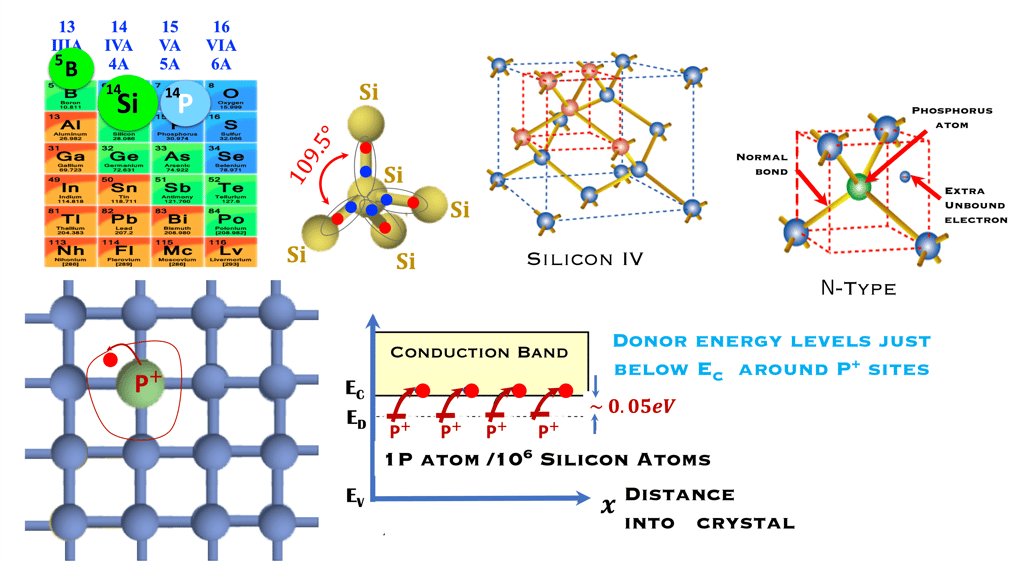
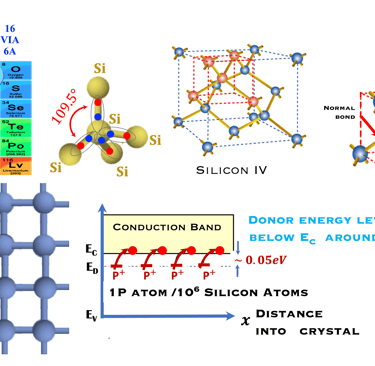
L'atome de phosphore introduit dans le réseau de Si apporte 5 électrons de valence permettant la formation de liaisons covalentes avec 4 atomes de silicium voisins
Le 5e électron est une charge électronique de conduction libre
Le silicium devient de type n et le phosphore est un dopage "DONOR"
Avant le dopage : 𝑛 = 𝑝 (un électron quitte derrière un trou)
Après le dopage:


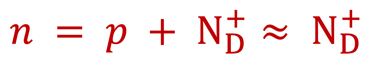
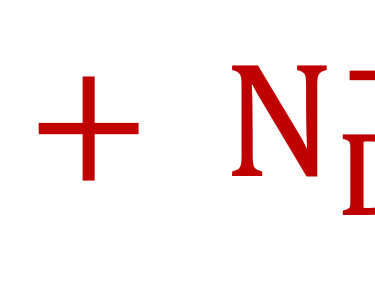

La conduction σn dans un semiconducteur de type n
La concentration de dopage pour le silicium est comprise entre:





Un semiconducteur dégénéré à température ambiante lorsque la concentration est :
Alors la concentration d'électrons (𝑛) dans le CB est presque égale à 𝑁𝐷, (𝑛 = 𝑁𝐷)
Lorsque 𝑁𝐷 >> 𝑛𝑖 à température ambiante:
La conductivité d'un semiconducteur de type n est résumée comme suit:
Dopage de type P (Exemple du Silicium)
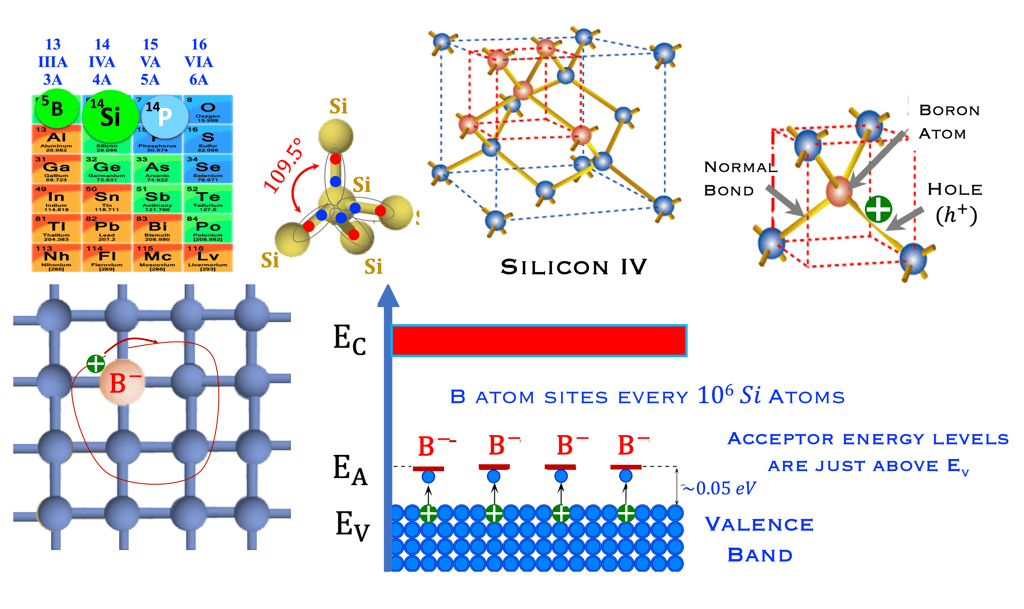
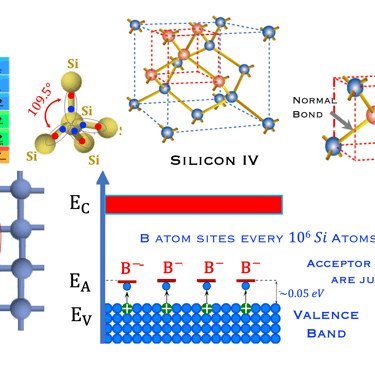
Introduire des atomes ayant un électron de moins que le silicium, tels que l'atome de bore (B, groupe III) qui a trois électrons externes seulement ne permet pas une substitution de huit électrons nécessaires pour que la couche soit complète, et conduit à un "TROU"
Le silicium devient de type P et le Bore est un dopage "Accepteur" dans le silicium qui devient de type P
Avant le dopage : 𝑛 = 𝑝 (un électron quitte derrière un trou)
Après le dopage:

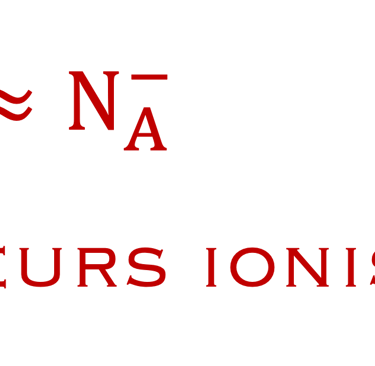


La conduction σp dans un semi-conducteur de type p
Nous supposons que NA ≫ ni (ni est la concentration intrinsèque)
Alors à température ambiante, la concentration de trous dans la bande de valence (VB) sera presque égale à NA, (c'est-à-dire p = NA)
Les trous de la VB se recombinent avec les électrons de la CB, afin de maintenir l'équilibre du système
Le tableau suivant résume la conductivité de type P dans le Silicium


Approximation de Maxell-Bolzmann
Probabilité d'occupation pour les électrons Quel que soit T
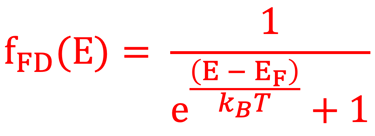
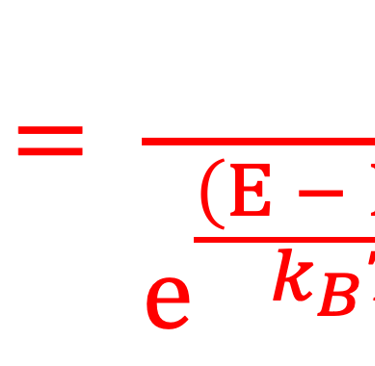
Probabilité d'occupation pour les trous est: [1-fFD(E)]
fFD(E) et [1 - fFD(E) ] sont symétriques par rapport à l'énergie de Fermi EF
T est la température du milieu ambiant en Kelvin et kB est la constante de Boltzmann
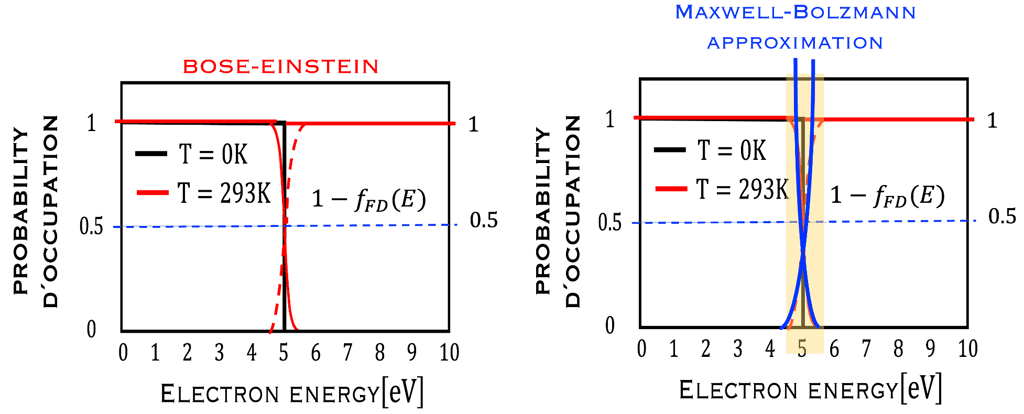
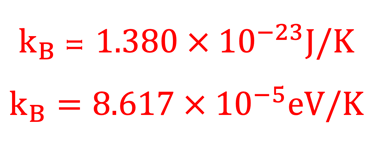
L´approximation de Bolzman comparée à celle de Bose-Eisteine est résumée comme suit:
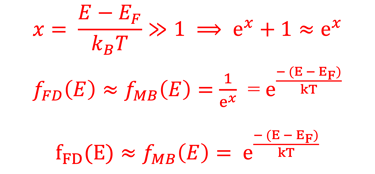
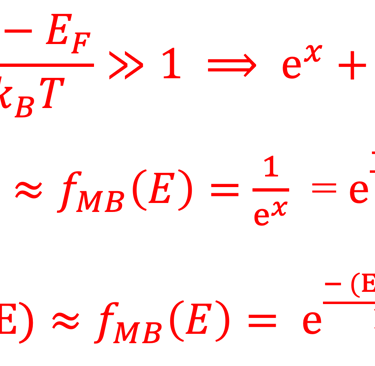
QUIZ: On considère une plaquette de silicium intrinsèque avec les caractéristiques suivantes:
On notera n, la densité d’électron dans la bande de conduction et p la densité de trous dans la bande de valence et on admettra que tous les atomes de dopants sont ionisés.
1) La plaquette dopée est-elle de type n ou de type p ? Justifier votre réponse
2) Écrire les expressions de la densité d’état dans la bande de valence DCB (E) et dans la bande de conduction DVB (E)
3) Que signifie un semi-conducteur intrinsèque.
4) donner les concentrations intrinsèques de quelques semiconducteurs étudiés?
5) Donner l’allure des courbes DCB (E), et DVB (E) au voisinage du minimum de la bande de conduction (CBM) et et du maximum de la bande de valence (VBM) respectivement
6) Expliquer, pourquoi le nombre total d’électrons dans la bande de conduction et celui des trous dans la bande de valence se mettront sous les formes intégrales


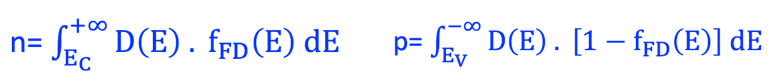
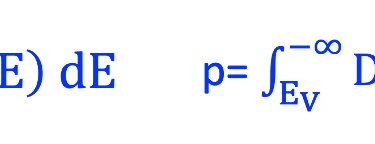
7) Nous supposons que le niveau de Fermi est situé à plusieurs kB . T en dessous de EC pour un semiconducteur de type n de sorte que la condition de maxwell Bolzman peut s´appliquer. Montrer que la concentrations n peut se mettre sous la forme:

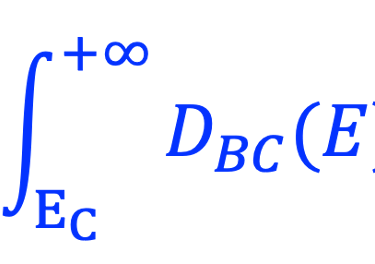
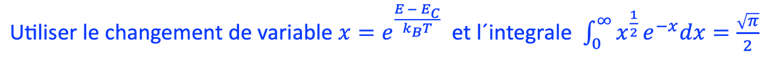
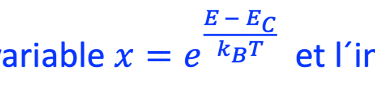
8) Montrer l'expression du nombre total de porteurs de charge dans la bande de conduction sous la forme

9) Procèder par une demarche similaire pour établir lesexpressions du nombre p, de trous dans la bande de valence et de la densité d’état effective Nv , des trous.

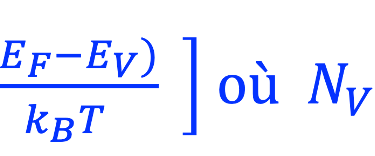
QUIZ: Dans un semiconducteur intrinsic le nombre n d´électrons par unite de volume dans la BC est égale au nombre de trous p par unite de volume dans la bande de valence. Écrire n = p =ni, pour intrinsic semiconducteur, et discuter la position du niveau de Fermi Ei d´un semiconducteur intrinsèque par rapport au milieu du gap
1) Montrer les expressions suivantes


2) On considère les deux types de dopage sont présents, Dans ce cas, l'impureté présente à une concentration plus élevée est déterminante du type de conductivité du matériau. On part du pricipe de la neutralité de charge: Charge totale négative + Donneurs ionisés = Charge totale positive + Accepteurs Ionisés, c'est à dire:
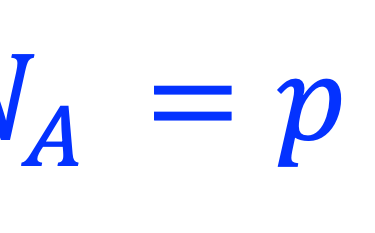
3) Montrer que la condition d´équilibre conduit pour un semiconduteur de type n, aux expressions suivantes:
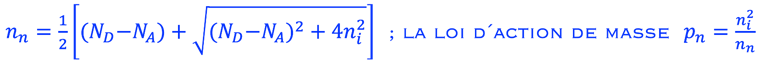
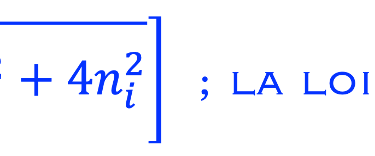
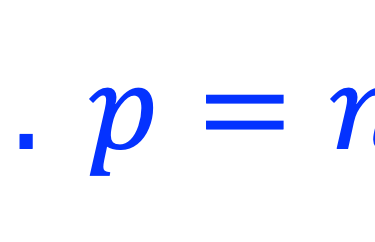
On utilisera la condition d´équilibre suivante:
4) Procéder par un raisonnement similaire pour obtenir la concentration des trous lorsqu’ils sont majoritaires (les électrons sont carrières minoritaires), etétablirles relation suivante
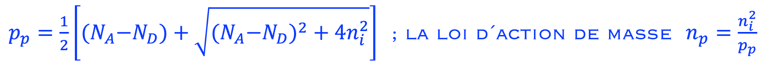
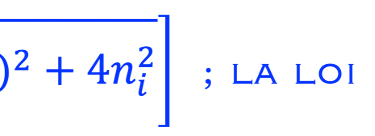
Attention, Nous utiliserons ici et dans tout ce qui suit les indice nn qui signifie les porteurs de charge (electrons) dans un semiconducteur de type n, alors que ici pn: signifie la concentration des trous qui sont minoritaires
Attention, Ici a concentration np est celle des electrons dans un semiconduteur de type p (les électrons sont les porteurs minoritaires)
Vérifier le calcul la position du niveau de Fermi


Ce calcul utilise l'équation du second degré pour obtenir la concentration des trous connaissant celle des électrons (dopage)


QUIZ: On considére un morceau de silicium est dopé avec du bore (B) et du phosphore (P) et tous les dopants sont ionisés et que la température T = 300 K
a) Ce matériau est-il de type n ou de type p ou n?
b) Calculez les concentrations de trous dans la bande de valence
c) Calculer les concentrations d'électrons dans la bande de conduction
d) Trouvez le niveau de Fermi (par rapport au bord de la bande de valence) de ce matériau. Exprimez votre réponse en termes de 𝑒𝑉 au-dessus de la bande de valence
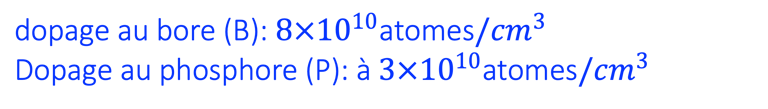


QUIZ: Trouvez la concentration de porteurs et le niveau de Fermi à la température ambiante (300K). Trouvez la concentration de porteurs et le niveau de Fermi à la température ambiante (300K) pour le silicium dopé au Phosphore avec:



Ce tableau compare trois semi-conducteurs Ge, Si et GaAs
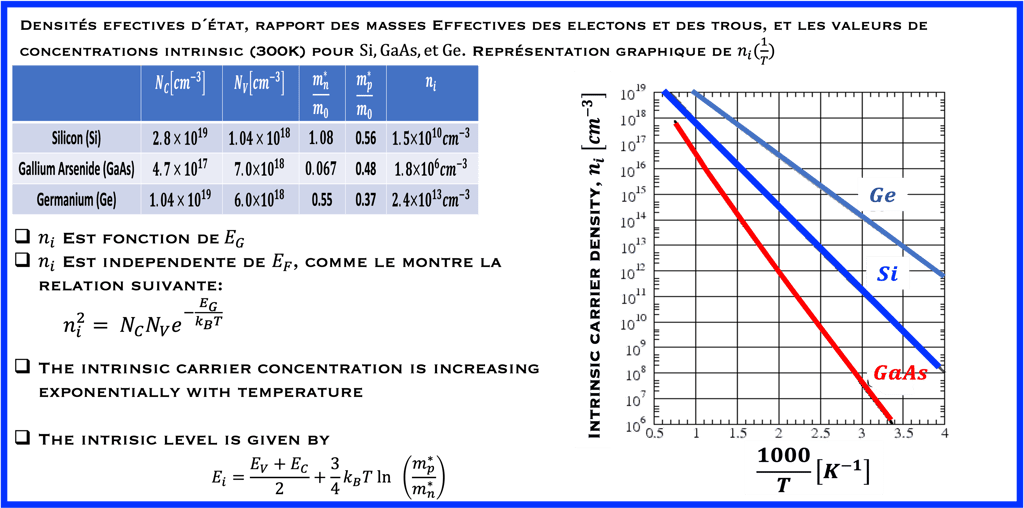
Se familiariser avec des calculs un peu compliqués
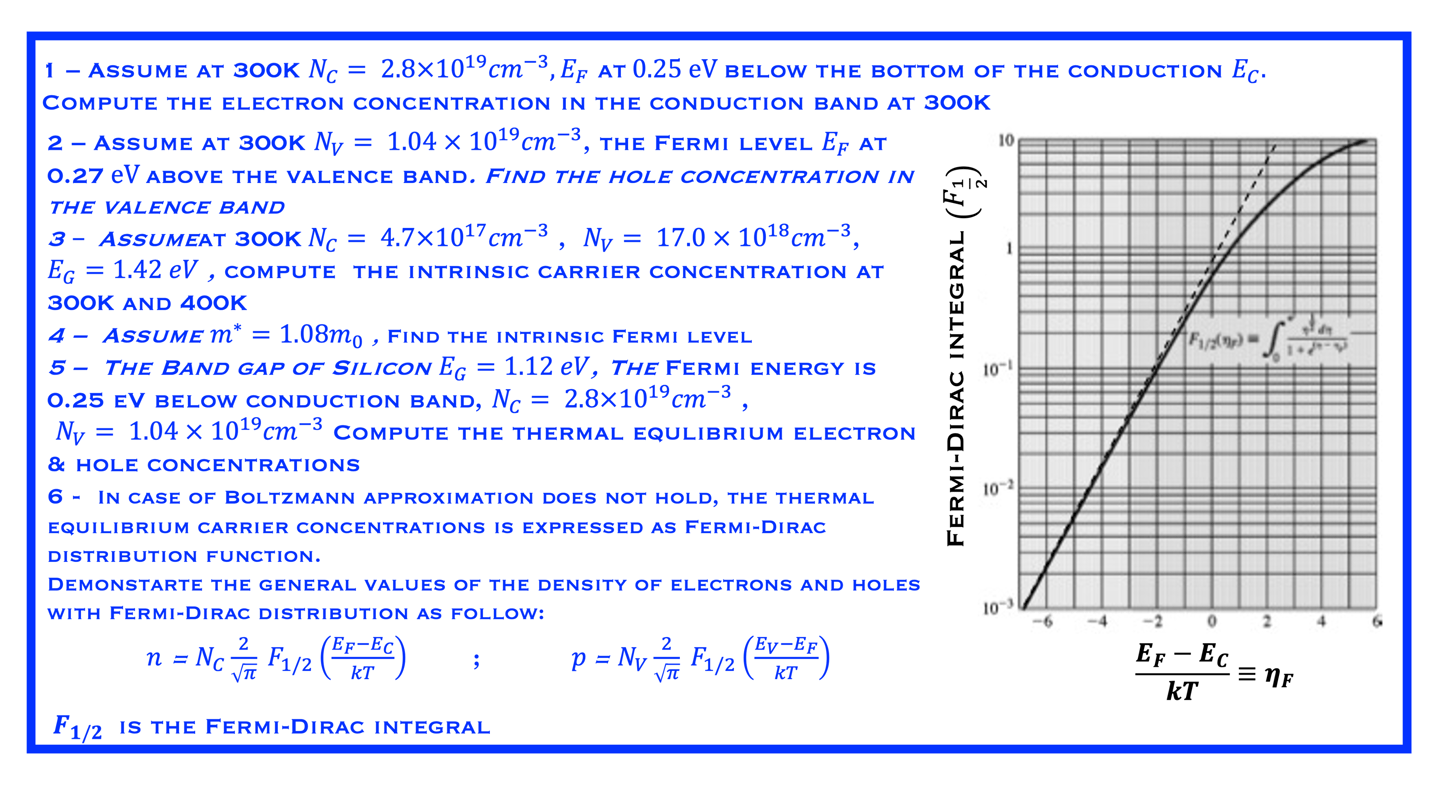
Regarder la video et ensuite interpréter chaque portion du graphe
Courtoisie de l'université de Perdue (Indiana) , cour du Prof.


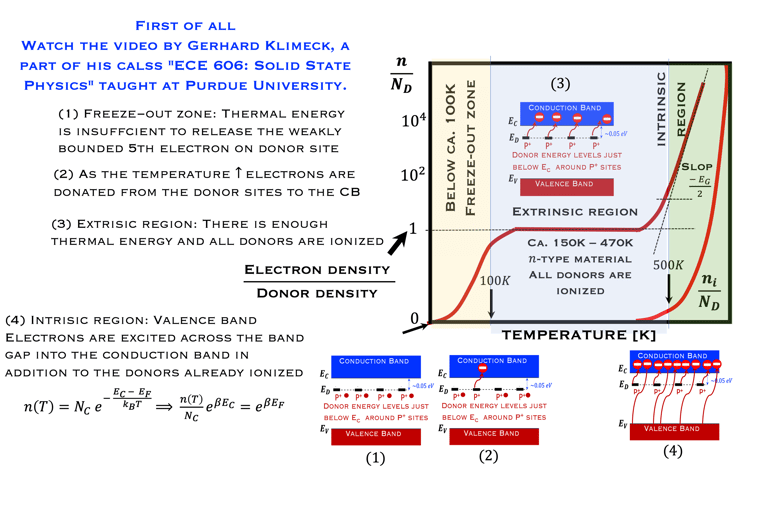
On distingue 3 régions :
(1) Très basses températures:
Peu de donneurs sont ionisés, et lorsque la température tend vers zéro, tous les donneurs deviennent neutres, c'est le régime de congélation des électrons.
(2) Températures basses (modérées):
La densité d'électrons à basse température est égale à la densité de donneurs
L'énergie thermique est suffisante pour ioniser tous les donneurs mais insuffisante pour créer un nombre conséquent de porteurs intrinsèques
Ce régime est appelé régime d'épuisement des donneurs
(3) Températures élevées:
Le régime est intrinsèque. Les donneurs ne jouent aucun rôle significatif. Le niveau de Fermi est exprimé par la relation
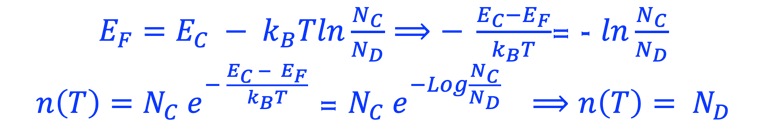
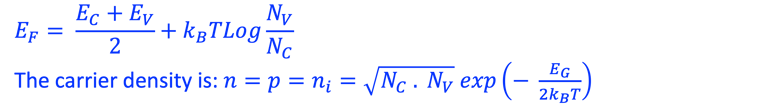
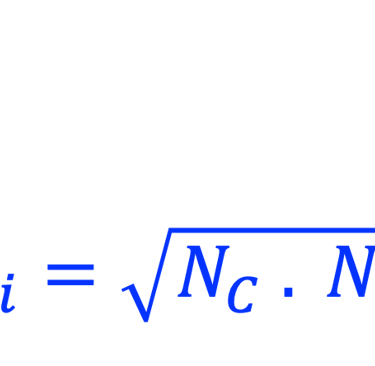
Source: S.M. Sze, Semiconductor Devices, Physics and Technology / Copyright ©️ 1985 Bell Telephone Lab. / John Wiley & Sons, Inc.
Comparison du Si et Ge
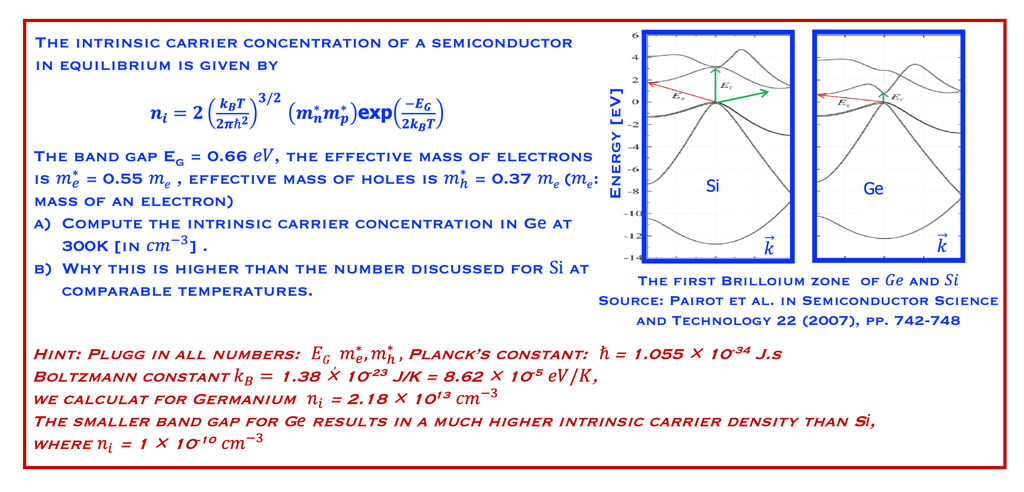
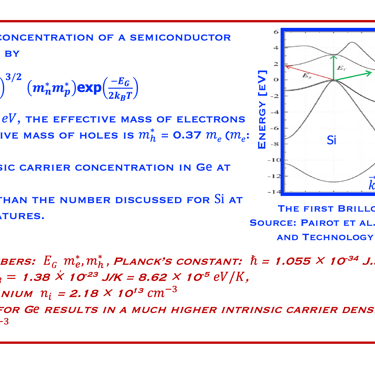
Technologies de dopage des cellules solaires
Industrie de la fabrication de plaquettes de silicium


Mettre en contact les deux types de silicium (type N et type P), pour obtenir une jonction P-N
En cours de construction

Nous recommandons de regarder la video par Dr. Jason Heikenfeld de "University of Cincinnati" avant de continuer de regarder les tableaux qui explique l'essentiel des jonctions P-N
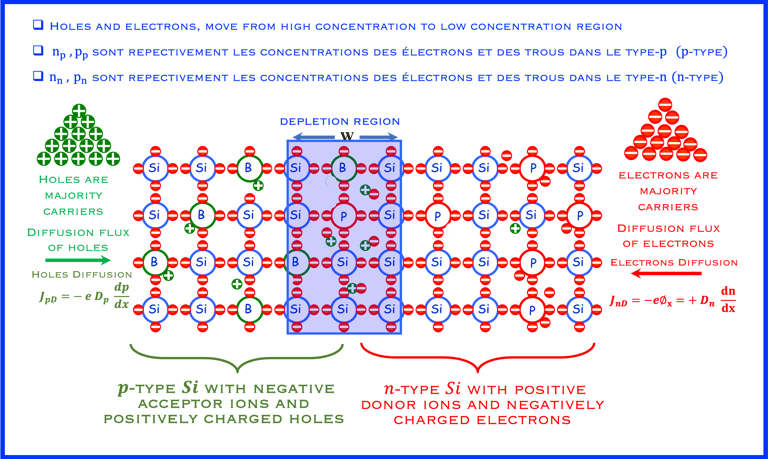
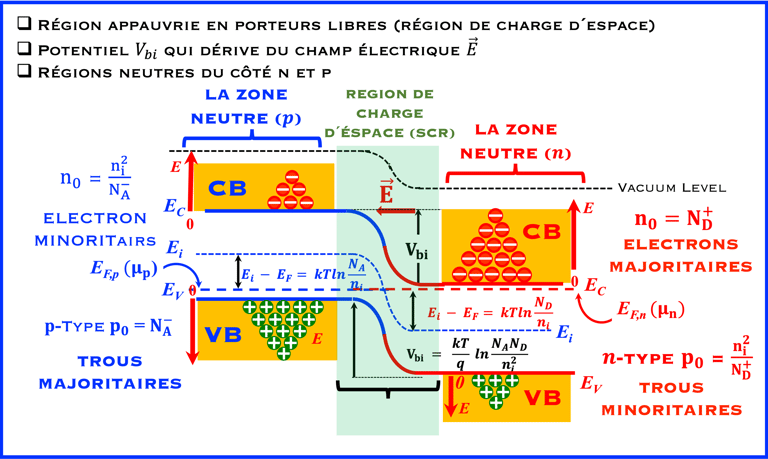
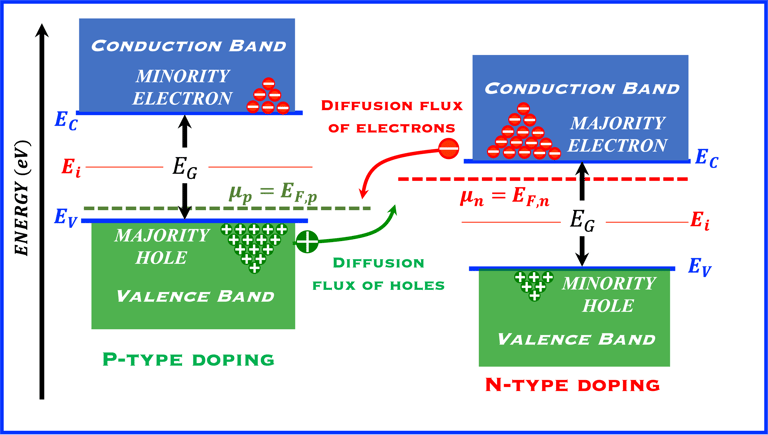
Une jonction PN peut être fabriquée en diffusant des donneurs (par exemple le phosphore), dans un semi-conducteur de type p
La conversion d'une couche d'un semi-conducteur de type N en type P avec des accepteurs (par exemple le Bore) créerait également une jonction PN
On suppose que les couches P et N sont uniformément dopées avec une densité d'accepteur NA et une densité de donneur ND, respectivement
Formation de la jonction en terme de diffusion des porteurs
Les électrons sont majoritaires dans le semi-conducteur de type N (dopage au phosphore, chaque P donne un électron)
Les trous sont majoritaires dans le semi-conducteur de type P (dopage au Bore, chaque B donne un trou ou manque d'un électron)
Les électrons vont migrer (diffuser) de la région N vers la région P
Les trous vont migrer (diffuser) de la région P vers la région N
Les électrons et les trous se combinent et il se forme une petite région proche de la jonction vidée en porteurs de charge mobiles
Formation d'une zone appauvri en porteur de charges entre deux régions neutres: N and P régions
L'illustration montre une étapes intermédiaires de la construction du diagramme de bande d'énergie
Le flux de porteurs de charge continue jusqu'à l'alignement des potentiels chimiques μp = μn et ce sont les niveaux de Fermi des l'électrons et des trous dans les régions N et P (EF,n = EF,p)
Nous avons illustrer avec des signes négatifs rouges les électrons majoritaires dans la BC du semi-conducteur de type N
Nous avons illustrer avec des signes positifs verts les trous majoritaires dans la BV du semi-conducteur de type P
Majoritaires et minoritaires se distingue par la quantité comme c'est indiqué dans l'illustration
L´équilibre se traduit par l'arrêt du flux d'électrons de N vers P et de trous de P vers N
Diagramme d'énergie de la jonction PN à l'équilibre
La jonction PN est caractérisée par trois couches :
La Zone N neutre (à droite)
La Zone P neutre (à gauche)
La région de déplétion (au milieu) entre les deux couches neutres N et P (appelée aussi région de charge d´espace RCE)
Dans RCE (en anglais Space Charge Region, SCR) règne un champ électrique et une barrière de potentiel est formée
Le champ électrique dérive (au sense mathématique du terme) du potentiel V
E = - (dV/dx)
Un potentiel intégré est développé à l'interface des deux matériaux différents matérialisé par Vbi qui dépend du dopage NA et ND
QUIZ: Exercice simple commenté
Dans chaque région (N et P), il existe un décalage de potentiel chimique qui correspond à la différence entre le niveau de Fermi intrinsèque avant le contact et après le contact
Nous appelons ce potentiel q∅n pour la région de type N et q∅p pour la région de type P (q étant la charge élementaire)
La densité électronique dans la région n et La densité de porteurs intrinsèques sont données par:
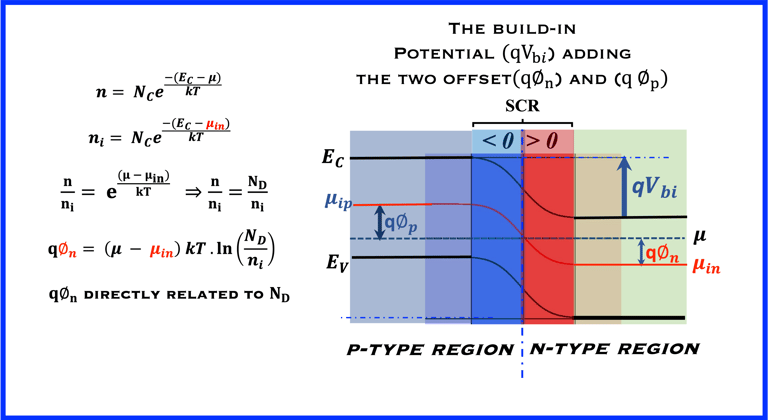
On peut faire le même raisonnement pour les trous dans la région P, calculez 𝑞∅𝒑 , et en déduire 𝑽𝒃𝒊 =∅𝒏 + ∅𝒑
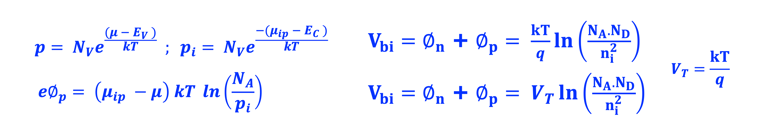
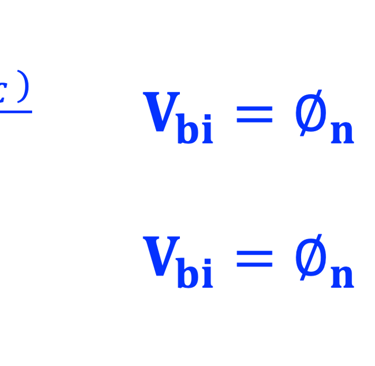
La tension d'intégration totale dépend à la fois du dopage du donneur ND et du dopage accepteur NA
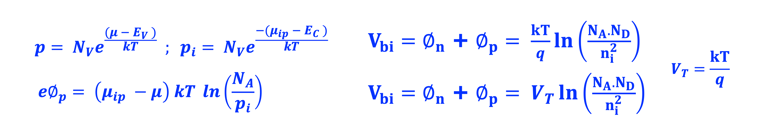
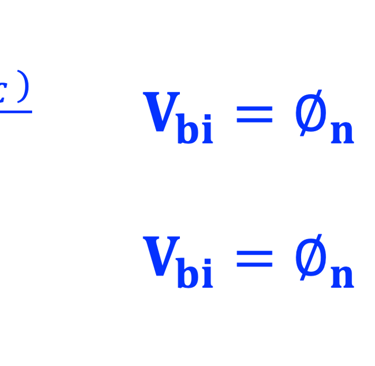
Nous allons résoudre sous forme d'exercice commenté, l'équation de Poisson pour une jonction P-N, pour aboutir au calcul de la largeur de la zone de charge d'espace, le champ électrique E(x), le potentiel V(x) et le potentiel intégré Vbi
QUIZ: (A) La concentration des électrons dans une plaquette de silicium intrinsèque de bande interdite EG = 1.1eV est:
On admettra que tous les atomes de dopants sont ionisés. La plaquette dopée est-elle de type n ou de type p ? Justifier votre réponse.
Utiliser la loi d’action de mass et l’expression de la neutralité électrique suivantes:
Pour établir l'équation de la forme:
On notera n, la densité d’électron dans la bande de conduction et p la densité de trous dans la bande de valence. On dope la plaquette avec
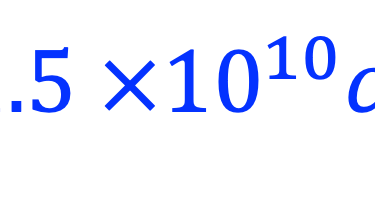

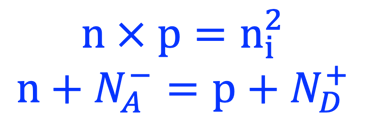
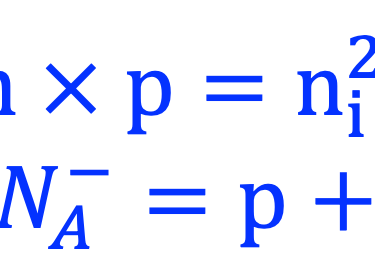
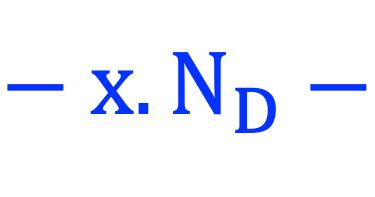
Ensuite, en déduire la concentration des électrons n et des trous p
N-B: On rappelle que l´on considère ici un semi-conducteur homogène où la somme de toutes les charges en tout point est nulle, la signification est simple: Le nombre de trous libres et de charges fixes positives balancé par le nombre d´électrons et de charge fixes négatives
QUIZ: (B) On introduit le bore (B) dans l’échantillon précèdent formant ainsi une jonction abrupte. Nous supposons que la concentration de B comme suit :

On admet que le champ électriqueE ⃗ dans la zone de charge d’espace (ZCE) est relié à la densité de charge 𝝆(𝒙) par l’équation de Poisson:
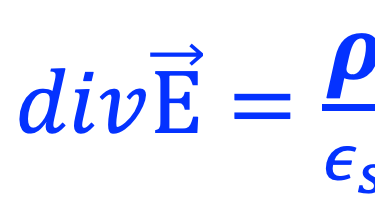
Cette relation s'écrit à une dimension sous la forme (comme illustré sur la figure ci-contre gauche)


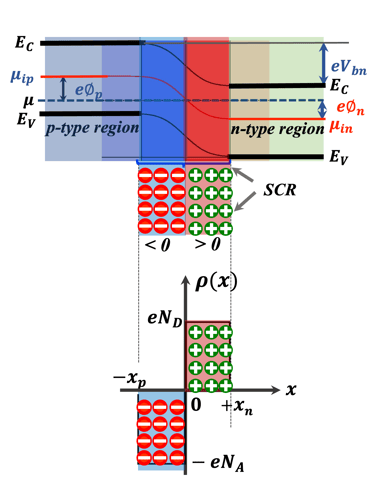
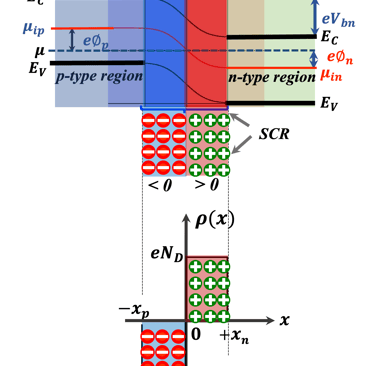
La figure ci-contre droite illustre les frontières de la zone de charge d’espace (ZCE) qui s’étend de -xp à 0 du côté P et de 0 à +xn du côté N
L’épaisseur W de la ZCE est W = (xp + xn )
La densité de charge ρ(x)
Le champ électrique E(x)
Le potentiel V(x) qui dérive de ce champs électrique: E(x) = - grad V(x)
Le potentiel intégré Vbi, est le maximum que Lyon peut atteindre
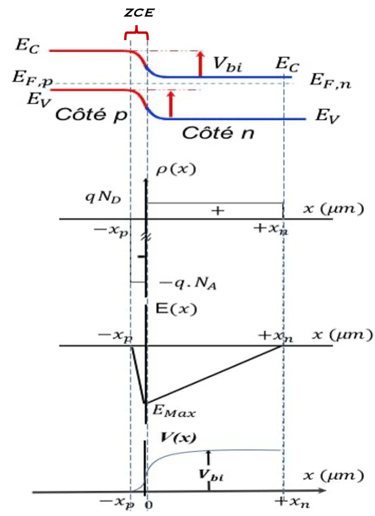
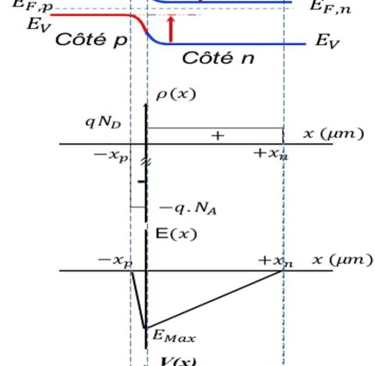
montrer que la distribution du champ électrique E(x) à l’intérieur de la zone de charge d´espace (ZCE) peut se mettre sous la forme :
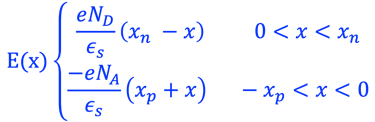
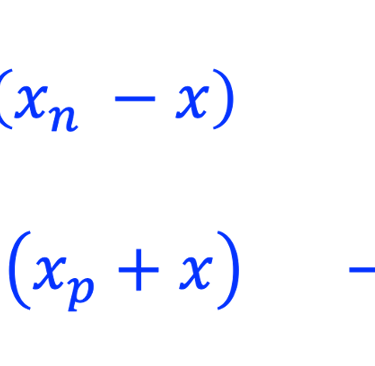
Quelle est la valeur du champ électrique maximum Emax = E(x = 0)?
Indication
La plaquette dopée au P est de type N en effet:
L´atome de phosphore (P) ayant 5 électrons dans sa couche de valence est introduit dans le réseau du silicium (Si), quatre atomes de Si formeront des liaisons covalentes avec avec quatre des 5 électrons de valence que possède l’atome de P ..
Comme il y a quatre liaisons covalentes (et donc huit électrons) entourant immédiatement l’atome, la couche de valence est pleine et ne peut plus contenir le dernier électron de l’atome de phosphore
L´électron supplémentaire de P est à l’état libre, alors chaque atome de phosphore incorporé ajoute 1 électron libre au réseau du silicium.
Le silicium (Si) est donc dopé N et le dopage est de

La loi d'action de masse et la condition de neutralité sont applicables
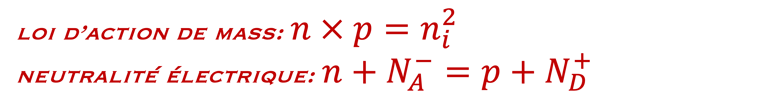
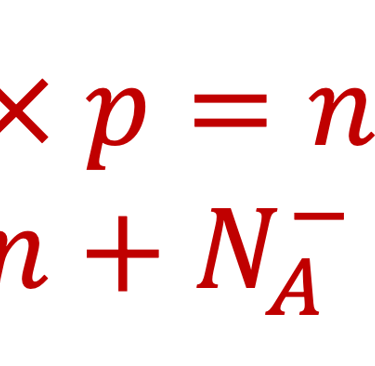
Comme on a pas de dopage accepteur jusqu'à`ce point (NA = 0)
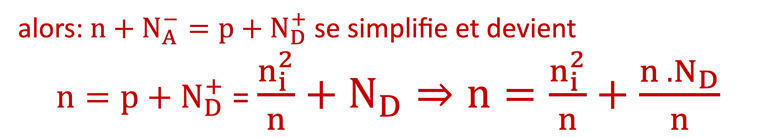
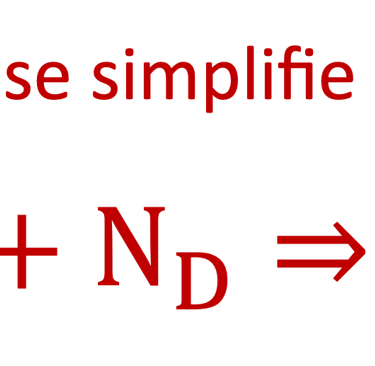
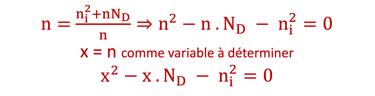
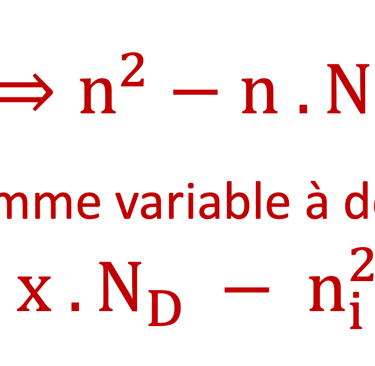
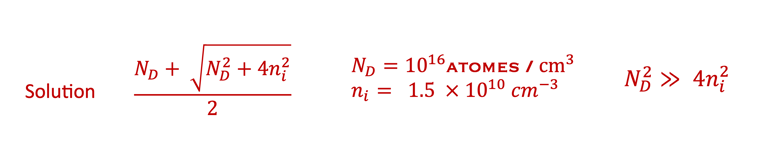
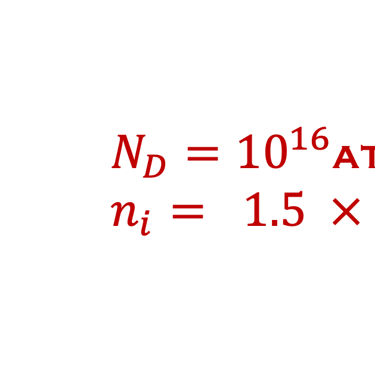
𝑛 = ND la densité d’électrons (Donneur) On applique la loi d’action de mass:
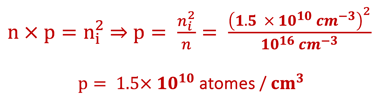
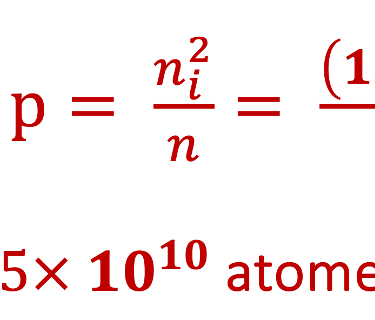
On introduit le bore (B) dans l’échantillon précèdent de type N déjà dopé au (P) formant ainsi une jonction abrupte
La concentration de bore est de :
Le champ électrique dans la zone de charge d’espace (ZCE) est relié à la densité de charge 𝝆(𝒙) par l’équation de Poisson:


Lorsqu'on met en contact un semi-conducteur type N et un semi-conducteur type P du même matériau (le silicium par exemple), la différence des densités de donneurs et d'accepteurs ‖ND-NA ‖ passe "brusquement" d'une valeur négative pour la zone P, à une valeur positive pour la zone N
Une barrière de potentiel est formée pour les trous et les électrons
Il se forme aussi une zone de charge d´éspace (double couche de charges négatives P coté et positives coté N), dans laquelle règne un un champ électrique qui dérive d´un potentiel E = - dV/dx
E(x) s'obtient en intégrant dans les deux intervalles 0< x <xn et -xp<x<0
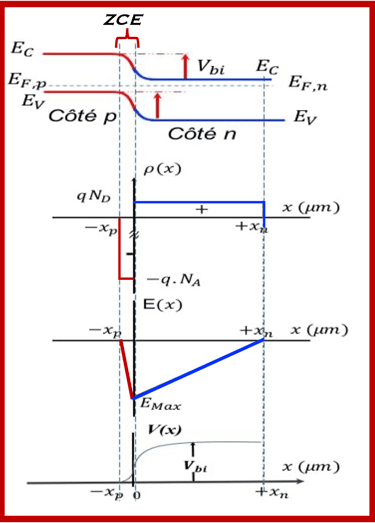
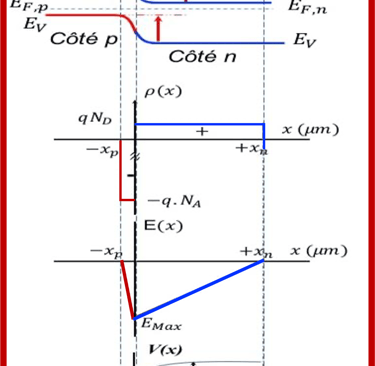
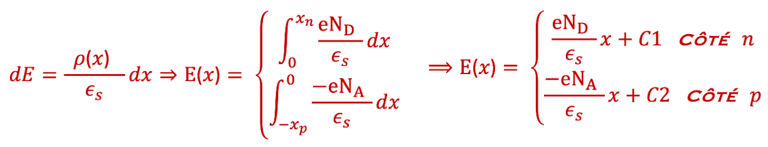
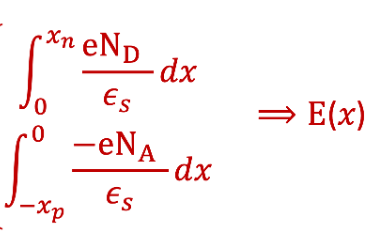
Pour calculer les constantes d´intégration C1 on écrit E(xn ) = 0
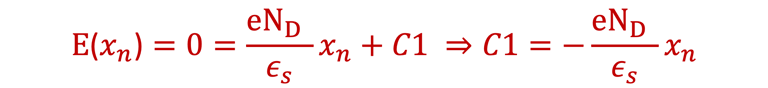
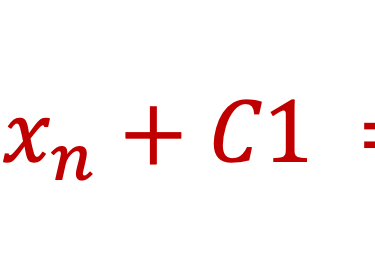
L´expression du champs electrique dans la zone N est
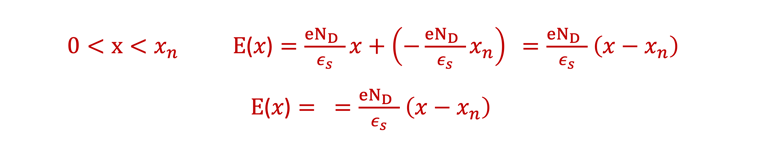
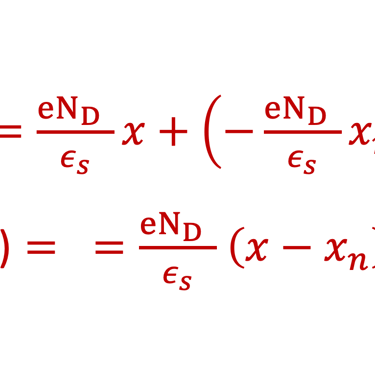
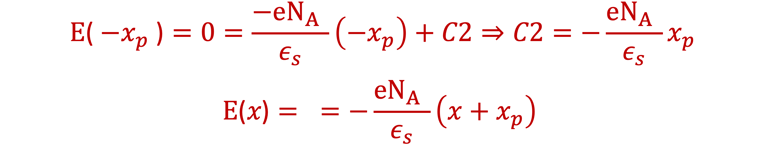
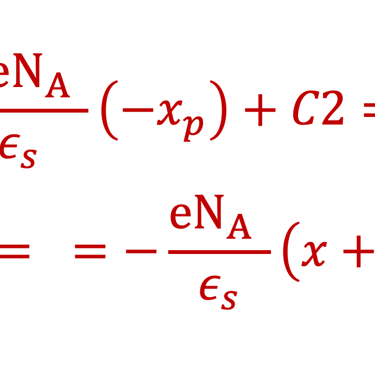
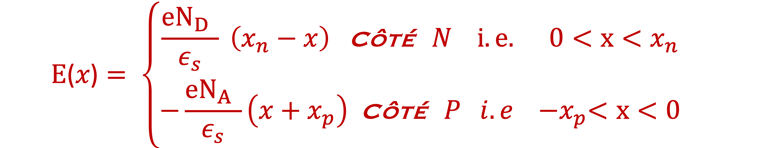
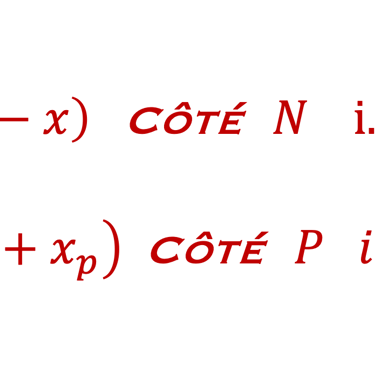
Le même calcul de C2 d´effectue du côté P en calculant E(x = -xp)
Champ électrique dans ZCE
En tenant compte de la condition de neutralité on peut calculer xp et en déduire W = xn + xp (voir illustration)
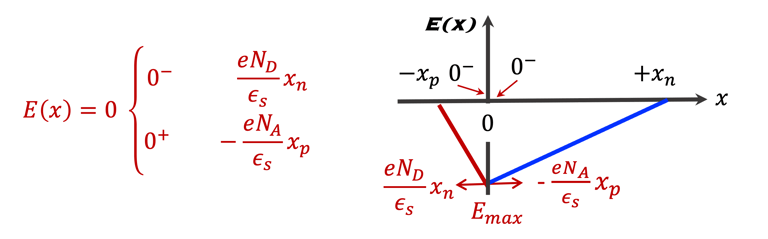
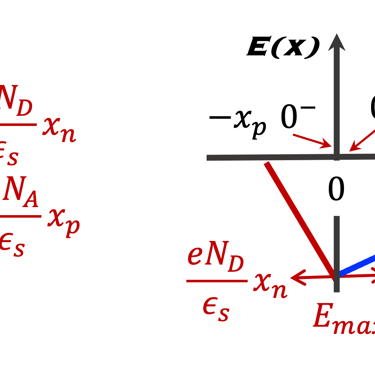
L'illustration ci-dessous montre comment calculer Emax = E(x=0)
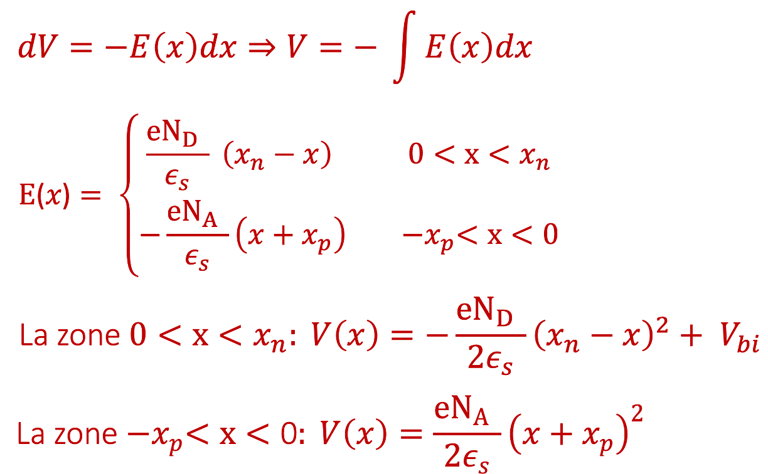
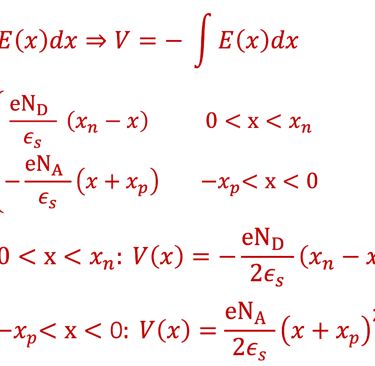
Le potentiel V(x) et le champs électrique sont reliés par la relation: E(x)=-dV/dx (le champs électrique dérive du potentiel V(x))
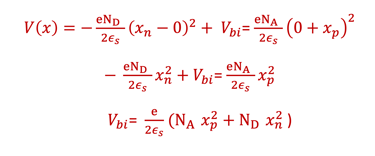
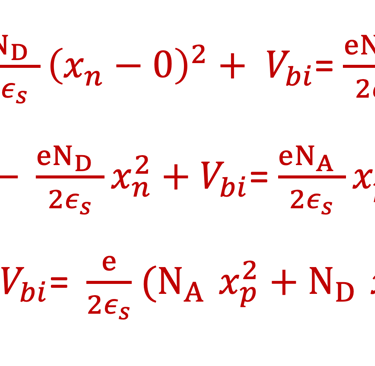
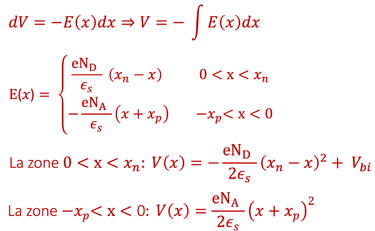
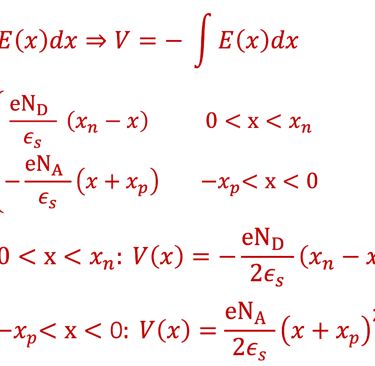
Détermination de Vbi et l’épaisseur de la zone de charge d´espace ZCE (W)
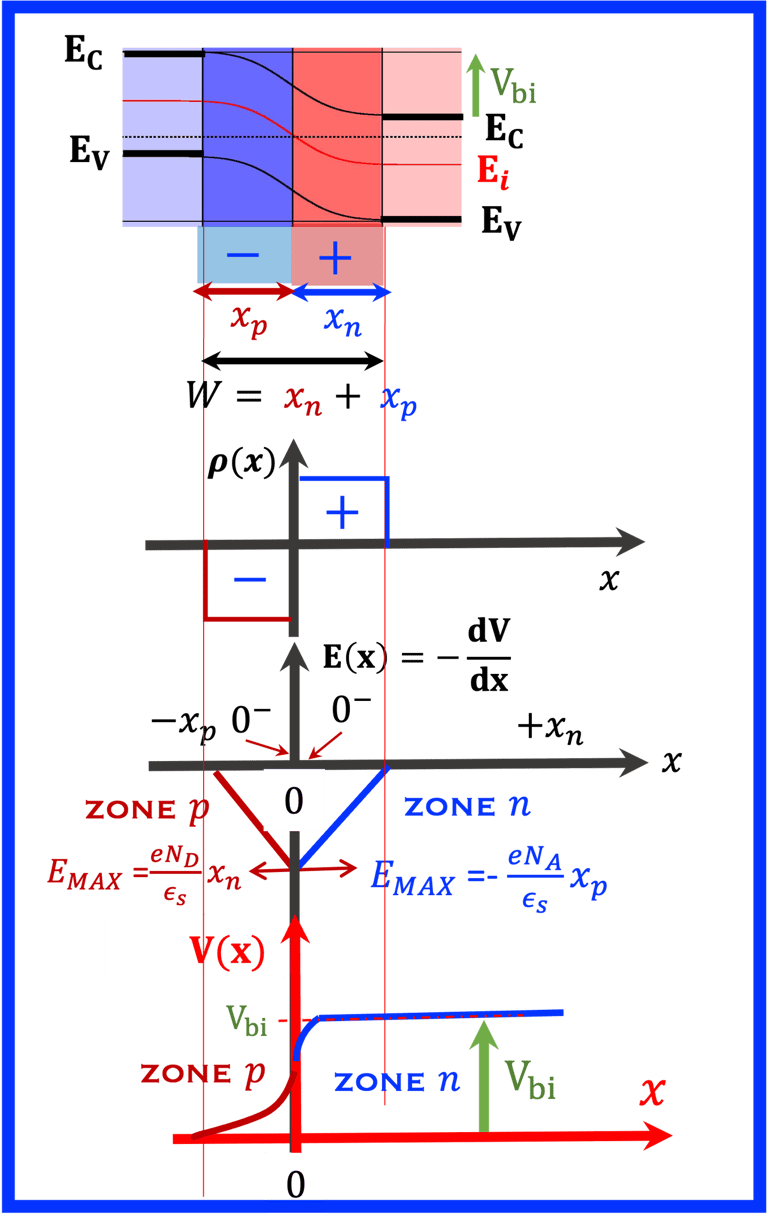
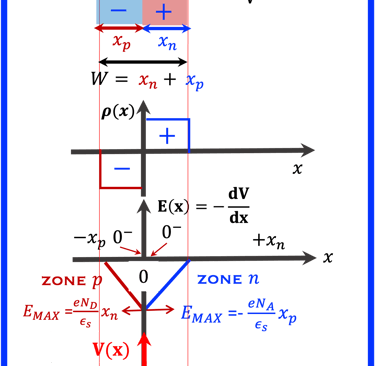
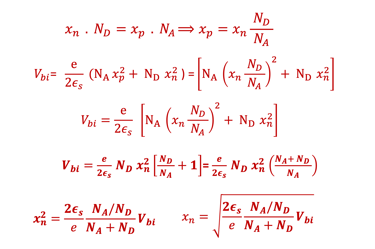
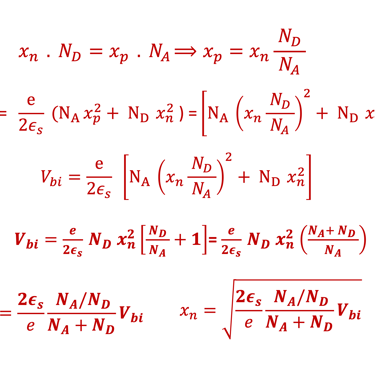
On doit ajouter la condition de neutralité dans ZCE: xn . ND = xp . NA
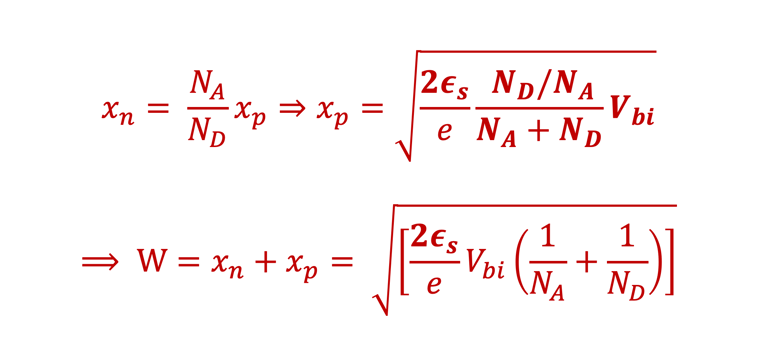
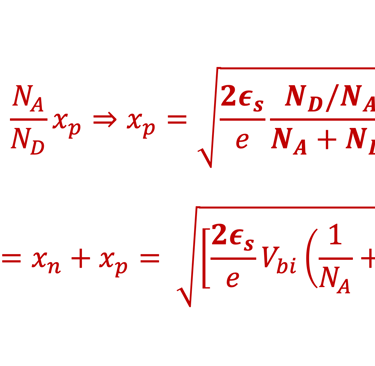
Application numérique

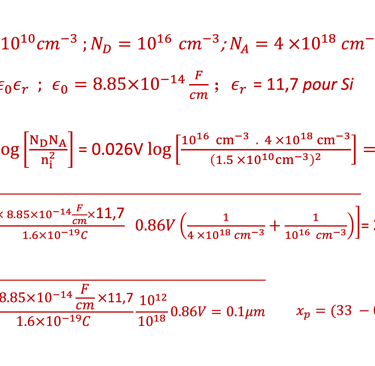
Regarder les vidéos de Mark Lundstrom at Purdue University avant de continuer


Relations et notations utilisées dans l'étude de la jonction en équilibre , hors d´équilibre et dans l'établissement et la résolution de l'équation de continuité
Nous rappelons ici que les densités d’électrons et de trous des deux côtés de la jonction sont reliées par le potentiel Vbi par les relations suivantes
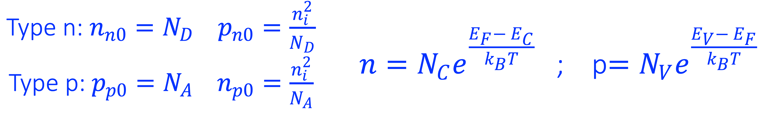
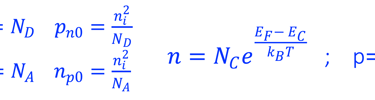
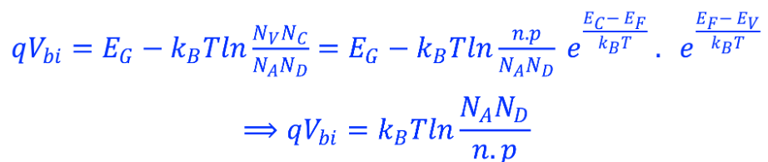
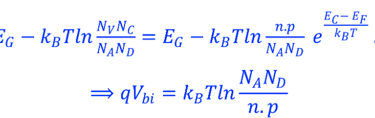
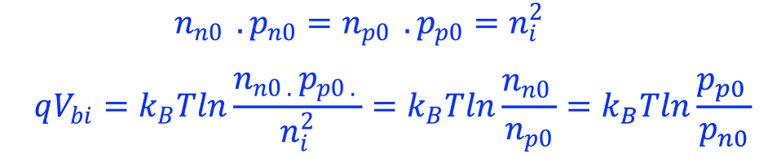
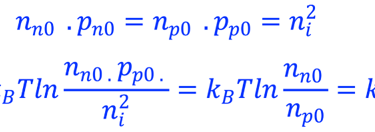
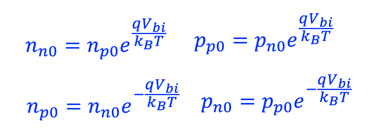
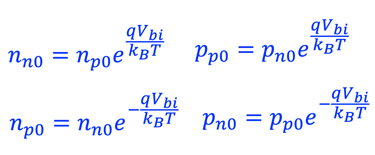
Dans une ne jonction à l'équilibre: le courant de dérive compense exactement le courant de diffusion
La hauteur de barrière de potentiel en unité d'énergie est qVbi ou eVbi)
On admet que toutes les impuretés (dopages) sont ionisées et on utilise par la suite les notations ND et NA
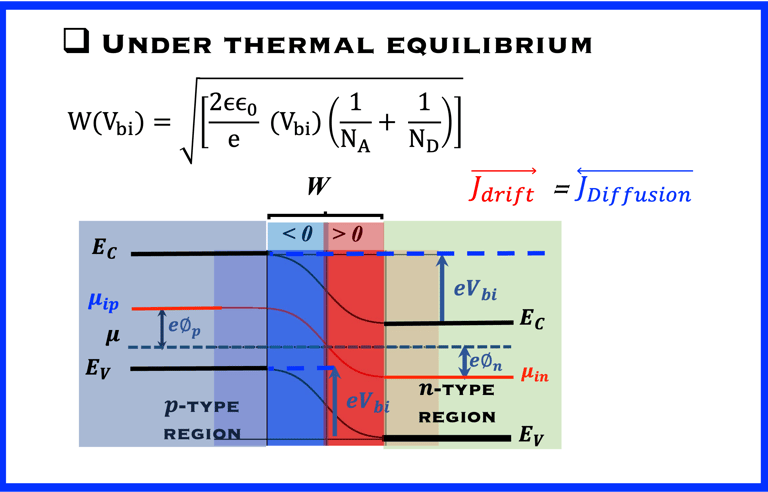
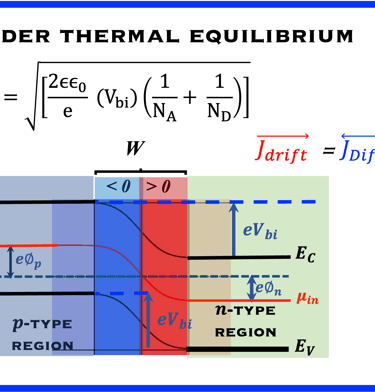
qVbi = EG -(Ec - EF)n - (EF - EV)p


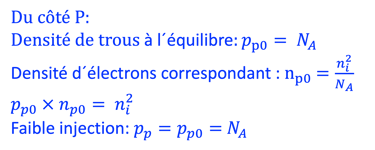
Ce qu'il faut savoir sur la jonction PN à l équilibre (résumé au tableau)
les trous de la zone P ayant diffuser vers la zone N, deviendront minoritaires dans cette zone
Les électrons de la zone N ayant diffuser vers la zone P deviendront minoritaires dans cette zone
Une barrière de potentiel qui en résulte, stope la diffusion des porteurs majoritaires, le champ électrique E (x) = − Grad V(x) qui s’oppose à la diffusion
Une région sans porteurs de charges appelée zone de charge d’espace noté ZCE est formée entre les deux régions neutres P et N
L´'hypothèse que tous les atomes dopants (NA et ND) sont ionisés
La concentration d'électrons et de trous n et p est définis par les dopages ND et NA respectivement
On établit écrit l’´equation de Maxwell-Gauss div E(x)= ρ(x) /ε ( donnée ici à une dimension par soucis de simplicité)
On tient compte de la relation E (x) = − Grad V(x)
Le modèle d'une jonction abrupte consists en une variation discontinue de la densité de donneurs et d’accepteurs de part et d’autre de la jonction
Les densités de porteurs aux extrémités de ZCE sont discontinues
L´intégration et en utilisant les conditions aux limite de la zone de charge d'espace on obtient E(x), V(x), et Vbi
L'épaisseur de la charge d'espace W est aussi calculable en fonction de Vbi, ND et NA
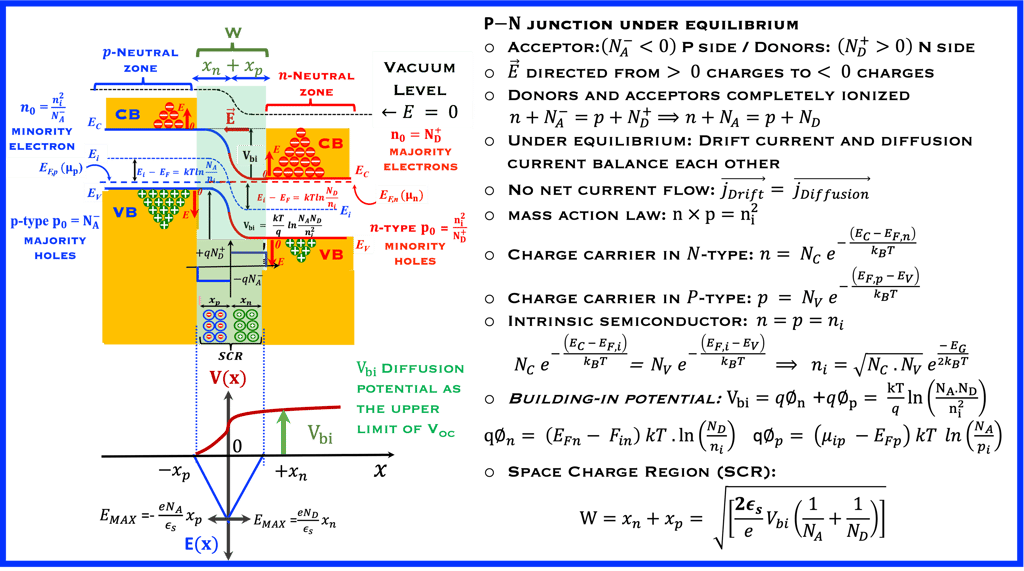
La jonction P-N hors d'équilibre
Les relations précédentes s´appliquent lorsqu'on applique un potentiel extérieur Va à la jonction
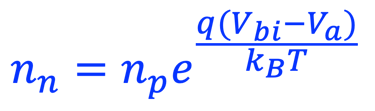
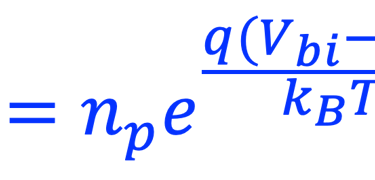
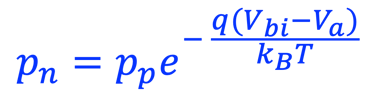
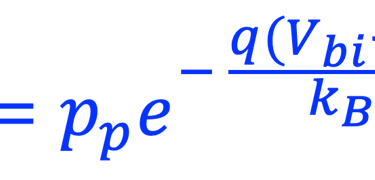






On applique une tension extérieure Va opposée au potentiel de barrière à l'équilibre ( ce qu'on appelle ici polarisation directe)
Il en résulte une diminution de la barrière de potentiel de la jonction qui devient (Vbi-Va) au lieu Vbi
La région de charge d'espace (Space charge region, SCR) se rétrécit et devient W(Vbi-Va)
Polarisation direct signifie:
La zone N est connecté à la borne négative
La zone P est connecté à la borne positive
Il en résulte une diffusion des porteurs majoritaires: les électrons de la zone N vont vers la zone P et les trous de la zone P vont vers la zone N
Les électrons provenant de la source (borne négative) s'ajoutent à ceux de la zone N
Certains vont se recombiner aux trous proches de la jonction,
Les autres se déplacent de trou en trou pour revenir vers la source (borne positive)
Les trous positifs issus de l´ionisation des accepteurs se déplacent de la zone P vers la zone N
Les trous se recombinent avec les électrons libres restés dans cette zone (n'ayant pas franchi la barrière de potentiel)
L'épaisseur de la ZCE est fonction de (Vbi - Va)
Deux types de courant:
- le courant de diffusion de minoritaires : IDiff = IDiff(électrons) + IDiff(trous)
- le courant de recombinaison IR
Deux quasi-niveaux de Fermi traduisent la répartition des porteurs dans la RCE
Quasi-niveau de Fermi des électrons: EFn
Quasi-niveau de Fermi des trous: EFp
La différence entre les niveau de Fermi des électrons et des trous est: qVa = EFn - EFp
La barrière de potentiel en volt est: (Vbi - Va )/q (q étant la charge de l'électron)
L'épaisseur de charge d'espace change W, devient:
Nous avons illustre la situation hors d'équilibre sur le schéma ci.dessous
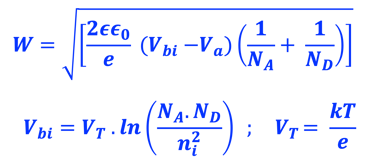
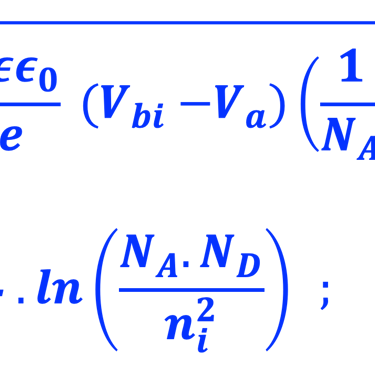
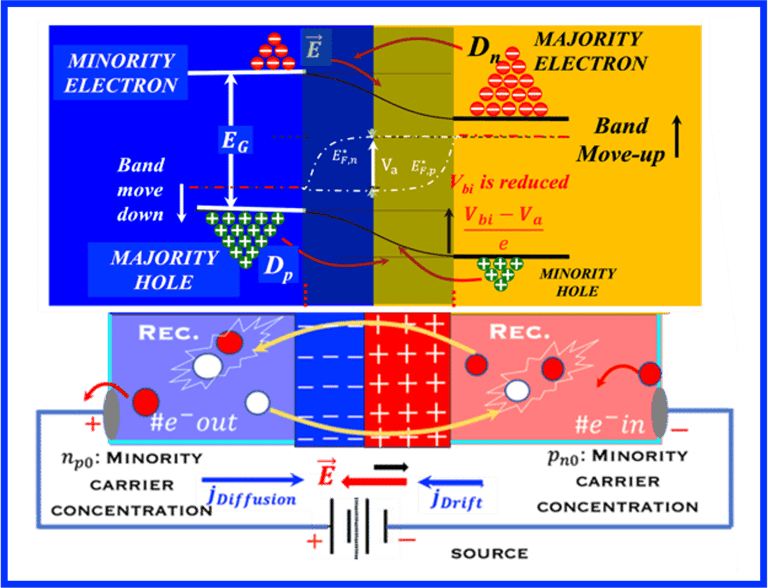
Les courants de diffusion des porteurs minoritaires seront formulés par les équations de continuité
Quelle est la variation du nombre de porteurs de charge dans un volume élémentaire ∆V = A . ∆x ?
Le volume élementaire A . ∆x peut correspondre à la zone P et N d'une jonction P-N
Admettons que le nombre électrons (n) dans ∆V = A . ∆x augmente par génération ou diminue par recombinaison
(∂n/∂t) . A . ∆x exprime la variation du nombre d'électron dans le temps dans l'élément de volume ∆V
(∂n/∂t) . A . ∆x = [(J(x)/q) A] - [(J(x+∆x)/q) A] + [Gn . A . ∆x] - [Rn . A . ∆x]
[(J(x)/q) A] est le Flux d'électron entrant (en x) par la section A
[(J(x+∆x)/q) A] est le Flux sortant (en x+dx) par la section A
[Gn . A . ∆x] est le nombre électrons généré dans le volume élémentaire ∆V
[Rn . A . ∆x] est le nombre électrons qui se recombine dans le volume élémentaire ∆V
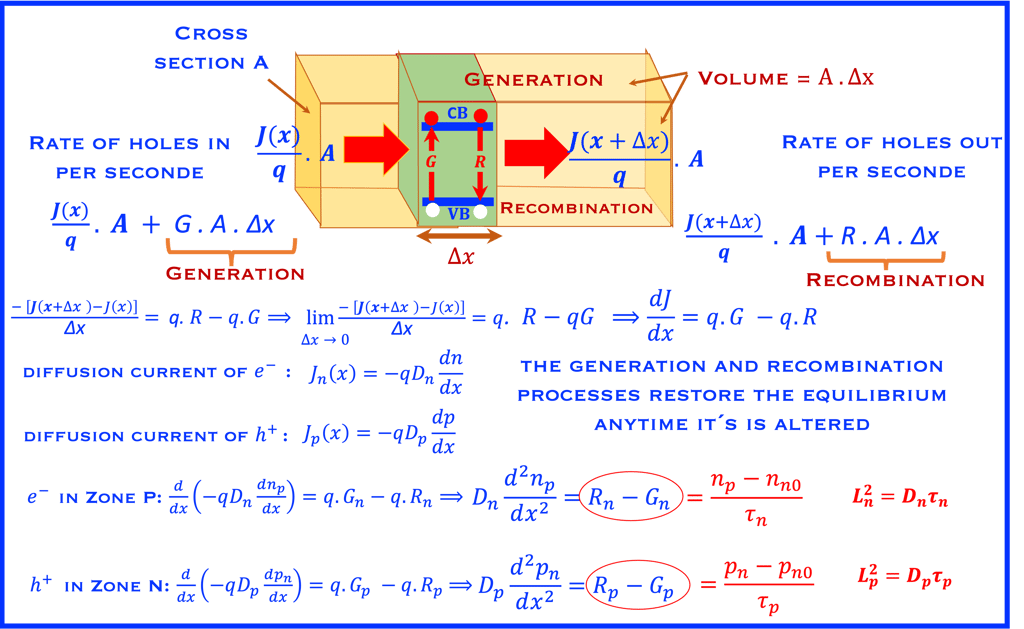
La résolution des équations de continuité
Il n'y a pas de champ électrique dans la région quasi-neutre:,
Les équations de densité de courant des porteurs se réduisent à des termes de diffusion:
pn pour les trous dans la zone N
np pour électrons dans la zone P
pn et np sont calculés séparément our les deux régions P et N respectivement
Jn(x) et Jp(x) sont données dans le tableau ci-dessus
La variation dans le temps du courant traversant l'élément de surface A est:
(∂n/∂t) . A . ∆x = [(J(x)/q) A] - [(J(x+∆x)/q) A] + [Gn . A . ∆x] - [Rn . A . ∆x]
⇒ (∂n/∂t) = ([(J(x)/|q|)] - [(J(x+∆x)/|q|)]/ ∆x + Gn - Rn
On prends ∆x→0 (infiniment petit), de sorte que:
(∂n/∂t) = (1/|q|) [dJn(x)/dx] + Gn - Rn ici q est la charge de l'électron (négative)
Une équation similaire peut être établie pour les trous:
(∂p/∂t) = (1/|q|) [dJp(x)/dx] + Gp - Rp. ici q est la charge du trou (positive)
Rappelons que:
les trous minoritaires à l'équilibre sont notés pn0
les électrons minoritaires à l'équilibre sont notés np0
Nous adoptons un modèle simple pour la génération-recombinaison
Un chapitre sera consacré pour les mécanismes de génération-recombinaison dans ce cours
Ce model stipule que (R-G) est proportionnel à l'excès de densité de porteurs
On peur envisager l´absence de génération (G = 0) ou l'absence de recombinaison (R = 0)
Le tableau ci-dessus résume les calcules pour aboutir à l'équation de continuité
Les indications essentiels nécessaire pour la résolution des équations de continuité sont données dans le tableau
Conditions de faible injection: Les densités de porteurs majoritaires ne sont pas affectées
Le taux de génération de recombinaison (R-G) des porteurs minoritaires dépend fortement de l'injection
Rn = Δn/τn
Rp = Δp/τp
n´= Δn = (np - nn0) est la concentration excédentaire d'électrons dans la zone P par rapport à l'équilibre np0
p´= Δp = (pn - pn0) est la concentration excédentaire des trous dans la zone N par rapport à l'équilibre pn0
( np , pn ) sont continuellement générés et recombinés
Le retour à l'équilibre se fait avec les temps caractéristique τn et τp
τn constante de temps pour les électrons
τp constante de temps pour les trous
Nous adoptons une représentation np = np(x) et pn = pn(x) à une dimension pour un soucis de simplicité
np(x) et pn(x), s'obtiennent par la résolution des équations de continuité et d'utilisations des conditions de frontières
Considéronés l'équation de p´= Δp = (pn - pn0), c´est à dire les trous minoritaires dans la zone N




La solution mathématique s'écrit pour p´= Δp = (pn - pn0)
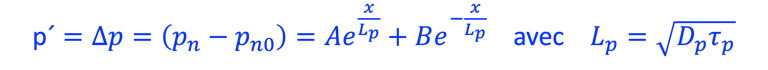
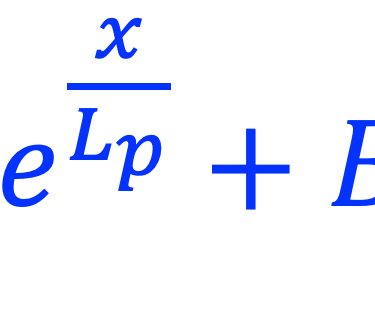
Une solution similaire peut être établie pour les électrons (minoritaires) dans la zone P
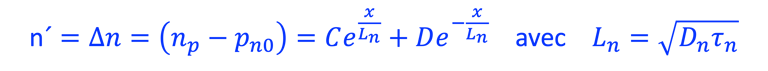
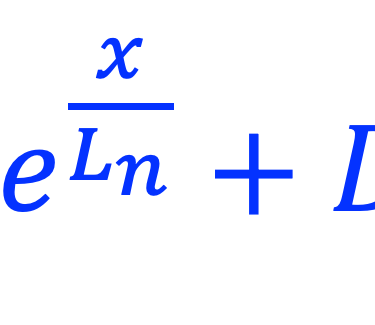
Équations de continuité et conditions aux frontières
On connait la valeur de p´(xn) à la frontière xn: p´(xn) = pn0 exp (q Va/kT)
Pour → + ∞ p´(+ ∞) est infini, alors la solution physique impose A = 0 ⇒ p´(x) = B exp (-x/Lp)
On en déduit la constante comme suit: B
à la frontière xn p´(x = xn) = B exp (-xn/Lp) = pn0 exp qVa)/kT
⇒ B = pn0 exp qVa/kT).exp (xn/Lp)
Δp = (pn - pn0) = p´(x) = B exp (-x/Lp)
Δp = [pn0 exp qVa/kT).exp (xn/Lp))] exp (-x/Lp)
pn (x) - pn0 = [pn0 exp qVa/kT).exp (xn/Lp))] exp (-x/Lp)
pn (x) - pn0 = pn0 exp qVa/kT). exp (xn/Lp))] exp (-x/Lp)
On écrit la solution pour les trous dans la zone N sous la forme:
pn (x) = pn0 [exp qVa/kT -1] exp -(x-xn)/Lp]
D'une manière similaire on écrit la solution pour les électrons dans la zone P sous la forme:
n´(x) = np0 + np0 [1-exp (qVa/kT)] exp (x+xp)/Ln)
Nous avons représenté les résultats de la résolution des équations de continuité incluant:
Le profil de concentration des porteurs de charge,
Les concentrations des porteurs minoritaires aux bords de la région de charge d'espace
Les concentrations à l'équilibre thermodynamique sont aussi représentés
Nous avons égalent illustré
l'injection des électrons et des trous
Les processus de recombinaison dans les deux zones neutres
Le profile de la densité de courant total résultant
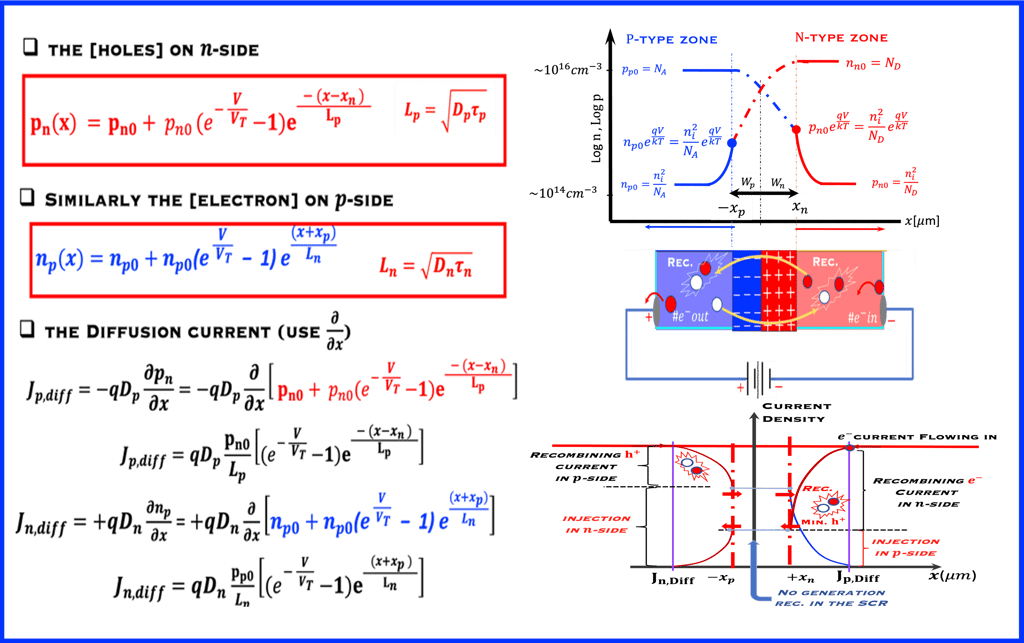
Densités de courant de diffusion total JTotal (V, T)
La dérivation des équations de pn(x) et np(x) permet d´obtenir les densités de courant: Jp = Ip/A et Jn = In/A ,
Ip et In sont les courant des trous et des electrons respectivement A étant la surface de la jonction P-N)
L'allure des courbes de densité de courants est représentées sur le tableau de gauche
La caractéristique courant tension incluant le courant inverse est représenté à droite
Le courant circule en polarisation directe et est bloqué en polarisation inverse
à la frontière x = xn et x = - xp on obtient les expression des densités de courant de diffusion des porteurs minoritaire
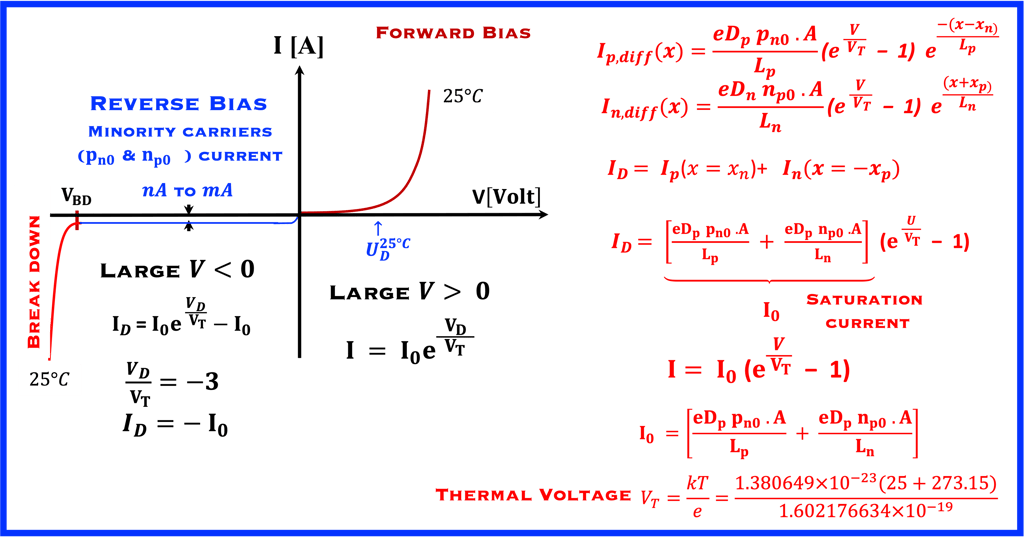
Caractéristique J(V, T, Φ) sous illumination Φ et température T
Introduction aux cellules solaire, fillière Silicium
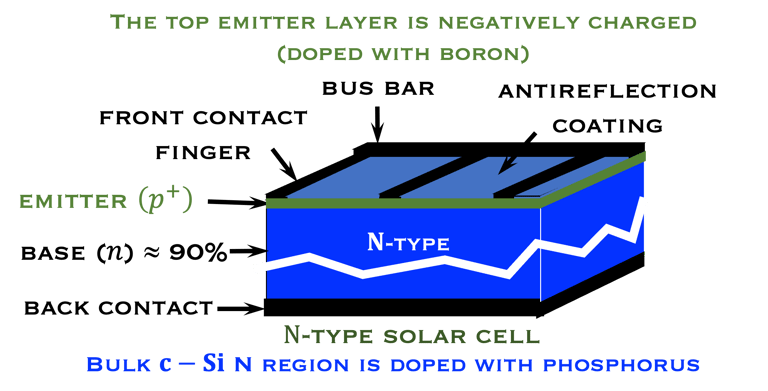

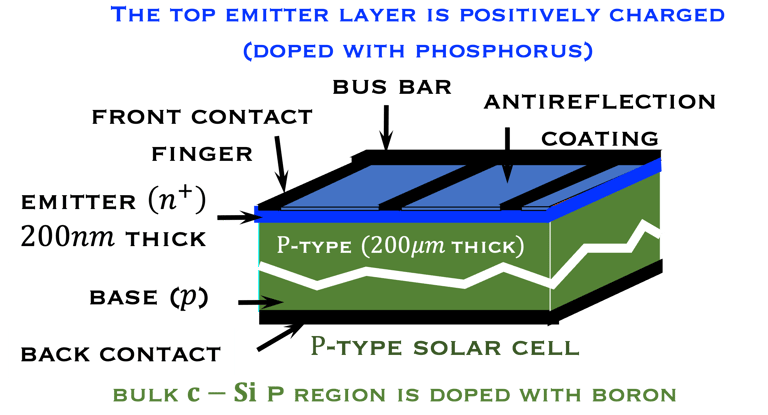
La technologie de cellules solaires la plus courante est celle du silicium caractérisées par une architecture de jonction p-n
Sur l'illustration ci-dessous on a représenté les deux zones:
L´illustration à droite représente une cellule solaire comportant:
Une zone N très fine fortement dopée négativement (épaisseur typique de 200 nm), appelé "Émetteur"
Une zone P large (épaisseur de 200-300µm) appelé "base" dopée positivement
Chaque zone va jouer un role dans la conversion de la lumière en électricité
La base, plus épaisse, généralement 90% de l'épaisseur du compostant) absorbe la majeure partie du rayonnement
L'émetteur, minimise les pertes dues à la résistance ohmique. et réduit la recombinaison des paires électron-trou
Dans la figure gauche les rôles de "Émetteur" et de la "base" sont inversés
Nous étudions chaque type P ou N de cellules solaire de la filière Si dans la partie technologie du silicium
Équation de continuité de la la jonction PN sous éclairement
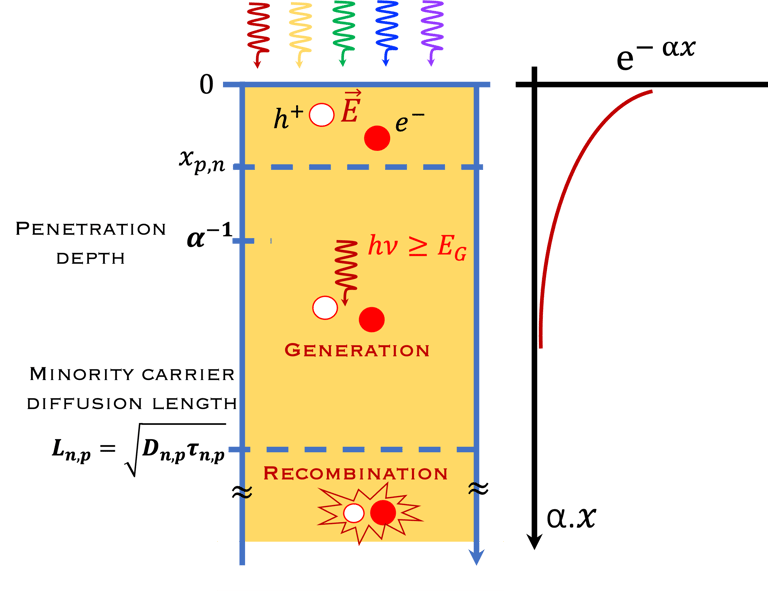
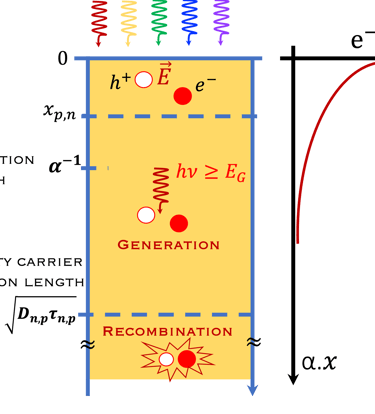
Nous considérons la face avant de la jonctions PN sous éclairement par une lumière d´énergie hc/λ ≥ EG
Les paires électron-trou sont générées sur une profondeure égale au coefficient d'absorption (1/α)
Pour garantir un déplacement des porteurs de charge jusqu'à la jonction PN
La longueur de diffusion électrons dans la zone P (Ln), et les trous dans la zone N (Lp) >> 1/α
Envisageons le cas de la region N (par exemple la cellule solaire de gauche)
Région N signifie: les électrons sont majoritaires, et les trous minoritaires
Sous l'effet de la lumière: on aura un régime permanent avec les concentrations (n + Δn) et (p + Δp)
La concentration des porteurs majoritaires (n) ne change pas de manière significative
La concentration des porteurs minoritaires augmente fortement
La collection est limité par la diffusion des porteurs minoritaires Lp
L´essentiel de l´absorption s´éffectue dans la base N
Le flux lumineux qui atteint la profondeur x s'écrit: Φ = Φ0 (1-R) exp (-αx)
Le terme (1-R) permet de tenir compte uniquement des photons qui ne sont pas réfléchis
Le flux absorbé entre x et x + dx est: dΦ = dx α (1-R) Φ0 exp (-αx)
Le nombre de paires "Electron-Trou" créé par unité de surface entre x et x +dx est:
g(x)dx = [α (1-R) Φ0 exp (-αx)/(hc/λ)] dx où g(x) est en unité [centimètre cube . seconde]
hν = hc/λ est l'énergie de création d'une paire "Electron-Trou"
Le champ électrique est nul le long des régions neutres en hors la zone de charge d’espace
La densité des trous Δp (photo)générés est solution de l´équations de continuité
C'est une équation différentielle du second degré avec une fonction de x au second membre
La solution de cette équation différentielle du second degré avec second membre s'écrit tenant compte de la valeur de B
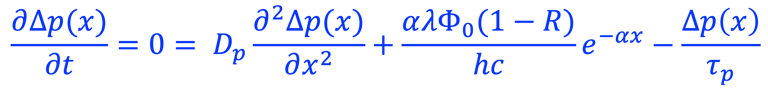
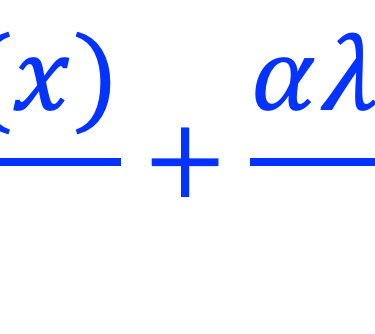
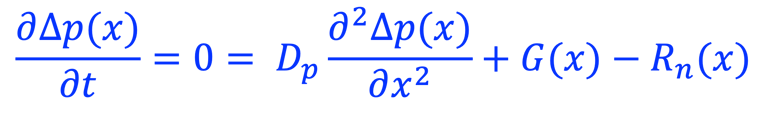
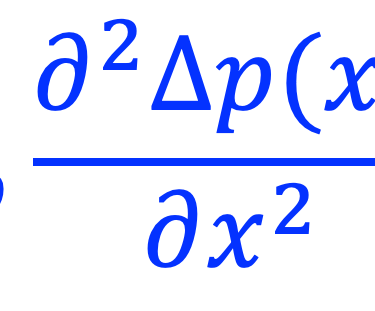
La solution sans second membre est: Δp = A exp (-x/Lp) où A est une constante d'intégration
Pour x et 1/α >> Lp il n´y a plus de trous en excès et Δp → 0
Une solution particulière est Δp = B exp (-αx)
On introduit cette solution dans l'équation de continuité et en déduit la condition sur la constante B
La solution final s'obtient on calculant la constante A: avec la condition:
x = xn ; Δp = A exp (-xn/Lp) + B exp (-αx) = 0
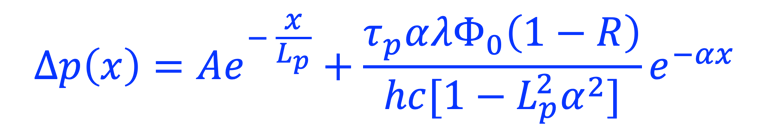
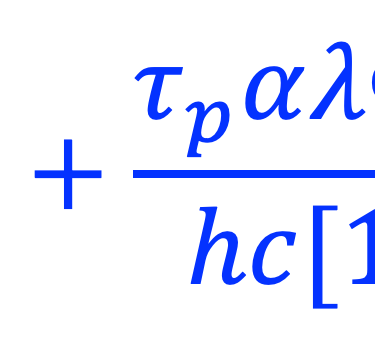
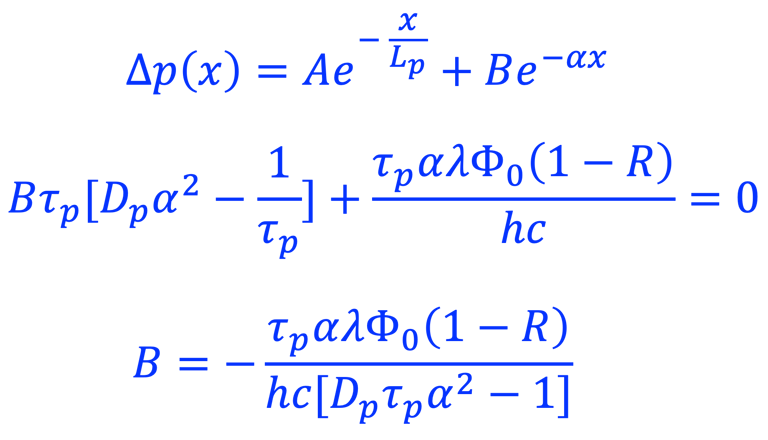
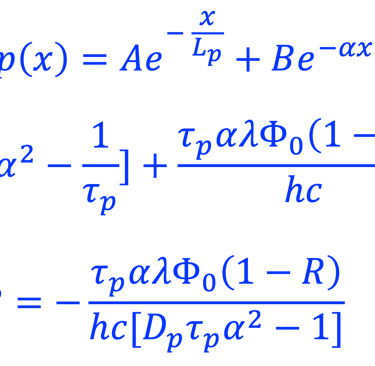
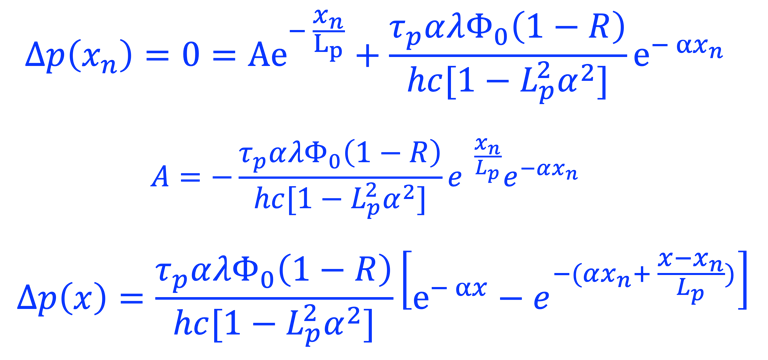
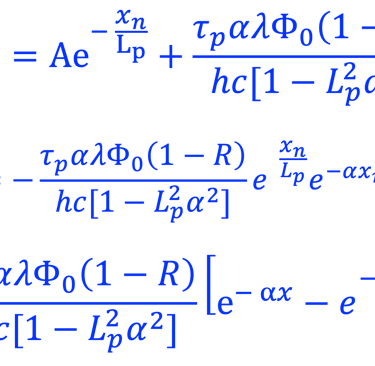
Le courant de diffusion des trous (photo)générés est donnée par:
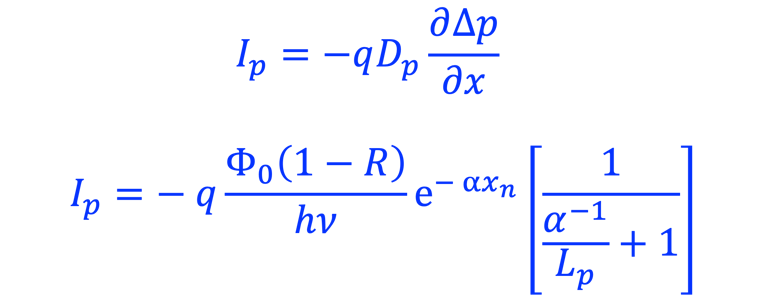
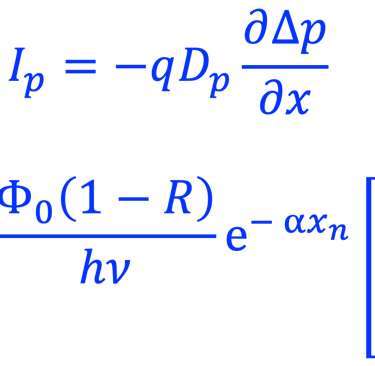
Un raisonnement similaire peut se faire pour les électrons Δn (photo)générés
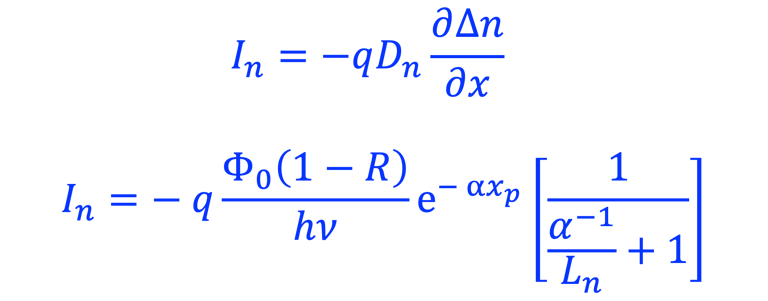
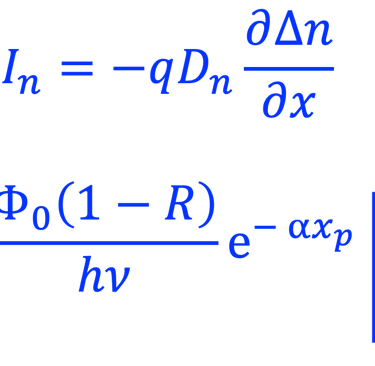
Caractéristique J(V) dans le noir and sous illumination
La figure ci-dessous illustre
Le schéma électrique équivalent qui comprend
Une générateur de courant en parallèle avec une diode
L´ensemble est connecté à résistance de charge Rload
La formulation de I(V) dans le noir comprend
- Le courant de saturation I0 qui dépend de ND, NA, Ln, Lp
- I0 dépend de manière complexe de la température
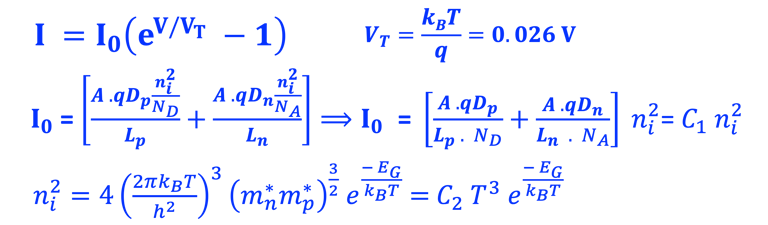
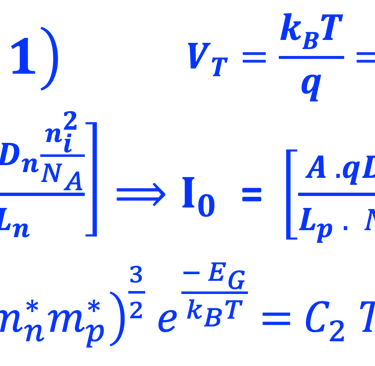
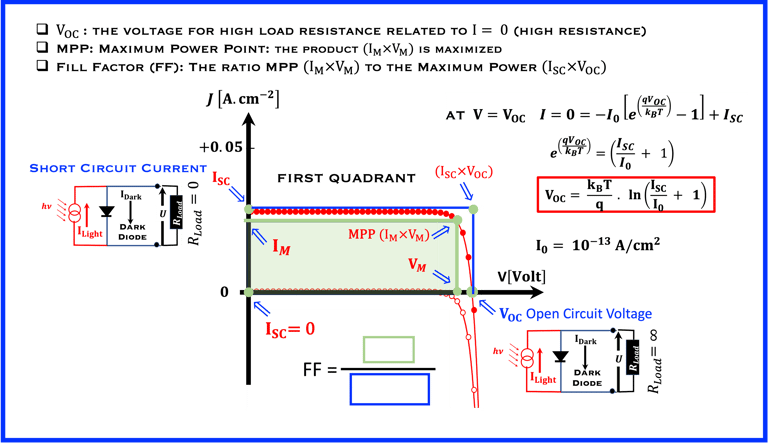
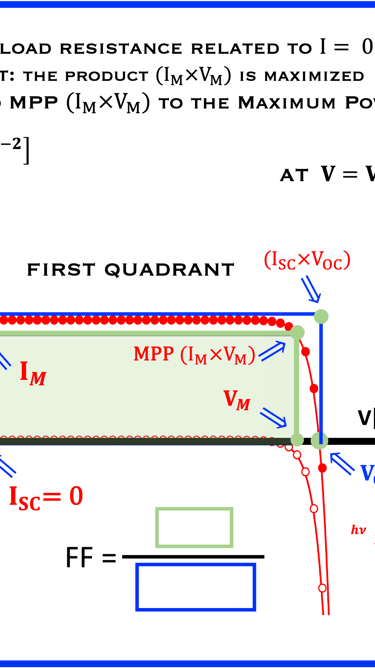
Les paramètres de la caractéristique I(V) sous clairement (cellule solaire sous radiation AM1.5, 100 mW/cm²)
ISC: Courant de court circuit, lorsque la différence de potentiel aux bornes de la jonction est neutralisée (RLoad = 0)
VOC: Potentiel de circuit ouvert (open circuit Voltage) correspondant à (Rch = ∞)
FF: facteur de forme ou "Fill Factor", il traduit le pourcentage "(IM x UM)/(ISC x VOC)" (voir l'illustration de gauche)
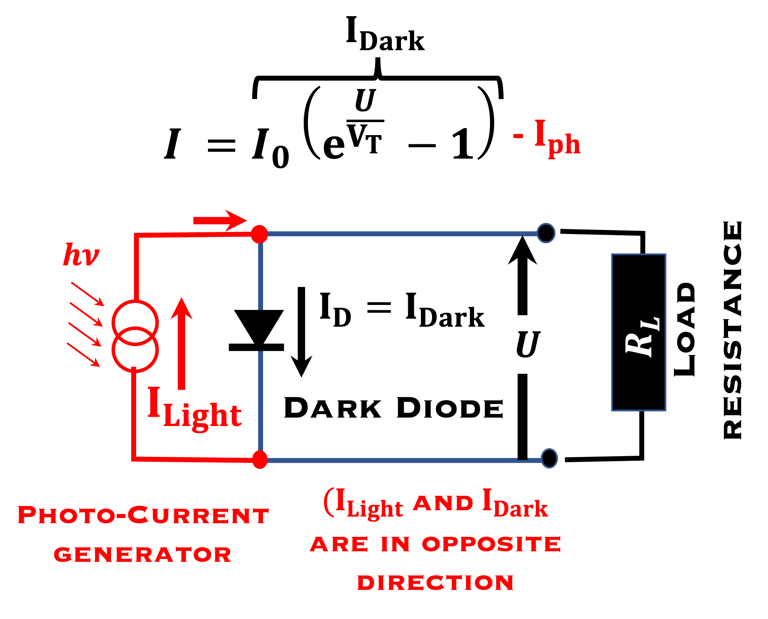
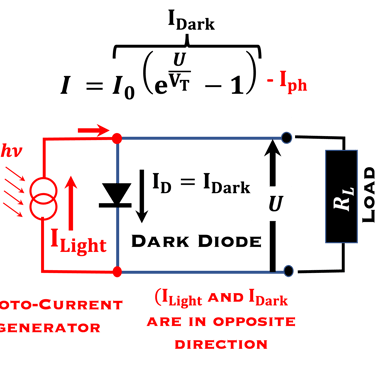
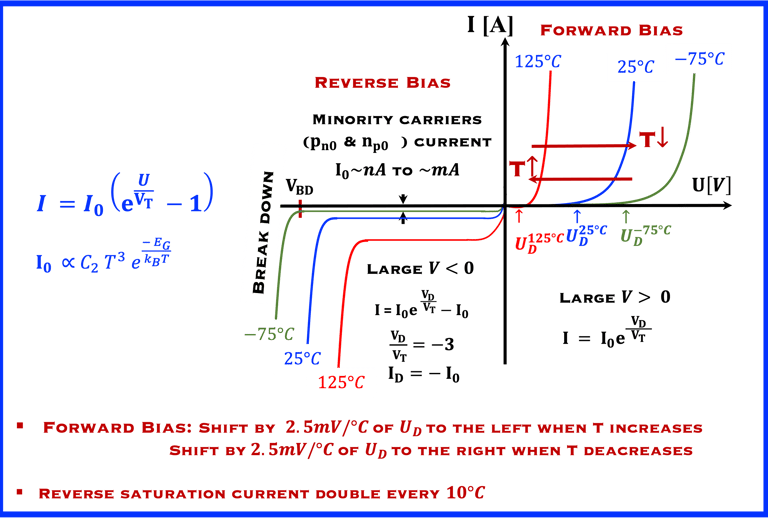
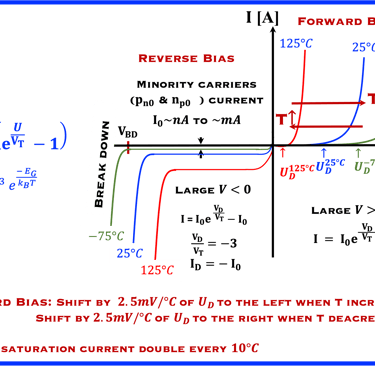
Les éléments suivant sont essentiels pour l'analyse de J(V,T)
I0 est fortement dépendant de la température
ISC est dépendant très lègerement de la température
VOC dépend d'une manière complexe de T
Les measures de I(V,T) en fonction de la température permettront de déterminer d'important paramètres tels que le courant de saturation I0, l'énergie d'activation, et d'autres paramètres essentiels pour concevoir des cellules solaires
Schéma équivalent à une diode et à deux diodes comportant une source de courant IL, une résistance série RS et une résistance parallèle RP
Les lois de Kirchhoff permettent d'établir L'équation du schéma équivalent de la jonction PN
Le modèle simplifié, décrit la caractéristique J(V) idéale de la cellule solaire basée sur une jonction PN
Le modèle contient trois termes
Le premier terme décrit la jonction PN dans le noir (ID)
Le second terme décrit le courant des porteurs minoritaires (photo)générés (IL)
Le circuit équivalent fournit des informations essentielles pour construire des cellules solaires efficaces
Le courant perdu à cause de la résistance de shunt (courant de fuite)
Ainsi le courant total est I = IL - ID - ISH
Le circuit équivalent comprend la résistance en série et la résistance en parallèle au générateur de courant


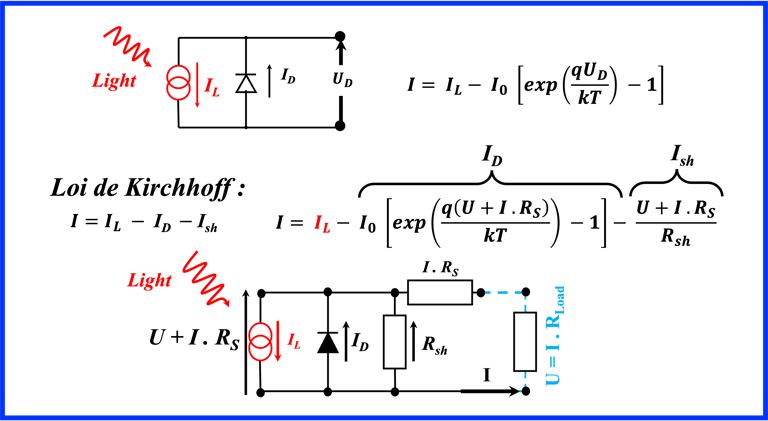
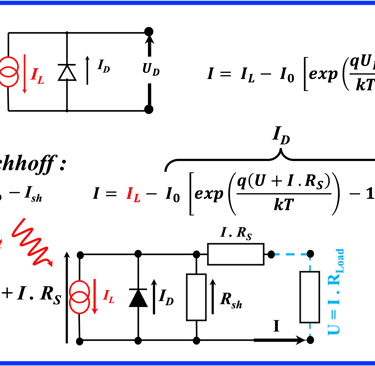
Modèle à deux diodes
Comme c´est illustrée par le circuit équivalent, le concept de deux diodes décrit séparèment:
On retrouve la diode de diffusion due aux recombinaisons des porteurs minoritaires dans le volume de la jonction PN
Auquel il faut ajouté une diode de recombinaison dans la charge d´espace
Par ailleurs on tient compte du fait que RS diminue la tension à la jonction PN et que Rp diminue le courant au niveau des diodes
J01 est la densité de courant de saturation de diffusion et J02 est la densité de courant de saturation de recombinaison
Le facteur d'idéalité n du terme de courant de recombinaison (n = 2 dans la théorie SRH pour un niveau intermédiaire)
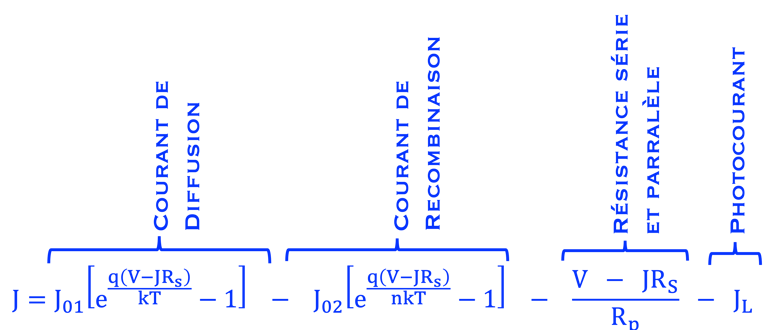
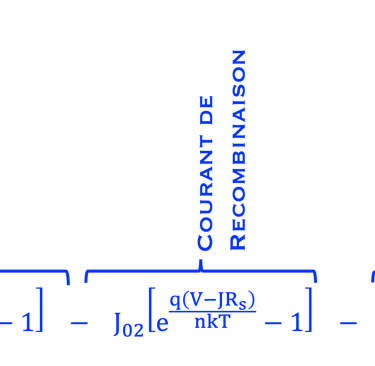
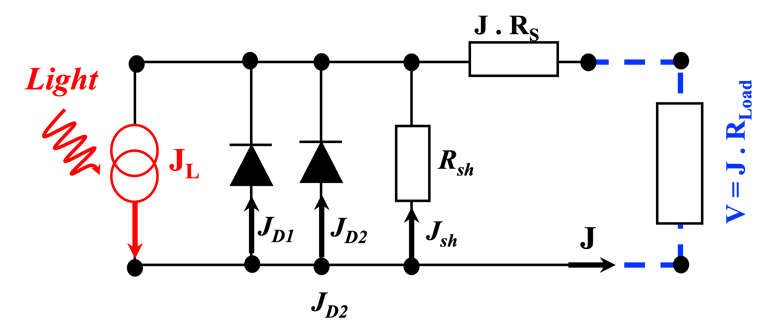
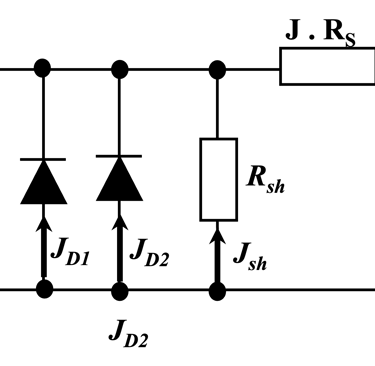
Recombinaison et durée de vie des porteurs de charges
Un état hors d'équilibre thermodynamique est caractérisé par un excès de de porteurs de charge Δn et Δp des électrons et des trous respectivement avec n = (nn0 + Δn) et p = (pn0 + Δp)
Un état hors d'équilibre peut se produire sous l'action de causes aussi bien intérieures qu'extérieures comme (température, courant électrique excitation lumineuse appropriée)
Le retour à l'équilibre par recombinaison des porteurs (électrons et trous) s'effectue en un temps caractéristique τ
On Processus de génération thermique (Gth): L'énergie thermique permet à un électron de la BV d'effectuer une transition ascendante vers la BC, laissant un trou dans la bande de valence
L’équilibre, dans un semi-conducteur, il se produit à chaque instant, et dépendant de la température, un électron peut quitter la bande de valence laissant un trou et en même temps une paires électron-trou se se recombine
On note (Gth) le taux de génération thermique, i.e. un électron de la BV qui effectue une transition ascendante vers la BC, laissant un trou dans la bande de valence
On note (GRec) le processus de recombinaison, i.e. un électron qui effectue une transition descendante de la BC vers la BV avec une certaine probabilité, et se recombine avec un trou de la BV
Le taux de recombinaison (R) est proportionnel au nombre d'électrons disponibles dans la BC et le nombre de trous dans la BV: R = B n . p , où B est est une constante de proportionnalité
Afin de maintenir l´équilibre thermique on Gth = Rth = B nn0 . pn0
nn0 et pp0 constante représentent les densités d'électrons et de trous dans le matériau de te type N
La génération (GL) par la lumière , de paires "électron-trou" en exposant la jonction PN à un flux de photon Φ dont l'énergie hc/λ >> EG (EG est le gap du matériau, pour le silicium EG = 1.1 eV) est d'une grande importance
Dans ce cas les concentrations d´électrons et de trous sont respectivement: : nn = nn0 + Δn et pn = pn0 + Δp
L'expression de la génération est G = GL + Gth
Le taux de G-R est: R = B nn pn = B (nn0 + Δn) . (pn0 + Δp)
Δn = (nn - nn0) et Δp = (pn - pn0) sont les excès de concentrations des electrons et des trous respectivement
La condition Δn = Δp permet de maintenir la neutralité des charges
Considérons l'équation de continuité pour les trous (une équation similaire peut être établie pour les électrons)
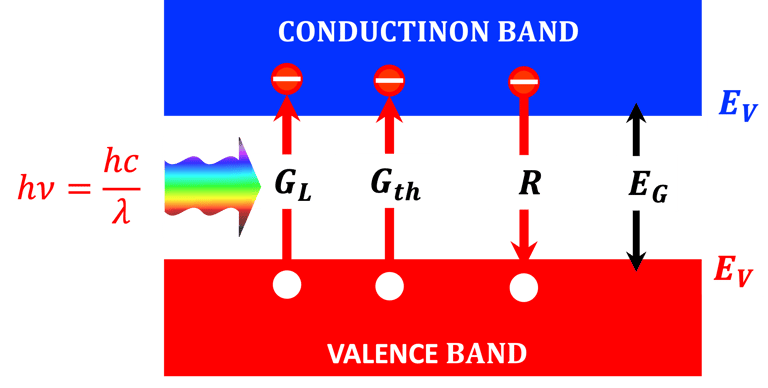
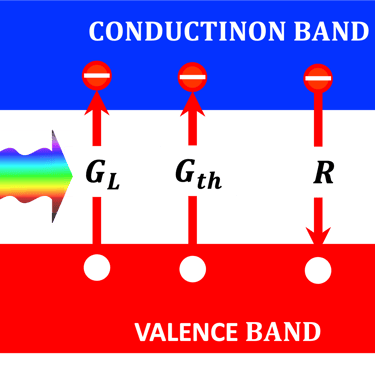

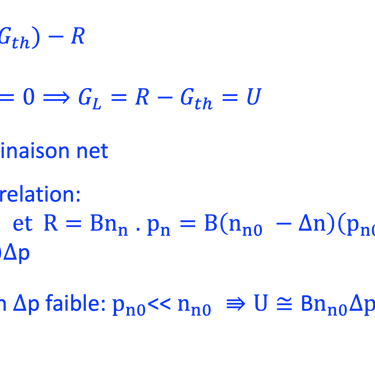
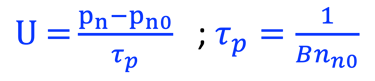
Le taux de recombinaison net est proportionnel à l'excès des porteurs minoritaires
La constante de proportionnalité 1/Bnn0 = τp est appelé "constante de temps", et c'est durée de vie moyenne des porteurs ou temps de séjour moyen d'un porteur excédentaire dans la bande de valence ou de conduction avant qu'il ne soit annihilé
Mesure de la durée de vie des porteurs minoritaires
Suite à une impulsion de lumière des paires électron-trou (porteurs minoritaires) sont crées et de déplacent par diffusion
Un photocourant transitoire de court-circuit i(t) déterminé par la collection des porteurs minoritaires
à partir du temps postérieurs à impulsion de lumière toff, on observe une décroissance décrite par une
expressions simples que Lyon édfinit comme suit:
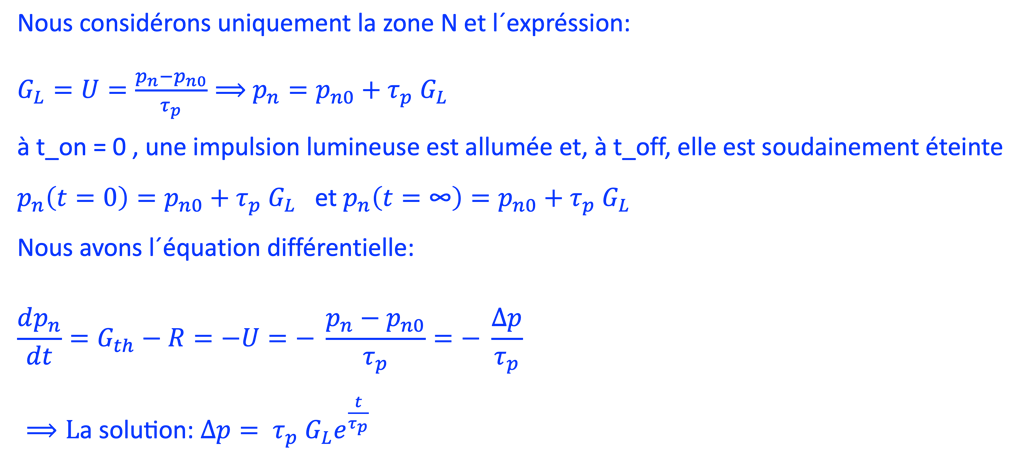
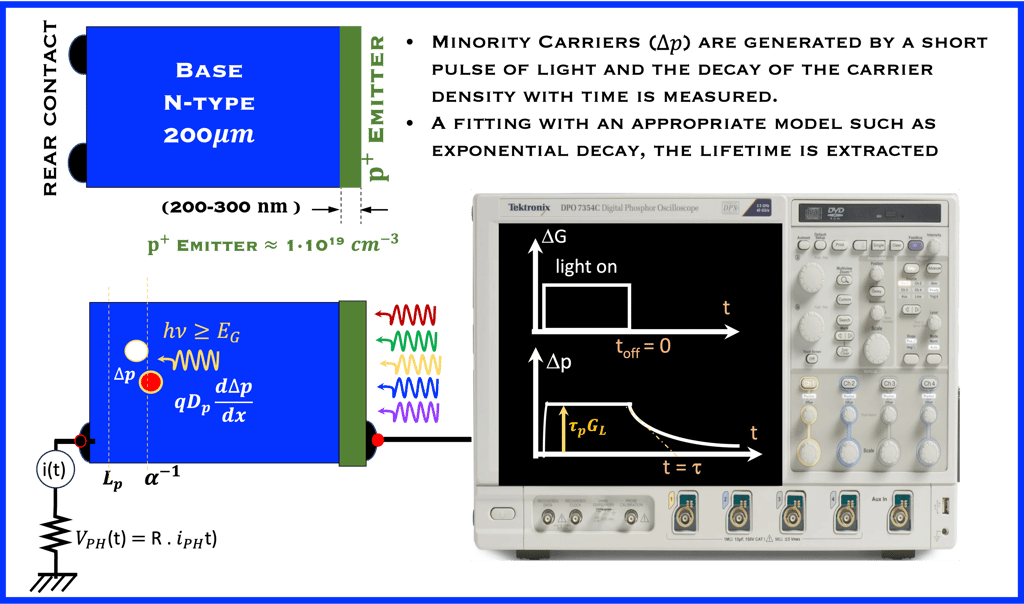
Nous avos utilisé dans l'étude de Génération-Recombinaison les références suivantes






Nous vous recommandons les cours "Vidéos" suivants




Recombinaison bande à bande radiative
Les matériaux à bande interdite directe, dans lesquels le niveau d'énergie minimal de la bande de conduction et le niveau d'énergie maximal de la bande de valence sont alignés, sont susceptibles de subir des transitions directes et une recombinaison radiative efficace (e.g. GaAs)
Dans le cas des matériaux à bande interdite indirecte, comme le silicium, la recombinaison radiative est moins dominante (voir transition direct du GaAs et indirect du Si dans l'illustration ci-dessous)

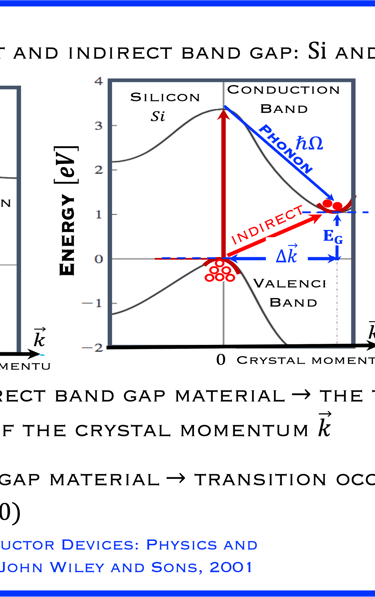
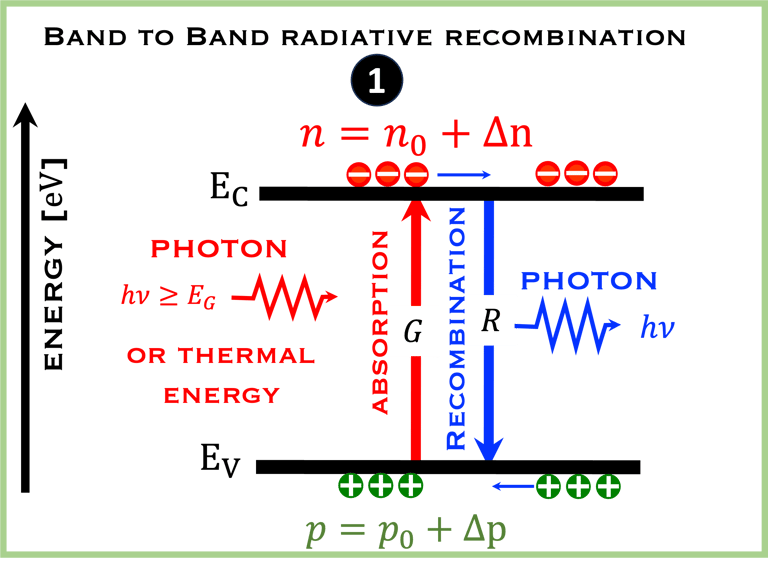
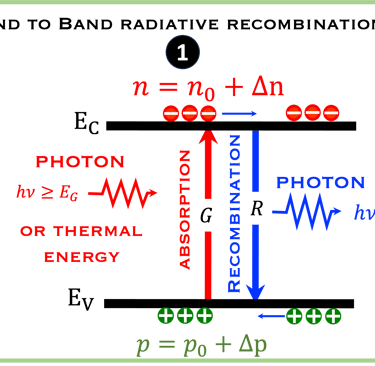
Absorption: Un électron de la bande de valence absorbe un photon et passe directement dans la bande de conduction,
Recombinaison: un électron de la bande de conduction se recombine avec un trou de la bande de valence
Au cours de cette transition, l'électron excité libère son énergie sous forme de photons, c'est-à-dire juste à l'opposé de l'énergie nécessaire pour génération de la paire électron-trou
Le taux de recombinaison radiative et la constate de temps dans les deux cas des zone N et P sont respectivement (cas de faible injection)
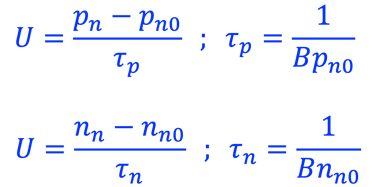

Recombinaison "Auger"
L'effet Auger est le processus où un électron de la bande de conduction (un trou de la bande de valence) excité libère l'énergie excédentaire transmise à un deuxième électron (on peut imaginer le même processus pour le trou)
Les électrons ou les trous nouvellement excités libèrent leur énergie en entrant en collision avec le réseau cristallin comme le montre l´illustration et retournent vers leur états d´équilibre
La probabilité d'une recombinaison Auger augmente avec la concentration des porteurs de charge
Les taux de recombinaison Auger et les constantes de temps pour les trous et les électrons sont:
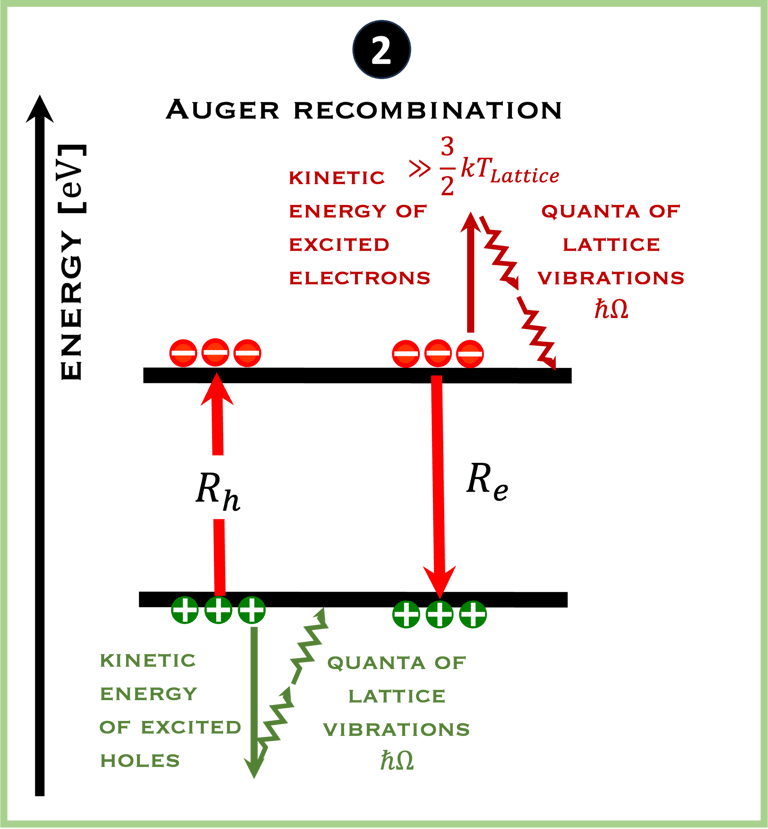
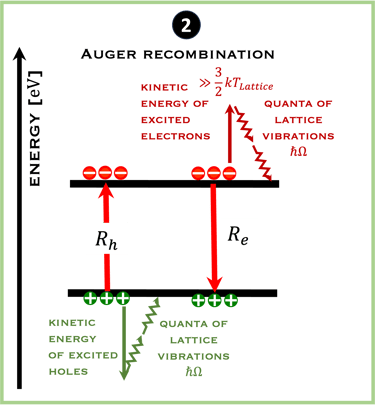


Les valeurs des coefficients Auger Cn et Cp les plus couramment citées [Thomas Dittrich/ Material Concept for Solar Cells, Energy Future Vol. 1, Imperial college press] for silicon with a doping concentration:
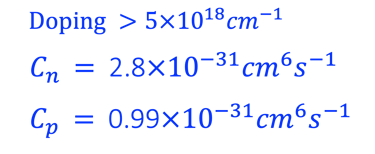
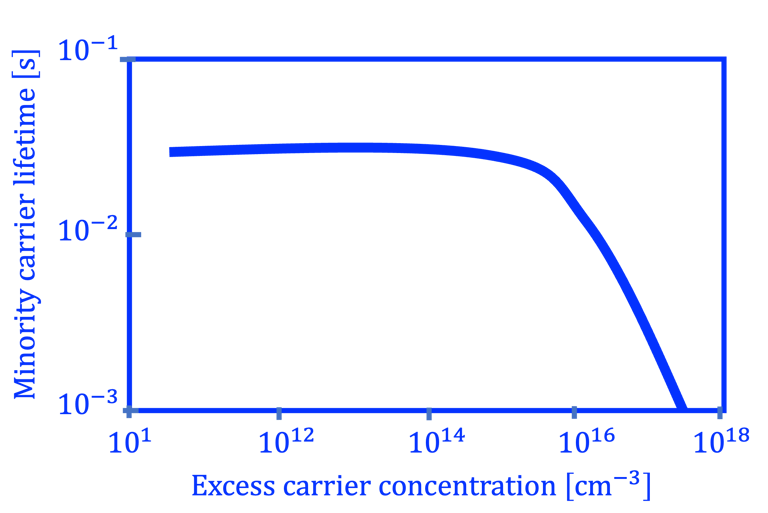
On peut représenter la durée de vie Auger en fonction de l'inverse de la densité de porteurs au carré.
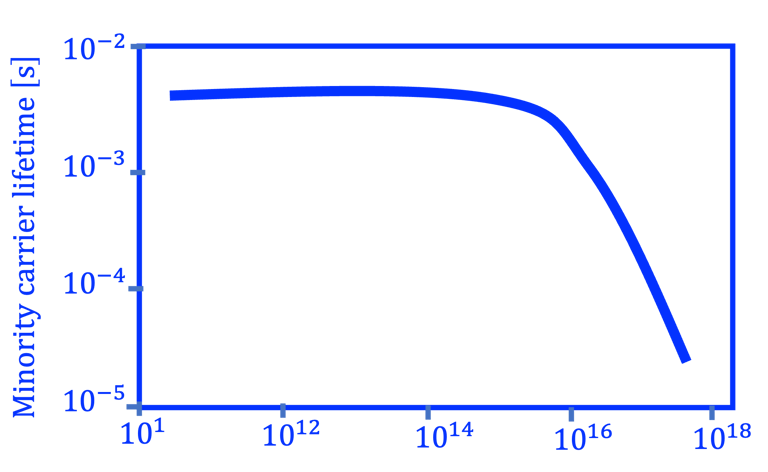
Illustration montre l'ordre de grandeur de la durée de vie des porteurs minoritaires dans la recombinaison radiative (à gauche) et la recombination Auger (à droite)
Toutes les durées de vie de recombinaison ont une valeur presque constante dans l'injection à faible niveau de porteurs, puis diminuent considérablement dans l'injection à haut niveau d'une concentration excessive de porteurs.
La recombinaison Auger est dominante dans le silicium avec des niveaux d'injection élevés, tels que les cellules solaires de laboratoire à haut rendement
Recombinaison- Génération (R-G)de Shockley-Read-Hall
ENCORE SOUS CONSTRUCTION
La recombinaison de paire électron-trou est le processus inverse de la génération, où un électron de la bande de conduction retombe dans un trou de la bande de valence qui peut se produire indirectement via le niveau intermédiaire dans ET situé dans la bande interdite (gap EG) du matériau
Ce processus de recombinaison appelé "recombinaison de Shockley-Read-Hall », acronyme (SRH) joue un rôle cruciale pour la compréhension des performances et de la fiabilité des dispositifs semi-conducteurs à cause de son impact sur la durée de vie des porteurs
Nous allons étudier les concepts d'équilibre, d'état stable et de dynamique transitoire de ce processus
On peut résumer SRH de R-G sous 4-processus, montrés sur l´illustration ci-dessous:
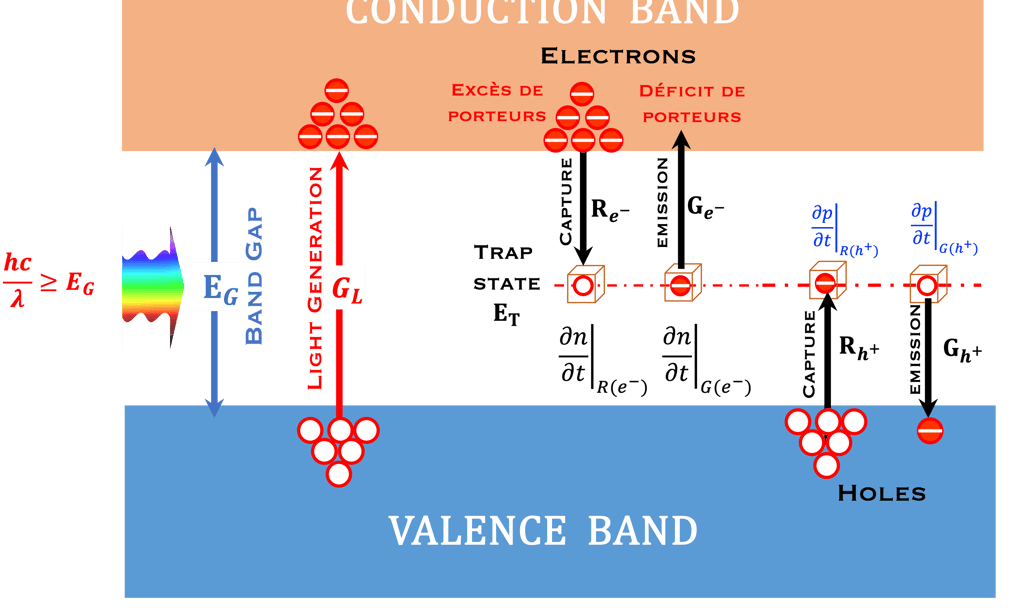
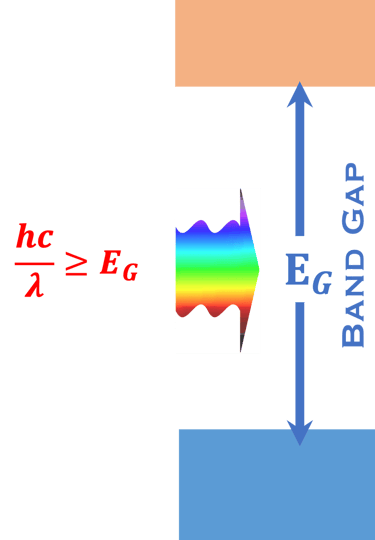


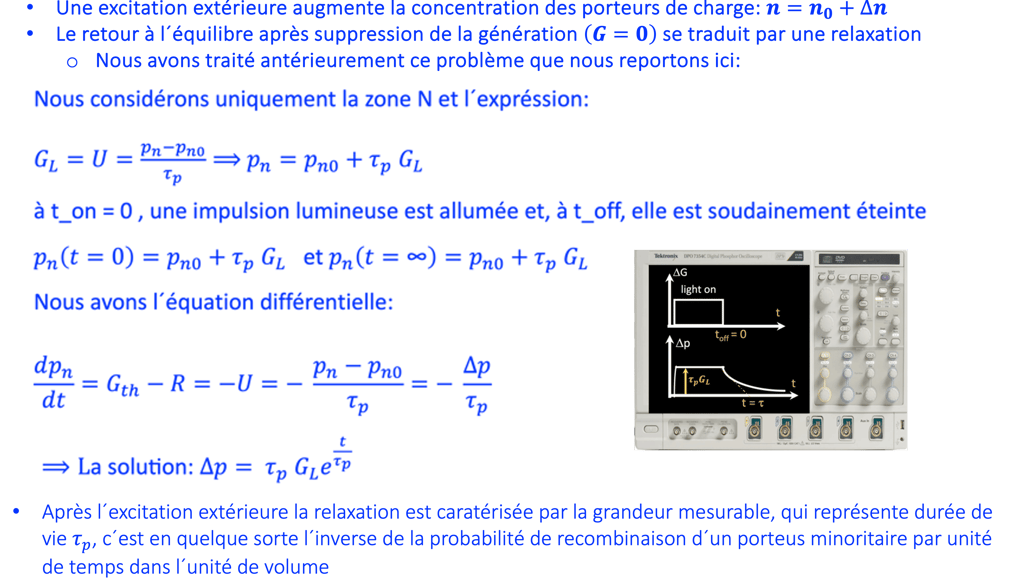

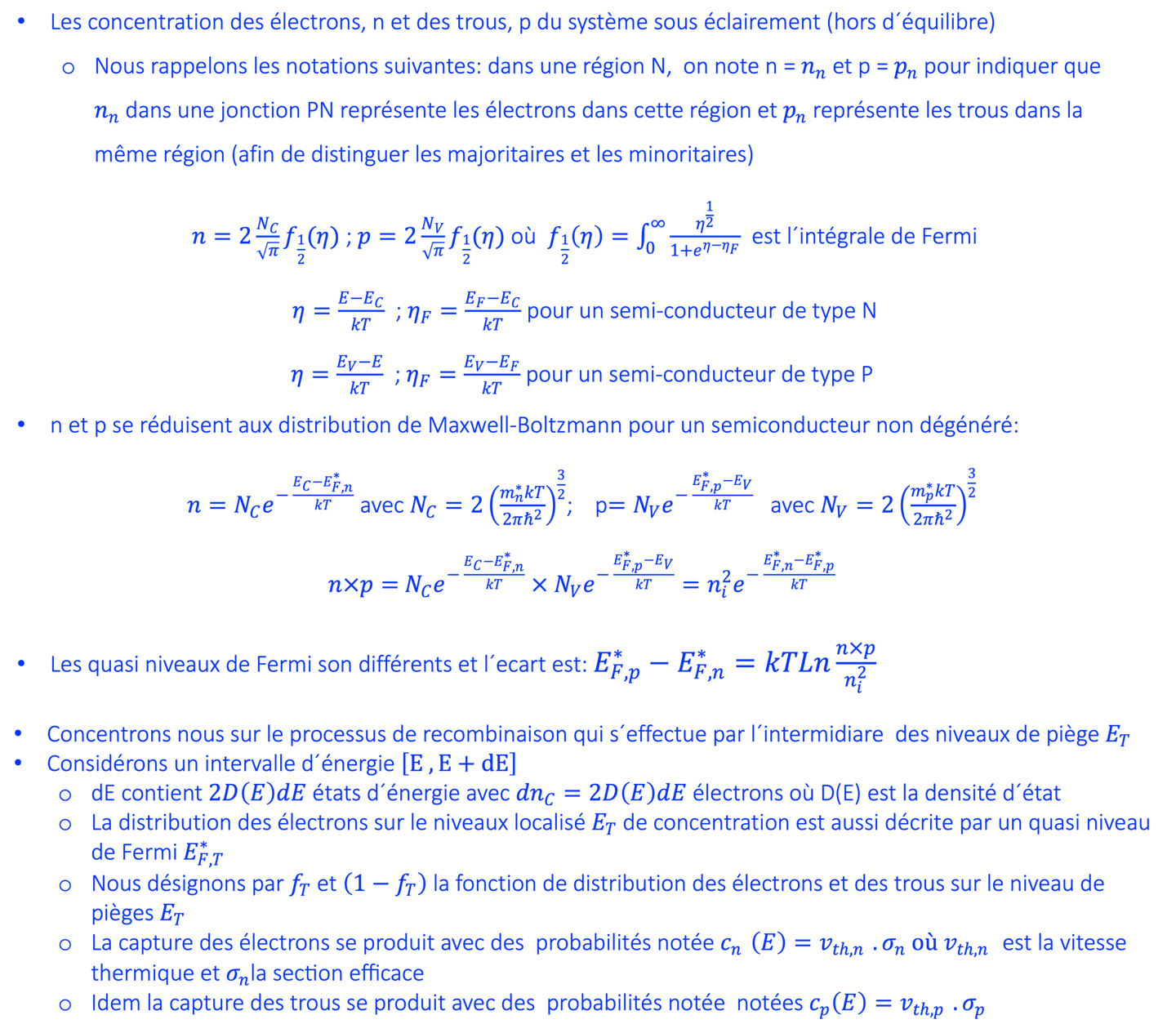



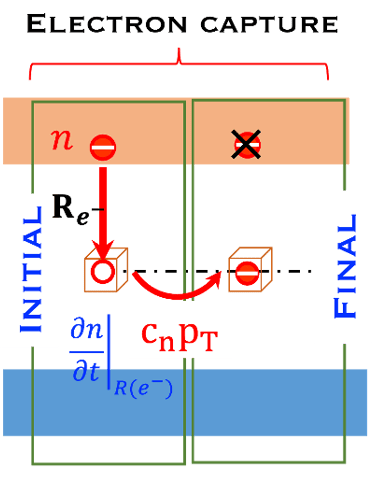
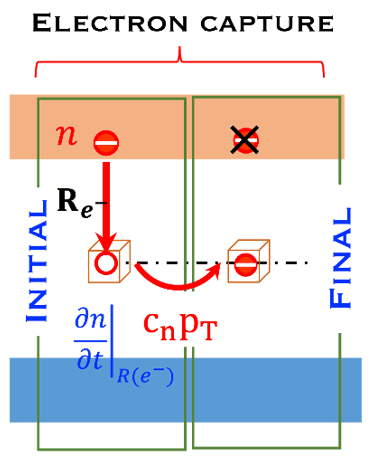
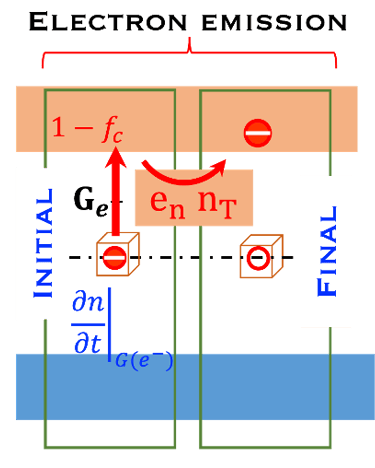

Les taux de capture ou (d´émission) des électrons (voir les deux illustrations) doit être proportionnel aux concentrations des électrons libres et à la concentration en centres de recombinaison inoccupés ou (occupés) situé au niveau de piège dans le gap d’énergie Et , donné par NT (1− FT) ou par (NTFT)
NT est la concentration totale en centres et FT est la probabilité d’occupation d’un centre piège par un électron.
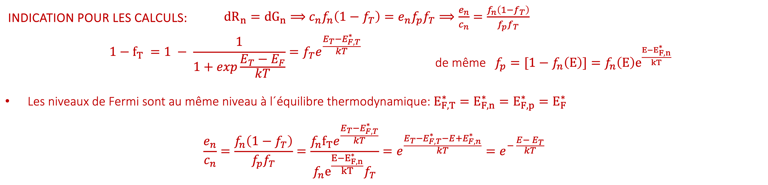
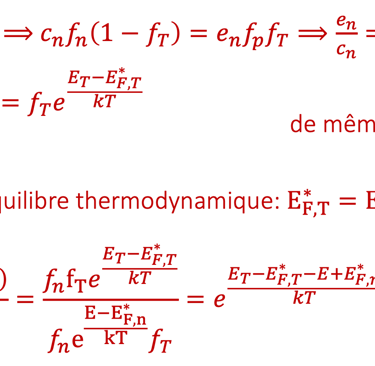


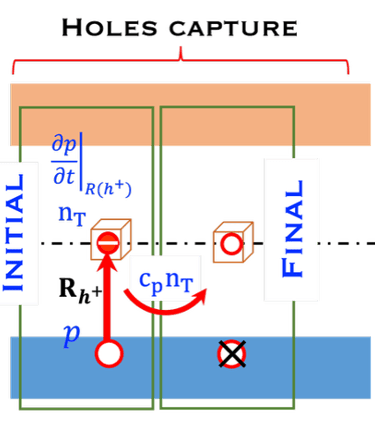

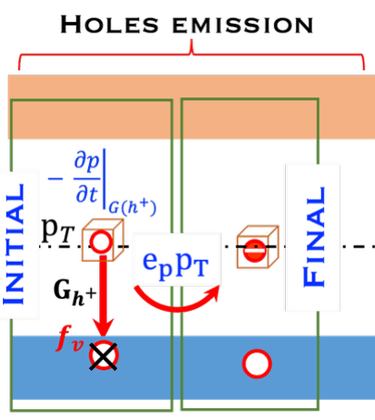
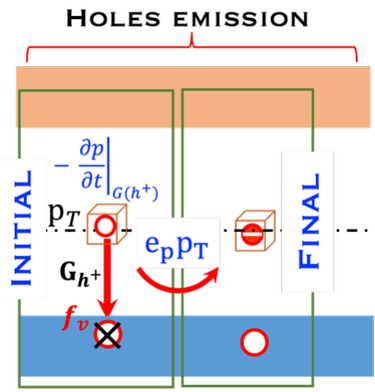
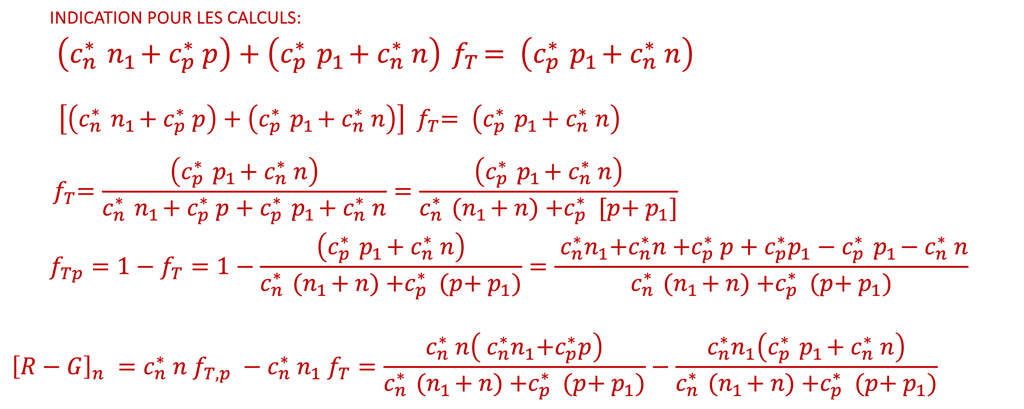

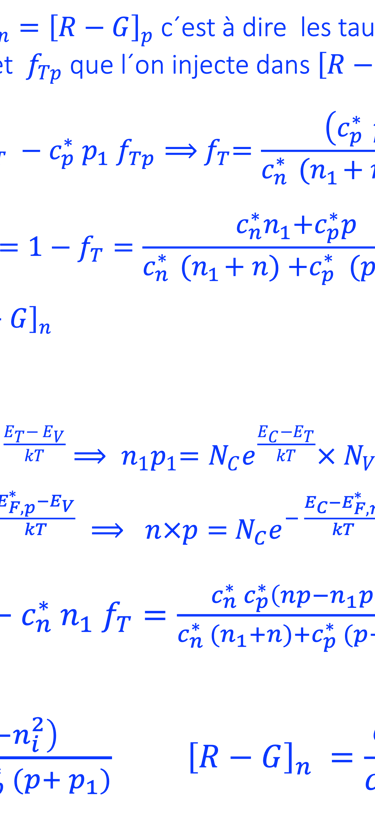
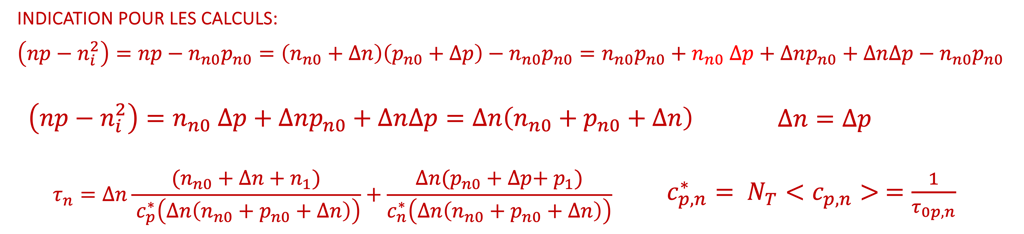
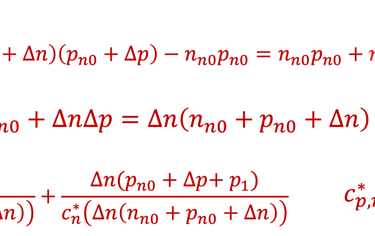
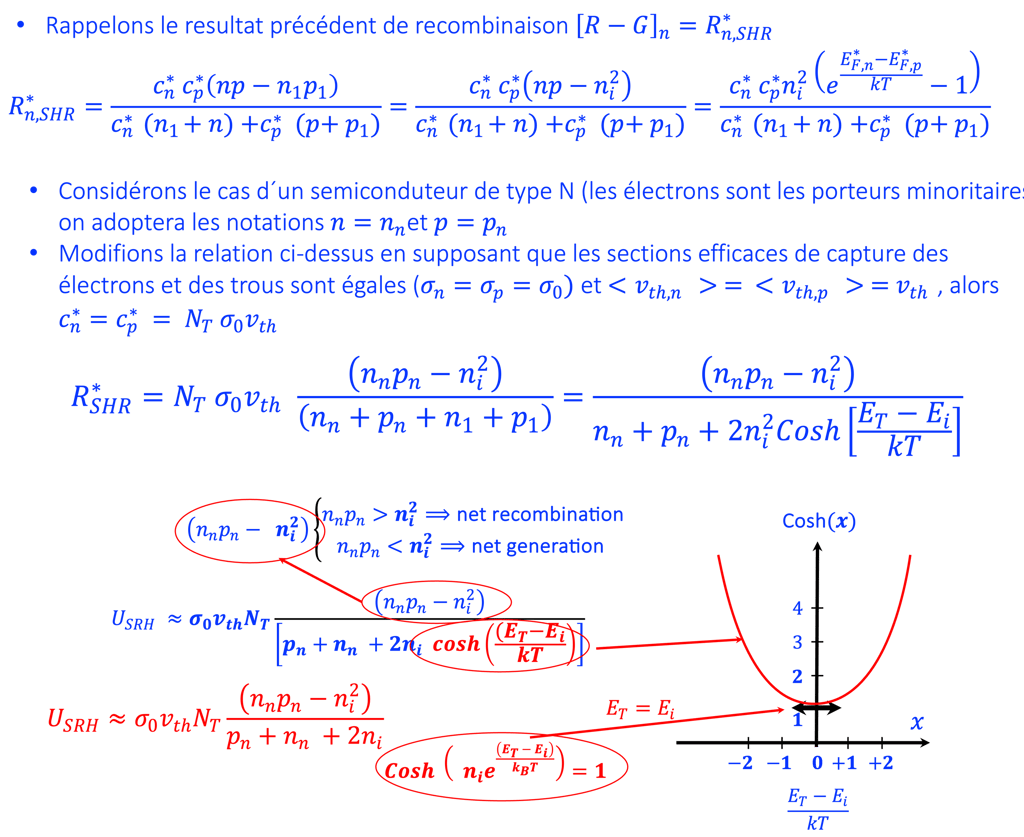
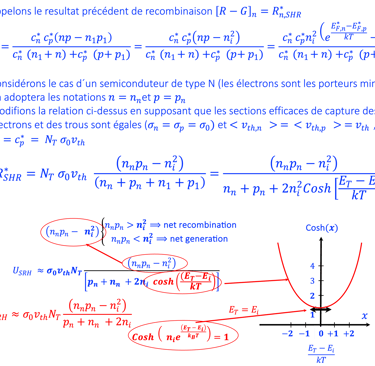




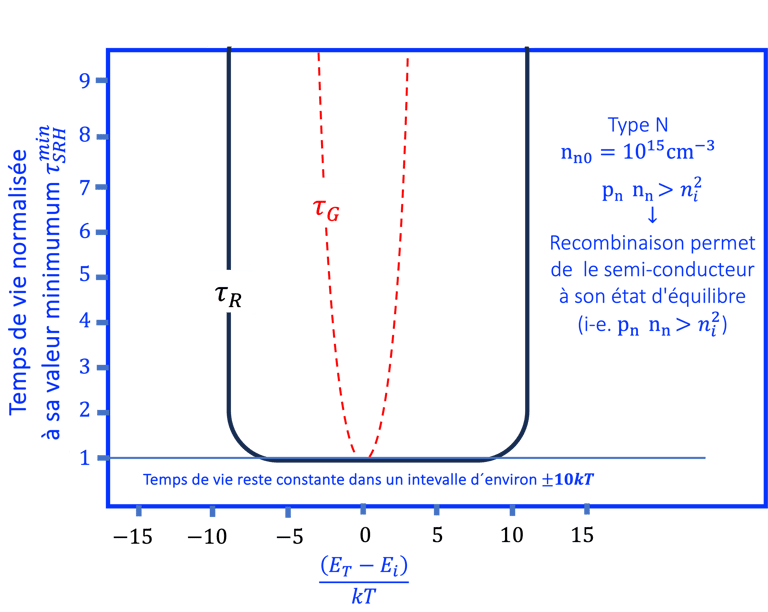






Summary / Résumé
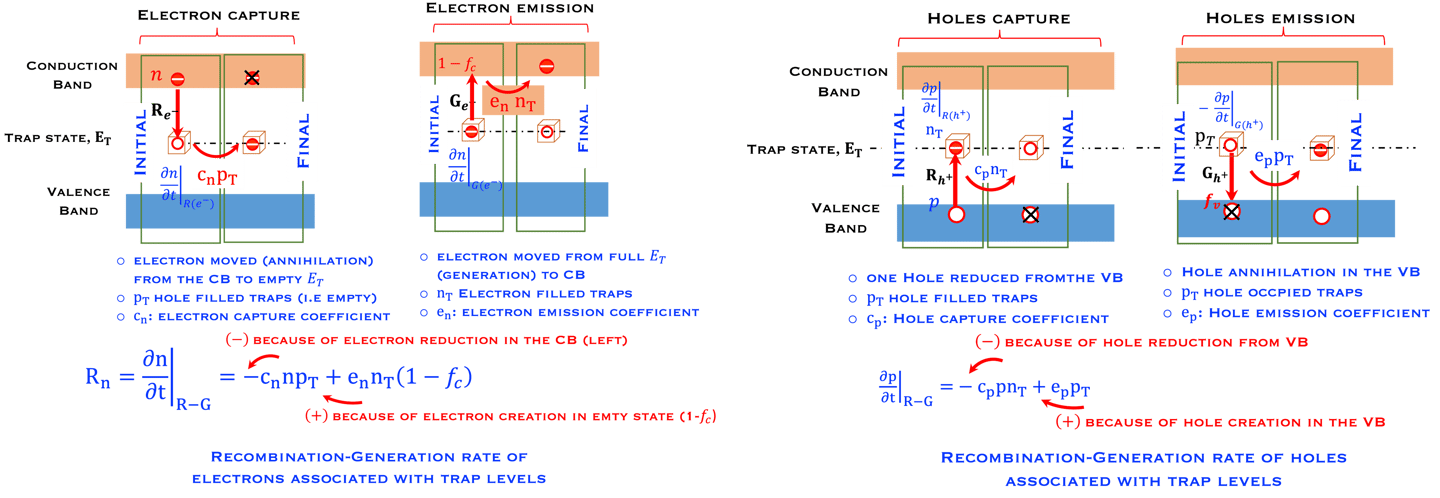
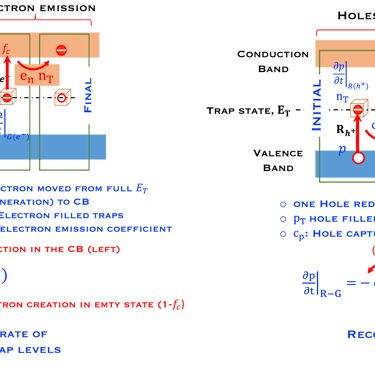
Génération et recombinaison de surface


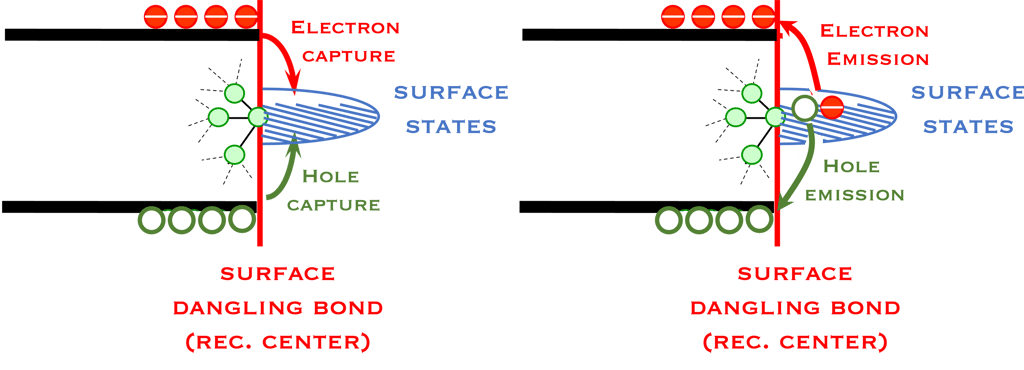
Génération et recombinaison de surface
UNDER CONSTRUCTION (Suite)
Solar Cell design
Il faut concevoir des cellules avec des résistances séries 𝑹𝒔𝒉 assez grande autant que possible et 𝑹S le plus petit possible
L'objectif est de collecter le maximum d'électrons voire améliorer la capture de la lumière
Le contact localisé a permet de réduire la résistance série et diminuer égalent les recombinaisons
Nous avons illustré le passage de la première génération "BSF" et son évolution vers PERC
Il s'agit d´inroduire des couches de passivation (e-g. Al2O3/SiNx ) et des contacts sélectives pour réduire les recombinaisons en surface, dans le volume et au contact
Les pertes résistives à cause d´une conductivité insuffisante dans le c-Si, dans les différentes couches de la cellules, et dans les métal/c-Si peuvent influencer le photocopiant et le facteur de forme (FF)
Sur l'utilisation nous avons ajouté des couches anti-réflecteurs et une texturation de surface, qui permettent de réduire la réflexivité en surface
Nous allons passer en revue plusieurs concepts tels que:
BSF (champ de surface arrière en anglais:Back Surface Field) développé par l’UNSW (University of New South Wales),
BSF est de plus en plus remplacée par la technologie "PERC" (en anglais: Passivated Emitter and Rear Cell) plus avancée qui consiste à passive avec des couches diélectriques aussi bien au niveau de l´émetteur que les contactes arrières
Les contactes ohmiques au niveau arrière (points contacte) de la technologie PERC permettent d'améliorer conductivité électrique ont un impact directe sue RS et FF
L´utilisation de couches tels que SiNx, Al2O3 améliore considérablement la réflexion interne
La particularité des couches de passivation à l'arrière de la cellule, consiste à réfléchir la lumière infrarouge qui peut éventuellement chauffer la cellule et influencer négativement VOC permettant ainsi de meilleurs performances
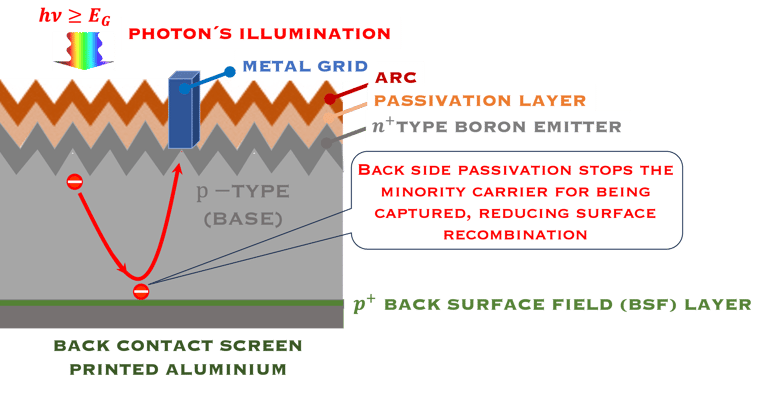
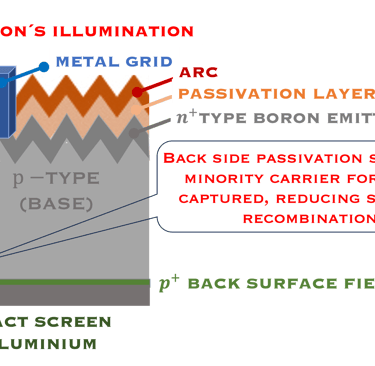
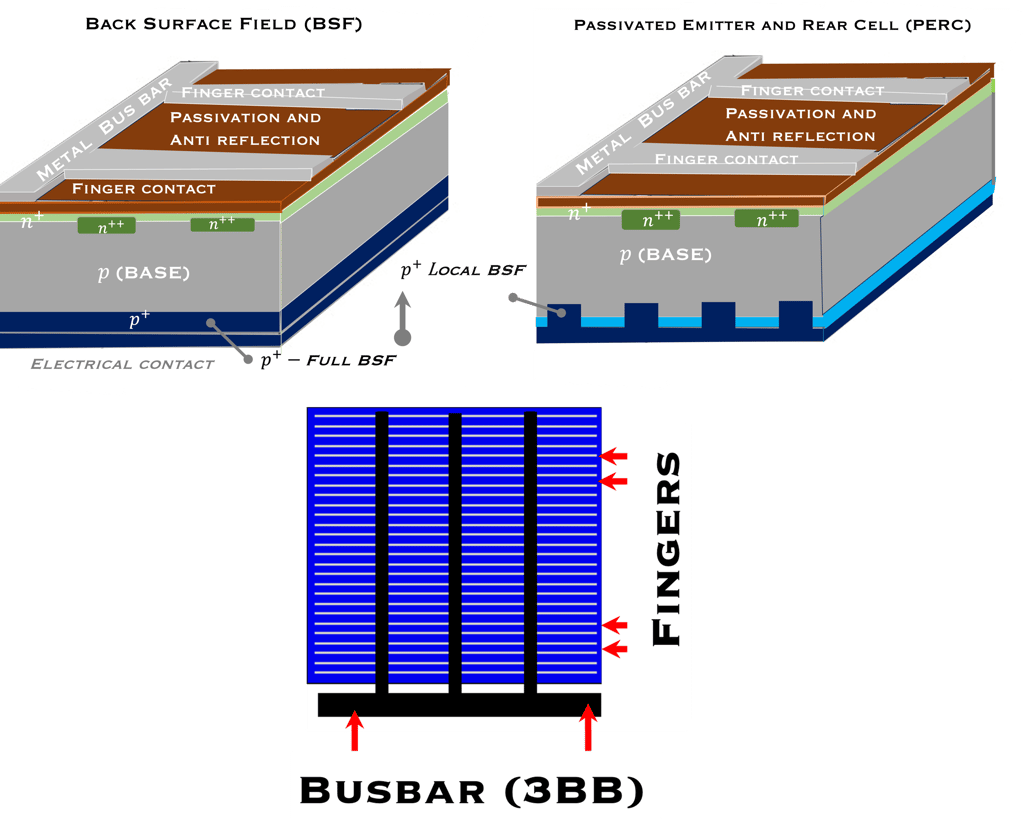
À ce niveau le lecteur doit comprendre les notions suivantes:
les bande d'énergie, le niveau de Fermi, la densité d'états dans les métaux et les semi-conducteurs,
Bande de valence et de conduction, bande interdite ou gap (directe et indirecte)
La densité d'états (DOS) des électrons et des trous,
Décrire la jonction PN, et les mécanisme physique des porteurs majoritaires et minoritaires
Jonction polarisé en direct et en inverse (jonction PN en équilibre et hors équilibre)
Équation de continuité et l'équation du courant dans une jonction P-N
Comprendre "grosso modo" les caractéristiques J(V,T, Φ)
Dans ce qui suit nous abordons les notions suivantes:
Comprendre l'aspect fondamental du dopage, de cellules solaires
Comprendre les interconnexions, revêtements antireflets, texturation de surface et techniques de passivation.
Compréhension approfondie des cellules et des modules photovoltaïques
Compréhension approfondie des courbes J(V,T, Φ), et influence de la température sur le rendement de conversion (EFF)
Compréhension et mesure expérimentales de la réponse spectrale, du rendement quantique externe et interne (EQE, IQE) et de EFF.




